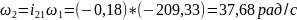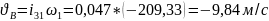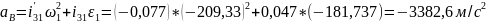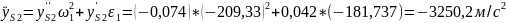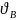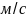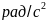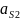- •Глава 1. Исходные данные для проектирования проектирование и исследование динамической нагруженности двс большегрузного автомобиля
- •Приложение
- •Глава 2. Блок-схема исследования динамики машинного агрегата
- •Глава 3. Динамический синтез и анализ машинного агрегата. Пункт 3.1. Задачи динамического синтеза и анализа.
- •Пункт 3.2. Структурный анализ исполнительного рычажного механизма.
- •Пункт 3.3 Определение основных размеров, масс и моментов инерции звеньев.
- •Пункт 3.4 Построение 12 планов положения механизма.
- •Пункт 3.5 Кинематический анализ механизма.
- •Подпункт 3.5.1 Графический метод кинематического анализа.
- •Подпункт 3.5.2 Аналитический метод расчета.
- •Пункт 3.6 Определение сил движущих действующих на поршень.
- •Пункт 3.7 Динамическая модель машинного агрегата.
- •Пункт 3.8 Определение приведенных моментов сил движущих и сил сопротивления.
- •Пункт 3.9 Определение переменной составляющей приведенного момента инерции
- •Пункт 3.10 Определение постоянной составляющей приведенного момента инерции и момента инерции маховика
- •Пункт 3.11 Определение закона вращения звена приведения
- •Пункт 3.12 Схема алгоритма программы исследования динамической нагруженности машинного агрегата
- •Пункт 3.13. Обработка результатов расчётов
- •Кинематические характеристики .
- •Переменная составляющая приведенного момента инерции и её слагаемые а, в, с.
- •Приведенный момент движущих сил и приведенный момент сил сопротивления .
- •Работа движущих сил и работа сил сопротивления .
- •Изменение кинетической энергии машины ∆t( и изменение кинетической энергии постоянной составляющей приведенного момента инерции ∆ .
- •Изменение угловой скорости ∆ и угловое ускорение звена приведения.
- •Пункт 3.14. Выводы
- •Глава 4. Динамический анализ рычажного механизма Пункт 4.1. Задачи динамического анализа
- •Пункт 4.2. Кинематический анализ механизма
- •Подпункт 4.2.1. Графический метод расчётов
- •Подпункт 4.2.2. Аналитический метод расчётов
- •Подпункт 4.2.3. Сопоставление расчётов
- •Пункт 4.3. Силовой расчёт
- •Подпункт 4.3.1. Графический метод расчётов
- •Подпункт 4.3.2. Аналитический метод
- •Пункт 4.4. Обработка результатов расчётов
- •Реакции и , действующие на звено 2.
- •Реакци в направляющих ползуна.
- •Годограф реакции .
- •Пункт 4.5. Выводы
- •Глава 5. Синтез кулачковых механизмов Пункт 5.1. Задачи синтеза
- •Пункт 5.2. Исходные данные для проектирования
- •Пункт 5.3. Определение кинематических характеристик
- •Пункт 5.4. Определение основных размеров кулачкового механизма
- •Пункт 5.5. Определение координат центрового профиля кулачка
- •11,69 Град.
- •Пункт 5.6. Построение графиков кинематических характеристик
- •Пункт 5.7. Построение графика угла давления
- •Пункт 5.8. Построение полной и упрощённой совмещённых диаграмм
- •Пункт 5.9. Построение центрового профиля кулачка
- •Пункт 5.10. Определение радиуса ролика и построение действительного профиля кулачка
- •Пункт 5.11. Определение жёсткости замыкающей пружины
- •Пункт 5.12. Выводы
- •Литература
Подпункт 4.2.2. Аналитический метод расчётов
Известно, что угловая скорость к-го звена равна:
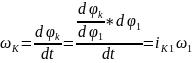 ,
,
т.е. угловая скорость к-го звена равна произведению аналога угловой скорости этого звена на угловую скорость звена приведения 1.
Аналогичные выражения можно получить для проекций скорости какой-либо точки звена (например, точки М):
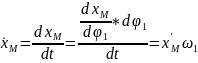 ;
;
 .
.
Угловое ускорение к-го звена:
 .
.
Так как:
 ,
,
то:
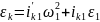 .
.
Аналогично рассуждая, получим проекции ускорения точки М:
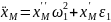 ,
,
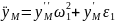 .
.
Алгоритм определения скоростей и ускорений для кривошипно ползунных механизмов имеет вид:
Модули и направления векторов абсолютной скорости и ускорения точки определяются на основании выражений:
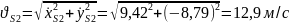 ;
;
 ;
;
 ;
;
 ;
;
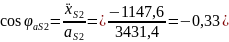 ;
;
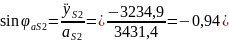 .
.
Подпункт 4.2.3. Сопоставление расчётов
Сопоставление результатов расчётов графического и аналитического методов приведено в табл. 4.1.
Таблица 4.1
Параметр |
Ед. изм. |
Графический метод |
Аналитический метод |
|
|
10 |
-9,84 |
|
|
36,7 |
37,68 |
|
|
13,2 |
12,88 |
|
|
3350 |
-3382,6 |
|
|
4593,2 |
-4436,8 |
|
|
3400 |
3441,4 |
Пункт 4.3. Силовой расчёт
При силовом расчёте механизма рассматриваются статически определимые кинематические цепи (группы Ассура), причём расчёт начинается с группы, наиболее удалённой от начального звена.
Подпункт 4.3.1. Графический метод расчётов
Определяем силы и моменты сил инерции звеньев:
 ;
;
 ;
;
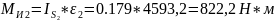 ;
;
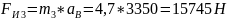 .
.
Силы инерции направлены противоположно ускорениям центров масс, а моменты сил инерции — противоположно угловым ускорениям звеньев.
Силовой
расчёт выполняется в порядке, обратном
присоединению структурных групп.
Отделяем от механизма статически
определимую структурную группу (2,3) и
прикладываем действующие силы. В точке
В приложена реакция
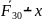 ,
а в точке А — реакция
,
а в точке А — реакция
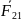 ,
которую раскладываем на нормальную
составляющую
,
которую раскладываем на нормальную
составляющую
 ,
направленную вдоль звена AB,
и тангенциальную составляющую
,
направленную вдоль звена AB,
и тангенциальную составляющую
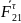 ,
направленную перпендикулярно AB.
,
направленную перпендикулярно AB.
Составляющую находим из уравнения моментов всех сил, действующих на звено 2, относительно точки B:
 или
или
 ;
;
откуда
 ;
;
Плечи
сил
 ,
,
 ,
АВ берутся непосредственно из чертежа
измерением в миллиметрах.
,
АВ берутся непосредственно из чертежа
измерением в миллиметрах.
Составляющую
,
полную реакцию
и реакцию
 находим путём построения плана сил
согласно уравнению равновесия группы,
записанному в соответствии с принципом
Даламбера:
находим путём построения плана сил
согласно уравнению равновесия группы,
записанному в соответствии с принципом
Даламбера:
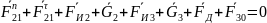 .
.
Принимаем
масштабный коэффициент сил
 и находим отрезки, изображающие все
известные силы:
и находим отрезки, изображающие все
известные силы:
 ;
;
 мм;
мм;
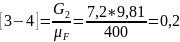 мм;
мм;
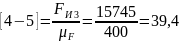 мм;
мм;
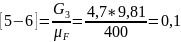 мм;
мм;
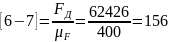 мм.
мм.
Из плана сил находим:
 Н;
Н;
 Н;
Н;
 Н.
Н.
Реакцию
 ,
действующую на звено 2 со стороны звена
3, определяем из уравнения равновесия
звена 2, используя при этом построенный
план сил группы:
,
действующую на звено 2 со стороны звена
3, определяем из уравнения равновесия
звена 2, используя при этом построенный
план сил группы:
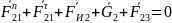 .
.
Тогда:
 Н.
Н.
Далее
рассматриваем начальное звено — кривошип
1. В точке А приложена реакция
 ,
а в точке О — реакция
,
а в точке О — реакция
 ,
которую находим путём построения плана
сил согласно уравнению равновесия:
,
которую находим путём построения плана
сил согласно уравнению равновесия:
 .
.
Масштабный
коэффициент сил
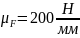 .
Отрезки, изображающие известные силы:
.
Отрезки, изображающие известные силы:
 мм;
мм;
 мм.
мм.
Тогда:
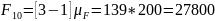 Н.
Н.
Уравновешивающий
(движущий) момент
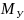 определяем из уравнения моментов всех
сил, действующих на звено 1, относительно
точкм О:
определяем из уравнения моментов всех
сил, действующих на звено 1, относительно
точкм О:
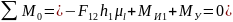 ,
,
откуда:
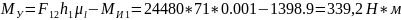 .
.