5.2. Густина розподілу наробітку до відмови

Густина розподілу наробітку до відмови або інакше диференціальний закон розподілу наробітку до відмови є похідна від імовірності відмови

. (2.3)

Тому справедливо наступне визначення. Густина розподілу наробітку до відмови ‑ це безумовна ймовірність виникнення відмови на нескінченно малому проміжку віднесена до величини цього проміжку.

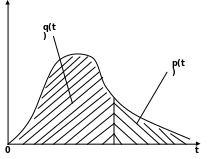
Рис. 2.3

Розмірність густини розподілу (1/одиниця часу).

З теорії ймовірностей відомо, що густина розподілу наробітку до відмови має наступні властивості:

1)  ;

2)  .

Через густину імовірності і можна виразити (рис. 2.3) так:

.

Статистичну оцінку густини розподілу знаходять по формулі

, (2.4)

де – дискретні значення наробітку, кратні .

Скориставшись формулою (2.2), можна одержати

, (2.5)

де  ‑ число об'єктів, які відмовили в проміжку наробітку .

5.3. Інтенсивність відмов

Згідно ДСТУ 2860-94 інтенсивність відмов – це умовна густина ймовірності виникнення відмови об'єкта, яка визначається за умови, що до цього моменту часу відмова не виникла.

Відповідно до цього визначення

(2.6)

Проінтегрувавши останню рівність, отримаємо

,

Звідки:

(2.7)

Цей важливий вираз іноді називають узагальненим законом надійності.

Умовна ймовірність безвідмовної роботи протягом наробітку , знайдена з припущення, що при об'єкт був працездатним, визначається з урахуванням виразу (2.7) за формулою

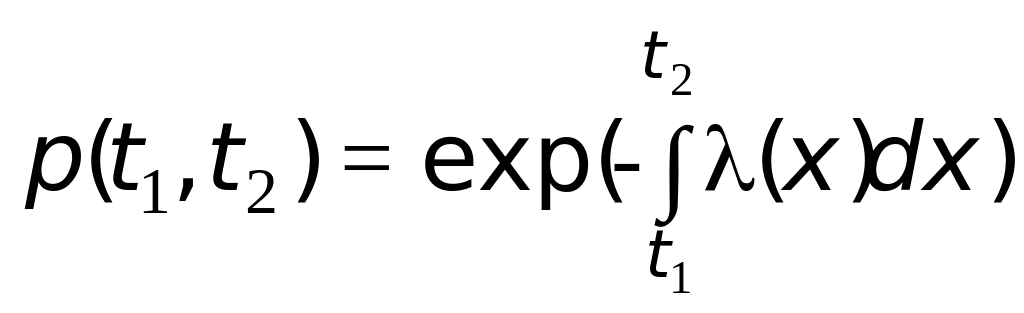
Скориставшись рівністю (2.7), через інтенсивність відмов можна показати також густина розподілу наробітку до відмови:

(2.9)

Вираз для статистичної оцінки інтенсивності відмов можна одержати, застосувавши формулу (2.6):

(2.10)

Підставивши у формулу (2.10), отримані раніше вирази для і знаходимо

(2.11)

Необхідно ясно розуміти відмінність між густиною і інтенсивністю . Так елемент імовірності є безумовна ймовірність відмови об'єкта на проміжку , а елемент імовірності – це умовна ймовірність відмови об'єкта в проміжку за умови, що до моменту об'єкт був справним. Таким чином, при і при . Зразковий вид функцій і показаний на рис. 2.4.

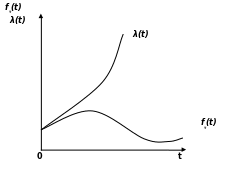
Рис 2.4.

Це розходження добре видно також з формул (2.5) і (2.11) для статистичних оцінок. Оцінка відповідно до формули (2.5) визначається як відношення числа об'єктів, що відмовили, в одиницю часу до кількості всіх об'єктів, поставлених на випробування, а - оцінка відповідно до формули (2.11) – як відношення того ж числа об'єктів, що відмовили, кількості об'єктів, що залишилися справними до моменту часу .

5.4. Середній наробіток між відмовами

Відповідно ДСТУ 2860-94 середній наробіток між відмовами – це відношення сумарного наробітку відновлюваного об’єкта до математичного сподівання числа його відмов протягом цього наробітку.

Відповідно до цього визначення

, (2.12)

де – символ математичного сподівання.

Величину можна також виразити через імовірність безвідмовної роботи . Провівши інтегрування за частинами, із виразу (2.12) отримаємо

.

У цьому виразі перший доданок дорівнює нулю, тому що , а при імовірність наближається до нуля швидше, ніж зростає . Отже,

(2.13)

Таким чином, середній наробіток до відмови чисельно дорівнює площі, обмеженої кривою і віссю абсцис.

Статистична оцінка середнього наробітку до відмови визначається як середнє арифметичне:

, (2.14)

де – наробіток до відмови i-го об'єкта ( ).