Кількісні показники надійності

Властивості	Позначення показників	Найменування показників
Безвідмовність		Імовірність безвідмовної роботи Густина розподілу наробітку до відмови Середній наробіток до відмови Інтенсивність відмов Параметр потоку відмов Середній наробіток на відмову
Ремонтопридатність		Імовірність відновлення в заданий час Густина розподілу часу відновлення Середній час відновлення Інтенсивність відновлення
Довговічність		Гамма-відсотковий ресурс Гамма-відсотковий термін служби Середній ресурс Середній термін служби
Збережуваність		Гамма-відсотковий термін збереження Середній термін збереження
Комплексна властивість надійності		Коефіцієнт готовності Коефіцієнт технічного використання Коефіцієнт оперативної готовності Коефіцієнт збереження ефективності

У наступних розділах викладаються інженерні методи розрахунку показників надійності на стадіях дослідження, обґрунтування й розробки об'єктів (розділ 3), методи статистичної оцінки цих показників у процесі випробувань й експлуатації (розділ 4), а також шляхи й методи забезпечення необхідного рівня експлуатаційної надійності (розділ 5), де основна увага приділена питанням структурного резервування як ефективного методу забезпечення нормального функціонування об'єктів, методи та засоби технічного діагностування (розділ 6).

5. Показники безвідмовності об’єктів, які не відновлюються.

5.1. Імовірність безвідмовної роботи. Імовірність відмови

Відповідно до ДСТУ 2860-94, імовірність безвідмовної роботи p(t) - це ймовірність того, що протягом заданого наробітку t відмова об'єкта не виникне. Наробіток об'єкта позначимо буквою Т і запишемо:

Цей запис читається так: імовірність того, що випадковий наробіток T не менше деякого заданого значення наробітку t.

Імовірність протилежної події є ймовірність відмови об'єкта. Імовірність відмови q(t) – це ймовірність того, що об'єкт відмовить у межах заданого наробітку t, тобто

Очевидно, що .

Неважко зрозуміти, що – це інтегральна функція розподілу випадкової величини .

Характерний вигляд функції і показаний на рис. 2.1.

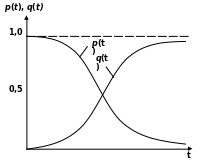
Рис. 2.1

Вище наведені так звані імовірнісні визначення показників і .Тепер розглянемо їхні статистичні визначення. На практиці значення цих показників можуть бути знайдені за статистичним даними про відмови об'єкта, отриманими в результаті випробувань об'єкта на безвідмовність. У цьому випадку визначаються наближені значення показників, називаються їхні статистичні оцінки. Для отримання формул статистичних оцінок скористаємося наступним прикладом. Нехай у момент часу поставлені на випробування справних об'єктів. У процесі випробувань через рівні проміжки часу перевіряється стан усіх об'єктів і визначається число справних об'єктів , де . об'єкти, Число об’єктів, які відмовили, не змінюється. Процес випробувань зображений на рис. 2.2 у вигляді тимчасової діаграми.

Визначивши в ході випробування всі значення , можна побудувати графік (східчасту функцію) для відносного числа справних об'єктів . Цей графік (див. рис. 2.2) є статистичною оцінкою ймовірності :

(2.1) ¹

Рис. 2.2.

Якщо процес виникнення відмов однорідний, то зі збільшенням і при одночасному зменшенні ступінчастий графік наближається до плавної кривої .

Аналогічним чином можна було б побудувати графік статистичної оцінки ймовірності відмови й одержати

. (2.2)