§ 4. Показательные, логарифмические, обратные и тригонометрические функции

Если функция y зависит от аргумента x, находящегося в показателе степени какого либо числа a, то такая функция называется показательной и записывается следующим образом: y =с a^kx . (8)

С показательными функциями часто приходится иметь дело, рассматривая процессы эволюции, накопления, роста, распада и т.п., с чем мы встретимся несколько позже. Особенно важны при описании этих процессов частные случаи показательной функции, когда в качестве величины a берется иррациональное число е ≈ 2,718282… (основание натуральных логарифмов). Функция вида y = е^kx называется экспоненциальной и в одну строку обозначается y = еxp[kx]. График этой функции называют экспонентой. Построим график показательной функции y = 2^x с помощью таблиц ее значений:

y

x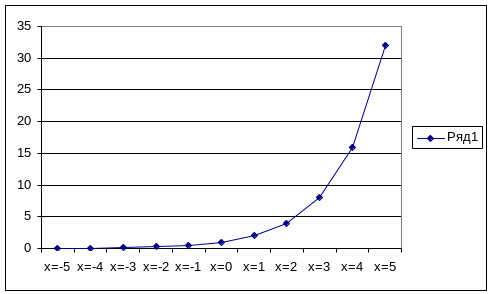

Рис.9. График показательной функции y = 2^x

Показательная функция приводит к логарифмической функции, если форма зависимости переменных меняется. Возникает вопрос, как зависит аргумент x от функции y, если y(x) является показательной функцией от x?

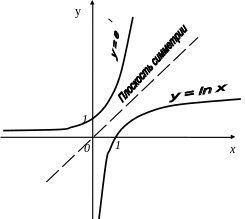
Для ответа на этот вопрос воспользуемся определением логарифма: логарифмом числа y по основанию a называется показатель степени x, в который надо возвести основание a, чтобы получить данное число y. Коротко определение логарифма записывается так: x = log_a y. Если попрежнему выражать функциональную зависимость как y(x), то определение логарифма следует переписать в виде: y(x) = log_a x . Такая форма записи означает , что существует показательноя функция, у которой основанием является число a, а показателем степени величина y. Поэтому функция показательная должна быть записана следующим образом: x = a^y. Сравнивая полученное выражение с записью показательной функции (8) при с = 1, k=1 замечаем, что произошла замена переменных x ↔ y. На графике, приведенном на рис. 9, таким образом, логарифмическая зависимость будет совпадать с показательной функцией, у которой произведена замена переменных. Результат построения на одном графике показательной и логарифмической функций изображен на рис. 10. В качестве основания на графике выбрано число е, а поэтому изображены экспоненциальная и соответствующая ей функция натурального логарифма.

Рис.10. Связь показательной (e^x) и логарифмической (lnx) функций

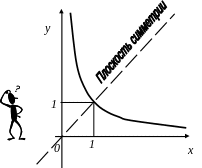
Степенная функция приводит к обратной функции, если показатель степени является отрицательной величиной. По правилам возведения в степень, отрицательный показатель означает, что переменная в степени попадает в знаменатель. Поэтому запись y =ax^-n можно представить в виде дроби: y =a/ xⁿ. Произведение степенной функции на соответствующую обратную функцию даст постоянную величину. Так например, в социально-экономических расчетах уже давно замечено, что при перераспределении денежных средств в государстве (по принципу социальной справедливости) процентная доля людей с большими доходами уменьшается, а доля людей с малыми – возрастает. При этом, произведение доходов R на соответствующий этим средствам процент населения (N) остается, как правило, постоянным (правило Парето): R·N = const. Обозначив константу единицей, получим , что функции R и N обратны друг к другу: R =1/N, а N = 1/ R. График обратной функции y = 1/x (при y>0, x>0) приведен на рис.11, а соответствующая кривая называется гиперболой.

(?): Какие из известных Вам процессов также изображаются на графике в виде гиперболы?

Рис. 11. График функции y = 1/x

Последний вид функций, которые имеют очень широкое распространение в реальной жизни, служит для описания периодических процессов. Они базируются на тригонометрических величинах синуса, косинуса, тангенса и котангенса, которые, в свою очередь, определяются с помощью равномерного движения точки по окружности. В социальной среде периодические процессы часто связаны с сезонными изменениями условий жизни, производства, климата и т. п. Согласование периодических процессов, происходящих с различной частотой или различными периодами является одной из наиболее сложных задач управления этими процессами в реальной жизни, поиском устойчивого развития производства, экономики, общества.

Выберем в качестве примера одну из периодических функций

y = sin x, график которой с периодом Т = 2π представлен на рис. 12. Областью определения функции является x (-∞, ∞), а область значений функции y [-1, 1].

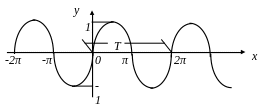
Рис.12. График функции y = sin x