§ 3. Квадратичные и степенные функции.
Доход, получаемый от продажи на рынке количества товара Q по цене P за единицу товара легко вычислить, умножая количество товара на его
цену: R = PQ+ R0, где R0 может означать величину дохода, полученного на предыдущем этапе. В то же время, сама цена P при различном спросе и
предложении может являться функцией количества товара P(Q). Если эта функция является линейной, то есть P(Q)=aQ +b, то величина дохода в зависимости от количества товара, реализованного на рынке, запишется так:
R = PQ+ R0 =aQ2+bQ+R0. Абстрактно, полученный вид зависимости можно представить следующим образом: y = ax2 + bx + c. (6)
Функция y(x) называется квадратичной по наибольшей степени аргумента x, равной двум. Если наибольшую степень аргумента в общем виде обозначить n (n ≥ 2), то функции от таких аргументов называют степенными. При дробном показателе степени (n=1/2, 1/3, …) извлекается корень из переменной x, величина которого приводит к иррациональности для некоторых точек, то есть к невозможности записать соответствующее значение функции конечным числом цифр на всей области определения функции. Такие иррациональные функции называют степенными функциями с дробными показателями степени.
Исследуем квадратичную функцию, как наиболее простую среди степенных функций. Построение конкретных графиков функций произведем по точкам, используя программу Excel.
Пример 1. y = 2x2. (рис.7)
y
0 2 8 18 32 50 …..
± x
0 1 2 3 4 5 ……
|
y
x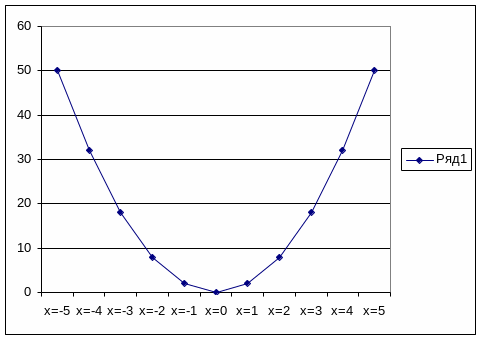
Рис. 7. График квадратичной зависимости при а = 2, b = 0, c = 0
Пример 2. y = 2x2 +4x – 1 (рис.8)
y
x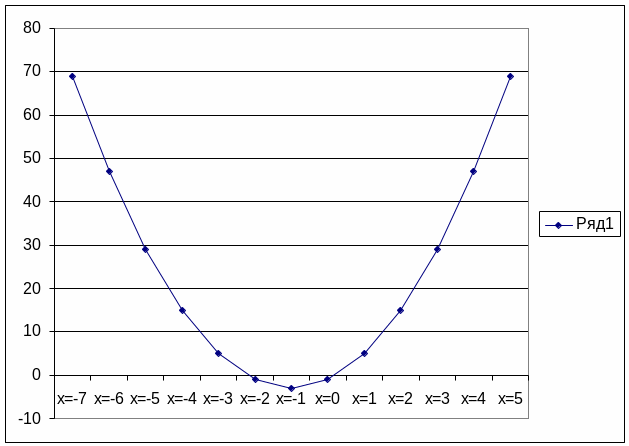
Рис.8.
График квадратичной зависимости при
a=2,
b=4,
c
= -1
Для вычисления точек пересечения графика функции с осью 0x необходимо решить квадратное уравнение 2x2 + 4x – 1 = 0 , так как только на этой оси значение функции y = 0. Тогда, по правилам поиска корней квадратного уравнения (см. справочник по математике), получим:
.
Из свойства симметричности графика (рис.8) следует, что минимальное значение функция принимает при x = (x2 + x1 )/2 = – 1, что хорошо подтверждается на графике. Кривая линия, графически представляющая квадратичную функцию, называется параболой.
Для построения по точкам графика сложной (n ≥ 5) степенной функции
y = a0x0+a1x1+a2x2+…+anxn (7)
при заданных коэффициентах ai можно, как и выше, воспользоваться составлением обычной таблицы значений аргумента и функции.
При больших n полезно составить простую программу суммирования отдельных слагаемых в правой части функции, которая представляет собой многочлен n – й степени. Основная сложность представления функции заключается в том, что ее вид зависит от выбранного интервала значений аргумента. При x → ∞ функция приближается к параболе n – й степени: y = anxn . Это происходит в том случае, когда коэффициенты ai меняются медленно. Поэтому при больших значениях аргумента xn >> xn-1 (символ >> означает «намного больше») и остальными слагаемыми многочлена можно пренебречь.