Тема 5. Индексный метод в исследовании социально-экономических явлений. Социальная статистика.

Статистические индексы используются для сопоставления показателей в экономике, при мониторинге деловой либо любой другой активности, при определении уровня жизни и в этом смысле, рассматриваемая тема является в основном социальной. Индекс является относительной величиной, полученной при сопоставлении тех или иных социально-экономических показателей во времени, в группе организаций или систем, а также при прогнозировании и планировании.

В экономике, где индексный метод получил наибольшее распространение, чаще других используют индексы цен (i_p) и индексы физических объемов продукции (i_q):

и , где величины и характеризуют,

соответственно, цены и количество i-го вида товара, включая акции и другие ценные бумаги, за отчетный j-й период, а 0-й период выбран в качестве базисного. Эти индексы называются индивидуальными. Использование индивидуальных индексов не всегда удобно, так как на предприятии могут выпускать различные виды товаров, несоизмеримые по цене и по количеству (кнопки и автомобили, например). Единой меркой для них может служить произведение цены товара на его количество. В этом случае мы приходим к так называемым агрегатным индексам цен и физических объемов:

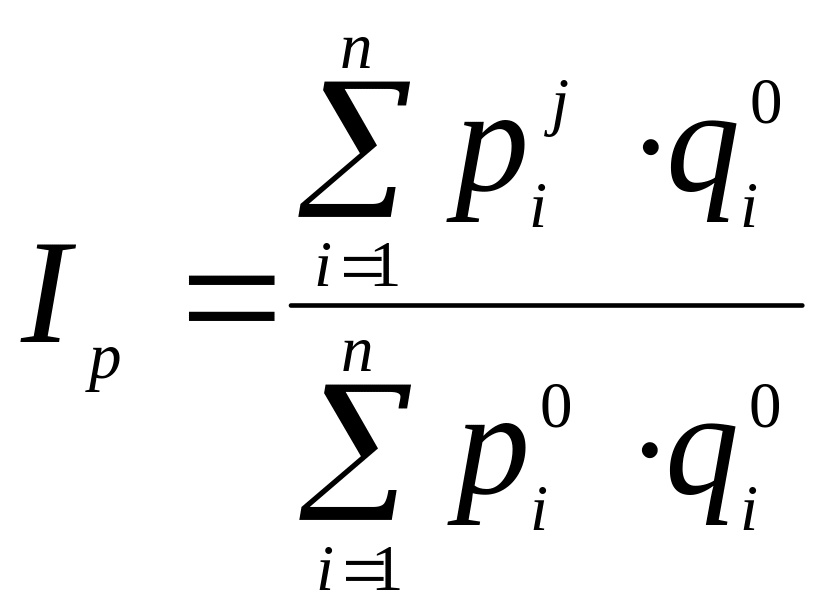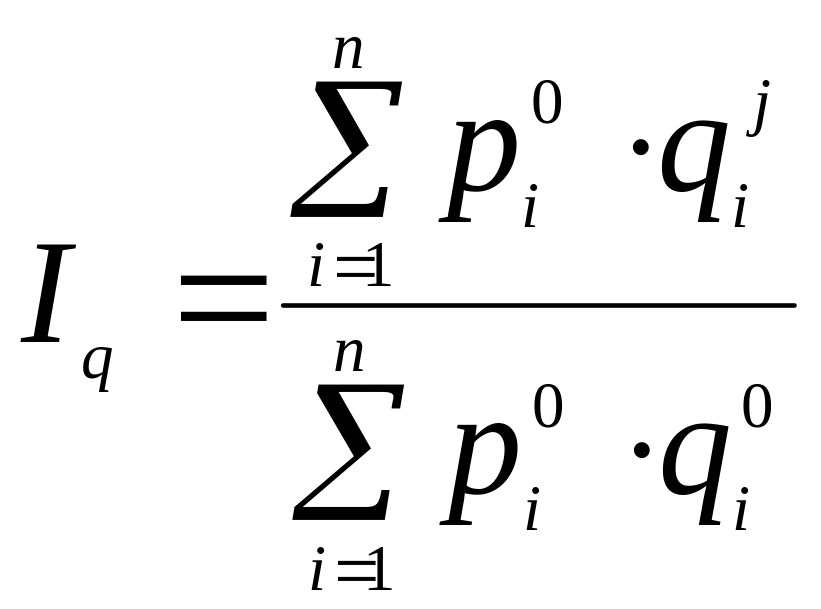; (формулы Ласпейреса).

Расчеты основываются на ценах и количестве товаров некоторого периода, взятого за базисный. Возможны и другие подходы.

С помощью индексов фиксируется состояние рынка ценных бумаг(акции, облигации, опционы и др.). Можно выделить интегральные и частные индексы. Так, например, сводный индекс Доу-Джонса рассчитывается по акциям 30 крупнейших промышленных корпораций, 20 транспортных и 15 коммунальных и является интегральным, но он может быть дополнен расчетом частных индексов по отдельным промышленным компаниям.

Важную роль при выборе экономических решений в государстве играет величина индекса потребительских цен, называемый иногда индексом стоимости жизни. Формула его расчета приводится ниже:

,

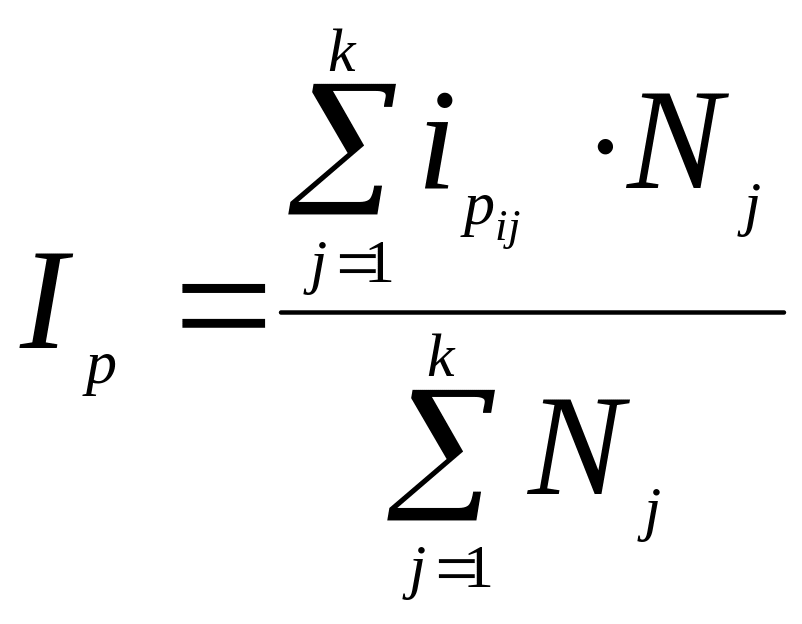где i_pij- индивидуальный индекс цен i-го товара на j-й территории;

- численность населения j-й территории;

k – число территориальных единиц.

С 1992 года потребительская корзина в России, используемая для расчета индекса потребительских цен, охватывает 409 групп товаров, в том числе 103 позиции продовольственных, 222 – непродовольственных товаров и 84 позиции платных услуг. Так, например, в 1994 году наблюдение проводилось в 834 городах Российской Федерации. Таблица 9.10 (Приложение) приводит данные индексов цен за июнь 1994 года, отнесенных к декабрю 1993 года, откуда видно, что это отношение, усредненное по всем потребительским товарам составляет величину 1,75, а следовательно, цены за этот период возросли на 75%. Таким образом фиксируется уровень инфляции.

П Р И Л О Ж Е Н И Е II

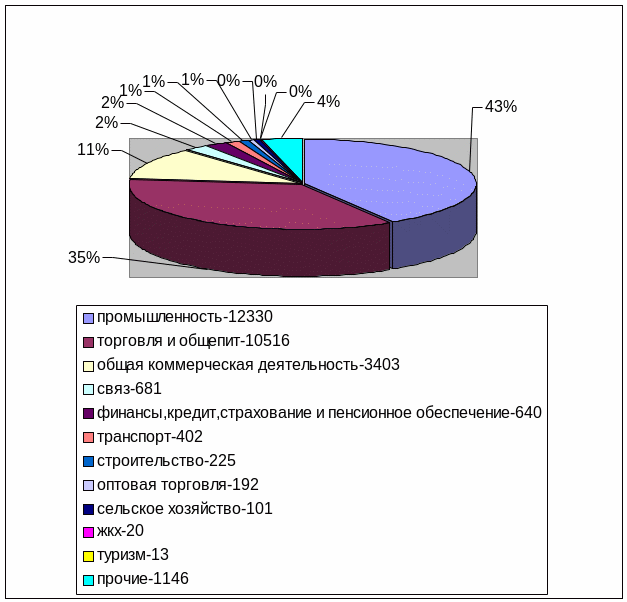
Отраслевая структура иностранных инвестиций в Российскую Федерацию в 2003 году (млн. долларов)

товарооборот( € )

Линия тренда

Скользящая средняя

Уровни динамики

кварталы года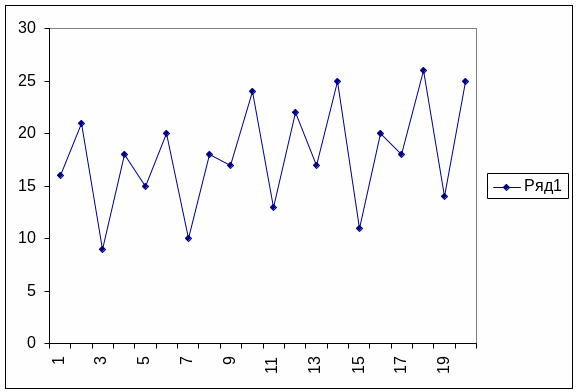

Рис. Динамика товарооборота магазина за 5 лет

Фактические уровни ряда динамики(1)

5-дневная скользящая средняя (3)

3-дневная скользящая средняя (2)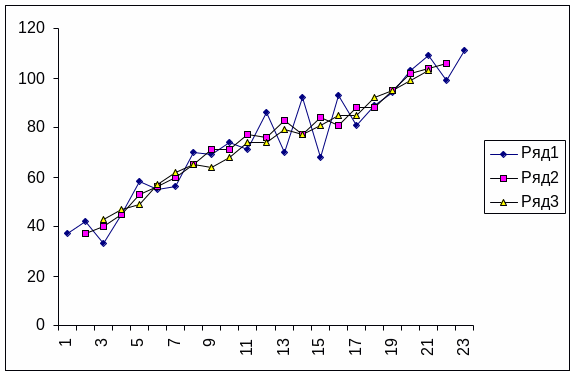

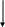
Рис. Сглаженный ряд динамики объема выпуска продукции по месяцам

П Р И Л О Ж Е Н И Я III

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

1. Математическая модель размножения бактерий.

Запишем уравнение, которое было получено при анализе процесса размножения клеток в питательной среде: (III.1) , для решения которого воспользуемся методом разделения переменных:

, откуда поиск функции u(t) производится интегрированием: . Решение для левой части уравнения можно записать, используя математические таблицы неопределенных интегралов. Сравнивая табличное выражение (13) в Приложении I с последним уравнением, замечаем, что при a = – g ; b = k; c = 0; u = x они совпадают и Δ = 4ac – b² = – b² = – k², то есть Δ < 0. Поэтому интегрирование левой и правой части приводит к равенству:

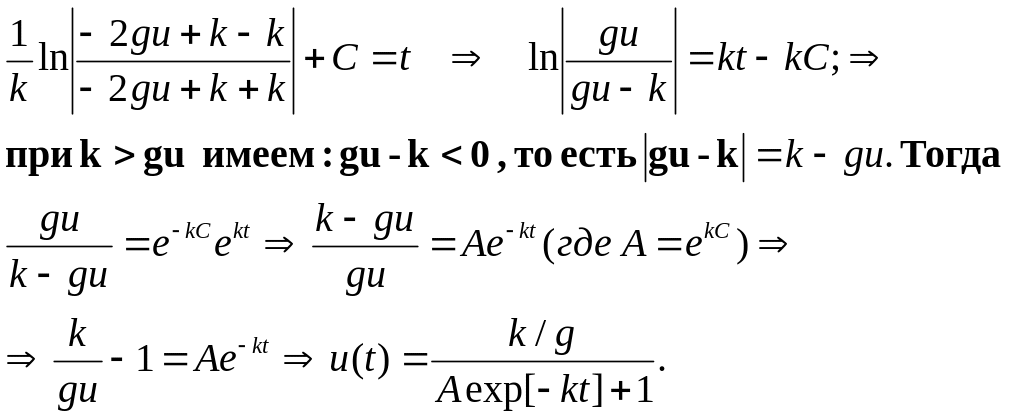
Условие k > gu является оправданным потому, что в начальный момент времени (t = 0, u = u₀ = 1(одна клетка)) скорость роста должна быть положительной величиной. Иначе процесса роста наблюдаться не будет.

Проведем анализ полученного решения : .

При t→ 0, exp[-kt] → 1, а u(t) → const = u_0. С течением времени знаменатель дроби в решении u(t) засчет экспоненциальной функции уменьшается и количество клеток растет. Если на начальной стадии величина Aexp[-kt] >>1, то рост клеток «идет» почти по экспоненциальному закону, а затем, при t → ∞ величина Aexp[-kt] становится близкой к нулю и количество клеток «выходит» на стационарную фазу роста: u(t) → k/g.

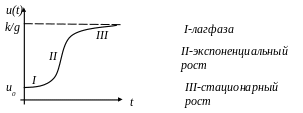
Рис. 6. Диаграмма роста

На рис.6 изображена диаграмма роста бактерий в питательной среде, соответствующая особенностям функции u(t). Большая часть ростовых процессов, рассматриваемая в экспериментальной биологии и демографии, имеет аналогичный вид и на диаграмме анализируемого процесса обычно выделяются: фаза накопительная (I), называемая лаг – фазой, (II) – фаза размножения (экспоненциального роста) и (III) – стационарная фаза. Переход от фазы экспоненциального роста к стационарной фазе обычно ассоциируют с моментом возникновения «экологических» проблем, связанных с накоплением в среде продуктов отхода от деятельности организмов. Исследование уравнения роста при произвольных значениях коэффициентов k и g математическими методами приводит к дискретному аналогу дифференциального уравнения III.1. Если состояние системы фиксируется не непрерывно, а в определенный момент времени (t = 1, 2 и т.д.), то уравнение для каждой переменной u(t) переходит в уравнение с переменной u_t, которое относительно легко решается численными методами. Так, например, рост популяции какого-либо биологического вида с численностью u(t), фиксируемой по годам (t равно 1 году), может быть описан так называемым логистическим уравнением: u_t+1 = cu_t (1 – u_t), в котором первое слагаемое cu_t характеризует рост популяции, а второе –cu_t² (нелинейный член) – определяет ее убыль (см. §8, ЧастьI). Как показал анализ решения, многое зависит от параметра c: однозначность или неоднозначность поведения системы при различных условиях при наличии небольших флуктуаций параметров.

При c < 1 популяция вымирает, при 1 < c < 3 численность растет, при 3 < c < 3,4 наблюдается две ветви (бифуркация), между которыми происходят колебания численности, при 3,4 < c < 3,54 имеется 4 ветви и т.д. и численность начинает "скакать" между ними. При c > 3,57 движение приобретает хаотичный характер (детерминированный хаос). Состояния "перемешиваются" (рис. 7).

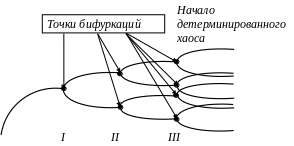
Рис. 7. Этапы развития системы

В более сложных системах на каждом переходном этапе точки бифуркаций становятся точками ветвлений и диаграмма процесса принимает вид дерева графа – особой математической структуры, характеризующей множество точек с заданным отношением связи между ними, называемыми ребрами графа. Рис. 7 является частным случаем такой математической структуры. Примерами графов являются алгоритмы разветвленных программ, нейронные сети, транспортные сети, денежные потоки в экономике и многое другое. Последние годы особый интерес почти во всех науках, где используются математические модели эволюционных процессов или процессов роста, привлекают так называемые «растущие» ориентированные (направленные) графы. Применение такого моделирования рассмотрим ниже в последнем примере 4 Приложения III.

2. Модифицированная модель Лотки – Вольтерра и проблема

обучаемости

Механизмы принятия административных решений в системе образования могут быть эффективными, если им предшествуют предварительные расчеты, основанные на математических моделях. Особенно остро в последнее время стоит вопрос о выявлении конкретной способности индивидуумов к обучению («обучаемости»), количественной мерой которой может служить время, необходимое для прочного усвоения определенного объема информации. Без решения задачи обучаемости в зависимости от времени невозможно принятие научно обоснованных решений по распределению часов, отведенных на тот или иной предмет (блок предметов) в образовательных стандартах, по объему нагрузки на школьников и студентов, и т. п. Именно поэтому возрастает значимость тестирования, позволяющего делать по результатам обучения определенные «срезы знаний» во времени.

Тем не менее, важность исследования обучаемости в зависимости от времени в явной форме, в виде определенной функции ε (t) также несомненна. Здесь требуются глубокие психолого-педагогические подходы, информация о которых на сегодняшний день слишком мала.

В рамках данного учебника можно лишь продемонстрировать фундаментальность функции обучаемости, являющейся необходимым элементом деятельности не только в человеческом обществе. Особенно велика роль обучения в условиях соревнований, конкурентной борьбы, борьбы «за выживание», борьбы «на уничтожение» и т. п.

Ниже рассмотрим две такие системы с элементами обучаемости, которые базируются на расширении известной в синергетике и биологии модели Лотки – Вольтерра (модели «хищник - жертва»):

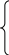
= α₁N – β₁NM, (1)

= – α ₂ M + β₂ NM,

где N – количество «кроликов – жертв» в системе с неограниченным резервом травяной пищи для них, а M – количество «рысей - хищников», рост которых зависит от вероятности встреч хищника с жертвой. Эта вероятность пропорциональна произведению NM. Одновременно, от вероятности такой встречи уменьшается число кроликов. Поэтому в верхнем уравнении системы (1) слагаемое в правой части, пропорциональное произведению NM, стоит со знаком минус. Коэффициенты α₁, α₂, β₁ и β₂ в этой системе являются константами, а их смысл обсуждается в любом издании (область биологии и синергетики).

Новая постановка задачи выживаемости (конкурентоспособности), которую предлагается проанализировать, заключается в том, чтобы ввести в систему уравнений (1) зависимость коэффициентов β₁ и β₂ от времени и считать их связанными с функцией обучаемости ε (t) в виде β₁(t) = β₂(t) = , где ε_N (t) – обучаемость кроликов, а ε_M (t) – соответственно, обучаемость хищников во времени.

Очевидно, что чем быстрее растет обучаемость кроликов по сравнению с обучаемостью хищников, тем меньше величина β₁ (t) и β₂ (t), что в свою очередь приводит к благоприятным условиям «выживания» кроликов. Если приблизиться к реальности, то ε_N (t) и ε_M (t) могут быть периодическими функциями с разными частотами, могут зависеть от N и M, что будет означать распределение кроликов и рысей по их способностям к обучению и т. п. В этих случаях, результаты расчетов для зависимости N(t) и M(t) заранее не предсказуемы даже качественно и решения будут зависеть от всех констант и параметров распределений.

Имеют право на существование и другие направления исследований в рамках модифицированной модели Лотки – Вольтерра с элементами обучаемости. Если говорить о борьбе за выживание среди людей, то в первую очередь, следует иметь в виду боевые действия. Так как время, деньги, ресурсы и информация являются всеобщими эквивалентами обмена, то и переменная t в системе уравнений не обязательно играет роль времени. Так, например, во время театра военных действий, величины и N(t) могут иметь смысл скорости изменения (и численности) военнослужащих в зависимости от денежных затрат, выделенных ресурсов, снабжения информацией и т.п.

Очевидно, что множества военнослужащих N и M являются одновременно и хищниками и жертвами, а систему уравнений может представить следующим образом:

= α ₁ (N_p – N) – β₁NM, (2)

= α ₂ (M_p – M) - β₂ NM.

где N_р и M_р – константы, определяющие резервное количество военнослужащих, а β₁ и β₂ по прежнему могут быть связаны с функциями ε₁(t) и ε₂ (t), но уже не только от времени (хотя и это остается в силе), но и от денежных затрат, ресурсов и информации. Похожие уравнения можно ввести и в экономике, анализируя выживаемость фирм на рынке в условиях конкуренции. Но во всех рассматриваемых системах функция обучаемости (информированности, компетентности, профессионализма) является едва ли не основным фактором выживания.

Если, например, ε(t) = at + b, т. е. функция обучаемости имеет простейший вид линейной зависимости от времени, то коэффициенты а (выражающий среднюю способность индивидуумов к обучению) и b (определяющий стартовый уровень знаний, умений и навыков, и даже культуры) по величине, в общем случае, различны, что сказывается на конечном результате. Необходимо проведение практических исследований, прежде чем они могут быть использованы для решения задач в конкретной ситуации. По-видимому, а и b могут быть ранжированными параметрами, для которых необходимо вводить некоторый набор эталонов, как это делается, например, в психологии.

Тем не менее, сама система уравнений (модель) имеет прогностическую ценность, так как она позволяет, «играя с параметрами», выявить устойчивые решения и условия, при которых осуществляются различные «сценарии». В этом случае сценарии, определяемые уравнениями (1) и (2), могут служить основой для построения определенной деловой игры, в которой выигрышем является угадывание результатов решения, т.е. правильное прогнозирование поведения системы, развитие интуиции.

Приведем лишь два конкретных примера (а их много и обсуждать их следует отдельно) по результатам исследования модифицированной системы (1) при заданных параметрах функции обучаемости (рис.1а,б). Так как нелинейные уравнения не имеют общих аналитических способов их решения, то решение было получено на компьютере численными методами (программа «Mathcad»).

На рис.1а представлены изменения популяций хищников и кроликов в зависимости от времени (три первых диаграммы а,б,в и фазовая траектория (г) для величин N и M) при ε_N(t )= ct²+d и ε_M(t)= at+b, а на рис.1б при ε_N(t) = ct + d и ε_M(t) = at+b.

Анализируя результаты расчетов, легко заметить, что вместе с увеличением количества кроликов во времени растет и число хищников, а фазовая диаграмма (г) имеет вид разворачивающейся спирали. Если же проводить экспериментальные исследования, опираясь на информацию о числе хищников, то наблюдаемое увеличение их популяции могло бы навести на неверный вывод о том что, как следствие, количество кроликов должно уменьшаться, а оно также увеличивается (?!).

(а)

(б)

(г)

(в)

Рис. 1а. Результат решения уравнений (1) при нелинейной

зависимости ε_N(t) от времени.

Рис. 1б. Результат решения уравнений (1) при линейной

зависимости ε_N(t) и ε_M(t) от времени (а > c)

В модельном эксперименте, представленном на рис. 1б, хищники обучаются немного быстрее, чем кролики и это приводит к постепенному уменьшению как жертв, так и их врагов. Интересным фактом является наличие периодичности во времени, похожей на «резонансные» движения качелей в первом случае (рис. 1а) и на затухающие колебания – во втором (рис. 1б). Очевидно, существует стационарный процесс саморегуляции количества хищников и кроликов, при котором совершаются колебания численности и тех и других во времени с постоянной амплитудой. Этот эксперимент уже поставлен природой. В Канаде была накоплена информация о количестве кроликов и рысей в лесу за несколько лет, которая позволила сделать вывод о стационарности процесса: колебания числа кроликов опережают колебания для количества рысей, о чем можно прочесть в учебной литературе по синергетике. Параметры β₁ и β₂ при стационарном состоянии биологической системы в модели (1) не зависят от времени, то есть являются постоянными. Математическое моделирование привело к адекватному описанию фактов.

При отсутствии у кроликов врагов (M = 0), решение верхнего уравнения в системе (1) приводит к экспоненциальной функции роста количества кроликов, что легко проверить самостоятельно. Известен факт резкого увеличения популяции кроликов в Австралии, где для них не нашлось естественных врагов.

Тем не менее, закон экспоненциального роста указывает лишь тенденцию хода процесса, в то время как более детальное изучение закономерности роста кроликов (без врагов) показало, что этот рост следует по порядку числам в ряду последовательности Фибоначчи: 1,1,2,3,5,8,13,21,… , который строится по правилу: F(n+1) = F(n) + F(n –1), где F(n) – число, стоящее в ряду последовательности на n-м месте. Этот экспериментальный факт показывает, что размножение кроликов происходит медленнее, чем при экспоненциальном росте.

3. Исследование модели случайного процесса, подчиняющегося устойчивому распределению Коши.

Рассмотрим соотношение между динамическими и статистическими моделями на примере одного из наиболее распространенных симметричных распределений случайной величины, называемого распределением Коши.

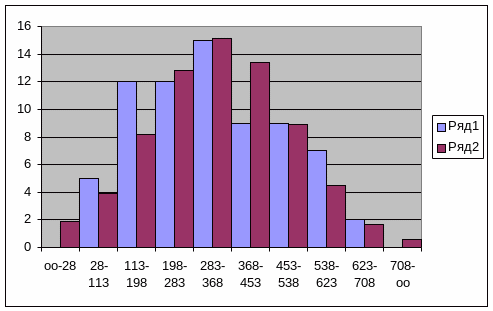
Пусть при проведении эксперимента, относительная частота встречаемости, приходящаяся на единичный интервал некоторой случайной величины x (цены товара на рынке), привела к гистограмме процесса, изображенной на рис.2.

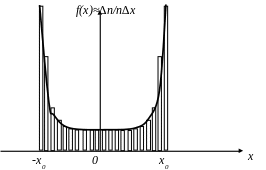
Рис. 2. Гистограмма рыночных цен на отдельные товары

При проведении эксперимента были замечены две особенности. Первая заключалась в том, что при наблюдении процесса в случайные малые интервалы времени dt случайная величина, естественно, фиксировалась хаотически, но за некоторое определенное время наблюдения Т₀ заполнила почти все значения в интервале от –x₀ до+x₀ . Вторую особенность легко заметить на гистограмме. Она заключалась в том, что при любом реальном увеличении интервала времени наблюдения, значения случайной величины не выходили за пределы указанного интервала.

Выбор аппроксимирующей функции плотности вероятности, на деталях которого останавливаться не будем, приводит к известному в статистике распределению Коши: .

График этой функции изображен на гистограмме непрерывной жирной линией. Очевидно, что распределение Коши отражает все особенности проведенного эксперимента. Не анализируя причин изменения цены товара с течением времени, выясним динамику цены, которая можен быть представлена видом функции x(t) (цена в зависимости от времени).

Вероятность наблюдения цены x за фиксируемый малый интервал времени dt при условии, что существует полный интервал наблюдения T₀, может быть записана по определению вероятности как dp(x) = dt/T₀. С другой стороны, исходя из определения функции плотности вероятности, имеем: dp(x) = f(x)dx. Поэтому справедливо следующее равенство:

.

Так как переменные в этом уравнении уже разделены, то легко получить результат x(t) интегрированием левой и правой части. Правая часть содержит функцию, интеграл от которой дан в Приложении I (№7). Тогда имеем:

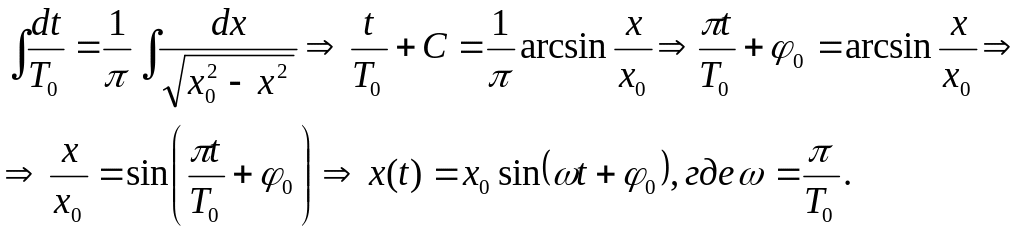
Очевидно, что рассматриваемая модель процесса изменения цены на товар, функция плотности вероятности которой подчиняется распределению Коши, является динамической моделью периодического процесса. Если основными параметрами системы рынка считать цену товара и скорость ее изменения, то в фазовом пространстве состояний системы для каждого момента времени можно ввести вектор состояния . Так как связь переменных со временем выражается через тригонометрические функции, то можно записать: , откуда следует, что и тогда

На диаграмме состояний, построенной в переменных x и x’, полученное уравнение будет представлять собой эллипс (рис.3). Эта кривая второго порядка в данном случае называется фазовой траекторией и представляет собой еще одну модель рассматриваемого процесса. Так как основные переменные на фазовой траектории согласованы во времени, то процесс называется стационарным. Не изменяющимися характеристиками процесса являются полуоси эллипса, то есть величины x₀ и x₀ω, а также величина площади эллипса S = πab =π ωx₀².

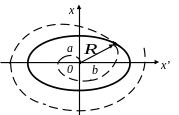
Рис. 3. Фазовая траектория процесса изменения цены

Сам факт наличия периодичности в поведении цены товара на рынке не раскрывает причину возникновения этой периодичности, поэтому использование модели для целей прогнозирования ограничены. Качественно, возникающие колебания можно объяснить коньюнктурой рынка, соотношением между спросом и предложением, «преследующими» противоположные цели (принцип единства и борьбы противоположностей в диалектике). Одну из подобных моделей мы рассмотрели выше, анализируя ситуацию в системе «хищник – жертва», в рамках которой колебания возникали естественным образом, а фазовые диаграммы имели вид овала в стационарном состоянии или вид спирали (расходящейся или свертывающейся) в фазовом пространстве состояний при нестационарном процессе (рис.1а(г), 1б(г)). В принципе, в рассматриваемой модели, на колебания цены (путем администрирования) можно накладывать ограничения как на величину максимальной цены, так и на скорость ее изменения и тем самым добиться либо «затухающих» колебаний, либо «резонансных» (рис. 3 – пунктирные фазовые траектории). Но прежде чем принимать подобные административные решения, следует более глубоко разобраться в самих причинах этих колебаний. Так например, в системе «хищник – жертва», в которой наблюдаются периодические изменения численности популяций как результат самоорганизации, непродуманное вмешательство человека («администратора») может нарушить хрупкий баланс стационарного процесса и привести к непредсказуемым последствиям.

Приведенный выше анализ систем, поведение которых основано на процессах самосогласования параметров, с необходимостью приводят к выводу о том, что всякому принятию конструктивного решения должна предшествовать работа по построению прогностической модели эволюции (роста, накопления, развития и т.п.) этой самоорганизующейся системы. Ниже рассмотрим одну из таких моделей.

4. Дискретная модель накопления и роста.

Пусть мы имеем фазовое пространство состояний эволюционирующей системы, для которой определены основные социально-экономические параметры (ВРП, Накопления, Ресурсы и т.п.), выраженные в определенных единицах измерения. Пусть также в этом пространстве могут существовать элементарные производители, объединяющиеся между собой внутренними и внешними связями. Под словом «существовать» будем понимать «иметь определенные параметры». Наличие внутренней связи между элементарными производителями будет указывать на их объединение в одну подсистему, а наличие внешних связей будет характеризовать взаимодействие подсистем между собой.

Для элементарной подсистемы количество внешних связей ограничено и возникает стремление к расширению, то есть к увеличению числа связей, путем их объединения в подсистему. Процесс «накопления» параметров в фазовом пространстве будет означать переход всей системы с условно выбранного начального (нулевого) состояния на новый уровень с увеличенными параметрами. Если параметры меняются дискретно, то совокупность большого числа переходов (за относительно большой промежуток времени) приведет фазовое пространство, в котором зафиксированы все этапы эволюции, к разбиению на отдельные, в общем случае, не элементарные замкнутые области (вершины графа).

Общие границы между отдельными подсистемами в разбиении выделяют «соседей» выбранной подсистемы, другими словами, количество внешних связей (ребер графа). Таким образом, результат развития системы, будет геометрически представлять собой своеобразную «карту местности» (рис.9), на которую наложен «растущий» из начальной области граф.

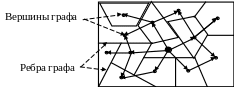
Рис. 9. Дерево эволюции системы

Тем не менее, развитие системы, происходящее без разрыва связей должно выглядеть как переход от первого «окружения» исходной области ко второму окружению и т.д. с соблюдением принципа сохранения локальных (индивидуальных) правил соседства. Исследование разбиений показало, что хаотически распределенные локальные связи между подсистемами не приводят к устойчивой динамике роста, пока в качестве согласования на связи не будет наложено условие симметрии. Учитывая важность периодических процессов в природе, выберем в качестве симметрического преобразования элементарные трансляции, образующие решетку. Для конечного числа подсистем это приводит к понятию фундаментальной области периодического разбиения, состоящего из ограниченного набора этих подсистем, трансляционно размноженных (перенесенных) в основных направлениях изменения параметров системы.

Далее, выберем для определенности, в целях удобства представления, в качестве элементарного состояния квадратную ячейку. Тогда подсистемы будут представлять собой объединения клеток с общими сторонами (из двух клеток – домино, из трех – тримино, из большого числа клеток - полимино). Пространство возможных состояний системы, как мы уже определили раньше, будет представлено разбиением плоскости на полимино (рис. 10).

Рис. 10. Разбиение фазового пространства системы на подсистемы (пентамино)

Процесс эволюции системы начинается с выбора исходной подсистемы, ее первого окружения ближайшими соседями, затем второго окружения и так далее, пока не начинает выявляться стационарная структура роста ( Рис.11).

(1)

(2)

(3)

(5)

(4)

(6)

Рис. 11. Поэтапное развитие системы (1 - 5). Стационарная структура (6)

На рис. 12 выделены два ожерелья в более сложной системе из 14 полимино – подсистем, которые показывают определенные стадии развития системы, демонстрирующие эффект самоподобия в процессе накопления параметров.

Рис. 12. Два самосогласованных этапа развития системы

Если внутри фундаментальной области взаимодействующих подсистем убирать связывающие полимино границы, то это равносильно объединению их в одну подсистему. В этом случае ход эволюционного развития системы меняется. Легко доказывается, что объединение всех подсистем в фундаментальной области в монопольную единую систему (в двумерной, плоской модели) приводит только к двум возможным вариантам развития: шести- и четырехугольнику. Это однозначно указывает на отсутствие разнообразия при росте монопольных систем. В таких жестких системах сложно что-либо изменить, даже в том случае, когда появляется такая необходимость.

Если далее сравнить гетероструктуры с монополистическими, то при ухудшении условий, таких как сырьевые ограничения, перебои с энергоресурсами и другими видами ресурсов, монопольная система нарушает стационарный процесс накопления значительно быстрее.

Рис. 13.Ресурсы для гетероструктуры уменьшились «сверху» до 30%

Рис. 14. Ресурсы для гетероструктуры уменьшились со всех сторон до 30%

Структура продолжает рост, хотя и не в стационарном режиме.

Рис. 15. Ресурсы уменьшились до 45% в монопольной системе

Рост нестационарный.

При уменьшении ресурсов до 40% в монопольной системе вообще нет роста (!).

93