Тема 4. Выборочный метод. Корреляционные связи.

Для проведения статистических наблюдений и построения соответствующих распределений вначале важно выделить полное множество объектов, обладающих данным признаком. Это множество называют генеральной совокупностью. Как правило, генеральная совокупность содержит огромное (теоретически бесконечное) число элементов, поэтому наблюдение не в состоянии охватить всю совокупность и становится возможным только выборочное наблюдение. Часть единиц генеральной совокупности, подлежащая непосредственному наблюдению, называют выборочной совокупностью или выборкой.

Математическая статистика занимается определением свойств генеральной совокупности по свойствам выборки.

Так, экспериментальные распределения, вследствие своей ограниченности по сравнению с теоретическими распределениями, могут служить примером выборки случайных величин, которая характеризуется определенным уровнем доверительности. Вообще говоря, любая экспериментальная выборка репрезентативна (представительна) лишь в той или иной степени. Согласно теореме Ляпунова, при достаточно большом числе независимых наблюдений в генеральной совокупности с конечной средней и ограниченной дисперсией, вероятность того, что расхождение между выборочной и генеральной средней, не превзойдет по модулю величину произведения tμ , равна интегралу Лапласа Ф(t), рассчитанному в пределах от – t до + t (при μ² = <σ²_выб>). Обозначая выборочную среднюю <х_выб>,а генеральную (теоретическую) среднюю х_ср, имеем:

р(|<х_выб>–х_ср| ≤ tμ)=Ф(t).

Численное значение интеграла Лапласа

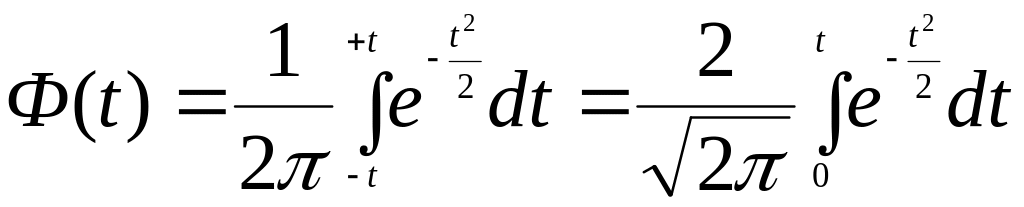
можно найти в справочниках по математике.

Доверительный интервал для генеральной средней заключен в пределах ±tμ. Величину t называют коэффициентом доверия. При t=1,96 доверительная вероятность равна 0,95 (95%), а при t=2,58 - 0,99 (99%).

Репрезентативность выборки из n величин генеральной совокупности была исследована Стьюдентом. Рассмотрим конкретный пример.

При проведении социально-экономических исследований по определению среднего уровня оплаты труда категории работников коммерческих банков было выяснено, что в выбранном регионе разница между наибольшим и наименьшим уровнем оплаты операционистов оказалась равной 3 тыс. руб. Если считать, что эта величина соответствует разбросу 6σ (от –3σ до +3σ), то оценка величины стандартного отклонения, судя по выборке, составляет 3000 руб./ 6 =500 руб. Для дальнейших расчетов, зададимся предельной ошибкой выборки в 100 руб. Обозначим эту величину Δ. С другой стороны, Δ не превосходит величины доверительного интервала tμ, где μ²=σ²_ср; σ²_ср = σ² /n, а n – размер выборки (количество обследованных операционалистов). Тогда можно записать:

Δ = tμ = . Откуда получаем, что . После подстановки данных, имеем: . Итак, необходима выборка из 100 человек. Подстановка величины t = 2 означает, что результат получен с уверенностью 95,4%.

Согласие между теорией и экспериментом можно оценить количественно, если отнестись к экспериментальным данным и теоретическим переменным в распределении как к системе, содержащей наборы из двух независимых величин. Критерий согласия между ними был предложен Пирсоном (χ² - критерий) и рассчитывается по отклонению экспериментальных частот от вероятностей теоретического распределения для одинаковых интервалов СВ.

Для проведения расчетов необходимо:

• произвести с экспериментальными данными процедуру центрирования и нормирования, т.е. перейти к новым переменным 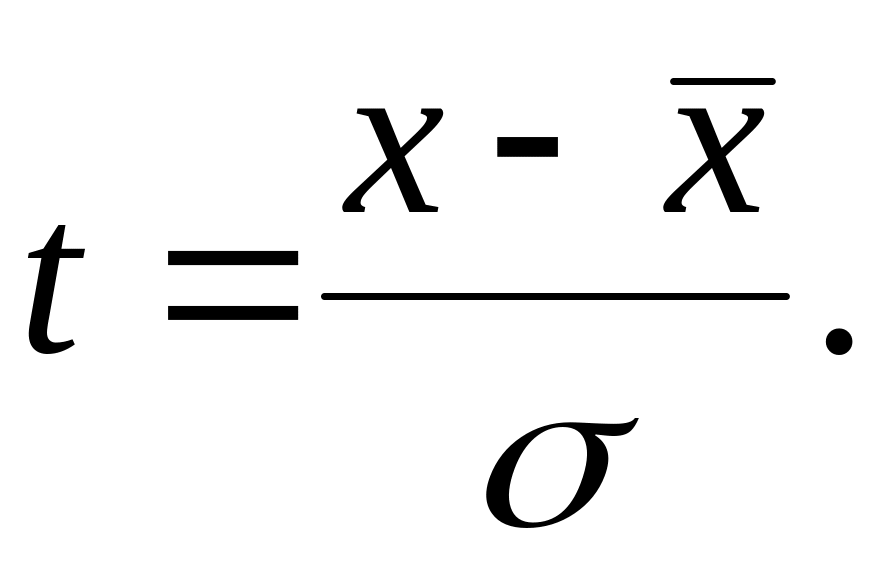Для каждого интервала затем необходимо вычислить t_Н(х_Н) и t_В(х_В). Эти значения будут опорными для перехода к теоретическому распределению;

• найти по таблицам величины интегралов 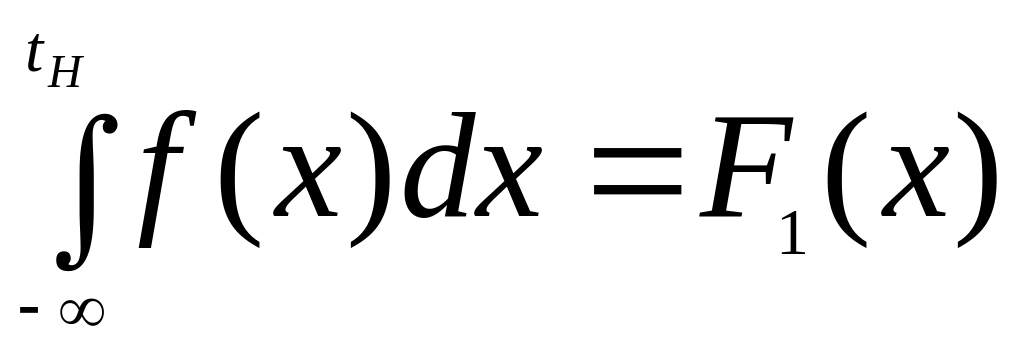и , что геометрически представляет собой площади под теоретической кривой распределения f(x) в пределах от – ∞ до правых границ, соответственно, t_Н и t_В ;

• рассчитать для каждого i-го интервала вероятность Р_i = F₁(x) – F₂(x) попадания СВ между t_iВ и t_iН ;

• рассчитать абсолютную частоту (m_i или f_i) появления СВ в каждом интервале умножением соответствующей вероятности Р_i на общее количество n – значений случайной величины. Действительно, по частотному определению вероятности Р_i = m_i/n = f_i/n ;

• вычислить критерий Пирсона по формуле:

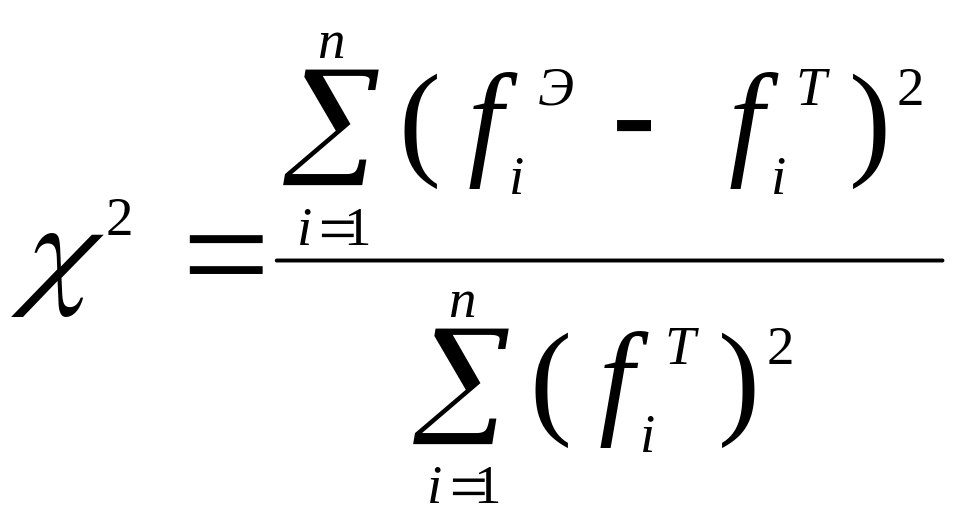, где верхние индексы частот относятся либо к экспериментальному (Э), либо к теоретическому (Т) распределениям.

Этапы подготовки экспериментальных данных для расчета критерия согласия представлены на конкретном примере в табл. 5.9, 5.11 (Приложение II ). Нумерация таблиц и другая информация в Приложении II взята в соответствии с первоисточником из учебника по Общей теории статистики [1]. В математических справочниках имеются таблицы значений критерия согласия, вычисленные в зависимости от числа степеней свободы (эта характеристика определяется как количество интервалов k –3) и уровня значимости, обозначаемого α. Если α = 0,005, то это означает 0,5-процентную ошибку или 99,5%-ю уверенность в результатах анализа. Так например, для данных, приведенных в табл.5.9 вычисленная величина χ² – критерия оказалась близкой к 4, а табличное значение критерия при α = 0,005 и числе степеней свободы k–3=4 составляет 9,5. Поэтому гипотеза о нормальности полученного экспериментально распределения оправдывается с 99%-й уверенностью. Еще одно уточнение связано с тем, что критерий Пирсона хорошо «работает» при достаточно большом наборе экспериментальных данных (n ≥ 50) и частотах в различных интервалах не меньше 5. В соответствии с этими рекомендациями количество интервалов k в рассматриваемом примере оказалось равным 7, а число степеней свободы 4.

Согласование в системе из двух наборов случайных величин {x_i} и {y_j} может быть обнаружено в рамках корреляционного анализа, в основе которого лежит гипотеза о связи между двумя признаками. Один из признаков – факторный (условно, определяющий), а другой – результативный. Рассмотрим процедуру поиска корреляционной связи на конкретном примере. Табл.7.1, 7.3 (Приложение) задают два набора СВ: сгруппированные данные по затратам фирм на рекламу {x_i} и среднее количество туристов в году {y_j}, воспользовавшихся услугами этих групп фирм (всего 20 пар значений). Диаграмма, изображенная на рис.7.1 (Приложение) представляет эти данные в корреляционном поле величин x и y. Усредняя данные по величинам y для различных фирм, затративших на рекламу одинаковые средства х, можно построить эмпирическую линию связи между х и y (так называемую, линию регрессии), подобрать теоретические коэффициенты линии связи и убедиться в наличии зависимости числа клиентов фирм от затрат на рекламу.

Можно также рассчитать для нормированных значений и

среднее нормированное отклонение произведения этих величин с помощью коэффициента Пирсона – линейной корреляции r_xy :

.

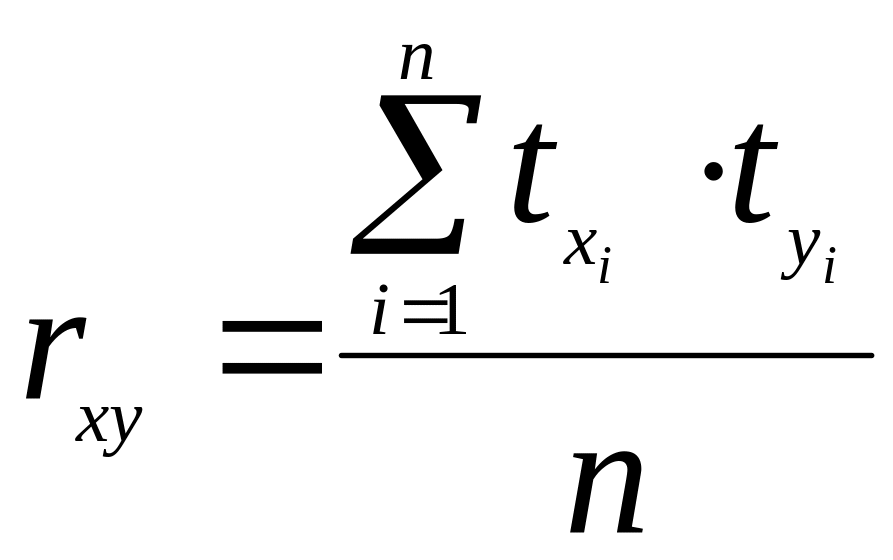В рассматриваемом примере величина коэффициента линейной корреляции, равная r_xy = 0,8105, свидетельствует о возможном наличии прямой корреляционной связи между факторным и результативным признаками. При величине r_xy ,близкой к 0 такая связь не проявляется. Существуют и другие способы оценки связи между случайными величинами.

В том случае, когда исследуемые признаки не имеют количественной меры, может быть использовано экспертное ранжирование. Табл.7.7 (Приложение) представляет сравнительные данные по экспертной оценке рангов кандидатов в депутаты и по количеству поданных за каждого из них голосов избирателей на выборах. Исходя из дисперсии величины разности между рангами х и у, то есть из формулы: где величина а величина n – количество рангов (степеней свободы), Спирмэн получил окончательную формулу для коэффициента ранговой корреляции в виде:

.

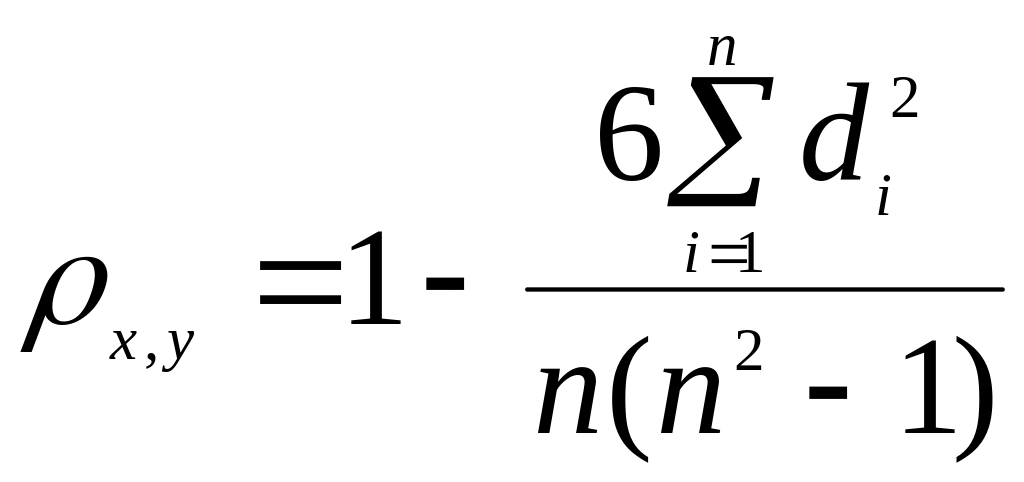В рассматриваемом примере коэффициент ранговой корреляции оказался равным 0,758. Так как значения ρ заключены в пределах от –1 до +1, то в данном случае можно предположить наличие прямой зависимости между оценками экспертов и результатами выборов. Однако, при таком небольшом объеме выборки (мало степеней свободы) согласие между величинами х и у можно утверждать только не более чем с 95%-й уверенностью, так как соответствующее табличное значение ρ (см. справочники по математической статистике) равно 0,636. В то же время, при 99%-й уверенности ρ_теор = 0,7818, что больше полученного в эксперименте коэффициента Спирмэна и, следовательно, корреляция между рангами может оказаться случайным совпадением.

Исследования изменений статистических показателей с течением времени приводят к статистическим закономерностям, выраженным в виде рядов динамики. Так, например, результатом таких исследований, проведенных органами статистики, явилась табл. 8.4 (Приложение), касающаяся динамики среднемесячной заработной платы в России за 1995 год. Проведение подобных исследований за последующие годы может определить тенденцию развития страны. Аналогично, можно использовать ряды динамики не только в макроэкономике, но и по отношению к небольшим предприятиям и организациям. На рис.8.4 представлен ряд динамики выпуска продукции (в денежном выражении) некоторым предприятием. Скачкообразный характер распределения переменной (млн. руб.) во времени не позволяет сразу оценить тенденцию развития предприятия. Для определения закономерности в работе (стабильности, повышения или снижения показателей, ритмичности и т.п.) используется метод выравнивания ряда динамики, основанный на усреднении данных по укрупненным интервалам. Действительно, так как среднее значение СВ всегда находится между максимальным и минимальным ее значением, то ряд, построенный по средним значениям в укрупненных интервалах, будет характеризоваться меньшими отклонениями (флуктуациями) признака. Процедура выравнивания продемонстрирована на том же графике для укрупненных 3-х дневных и 5-ти дневных скользящих средних. Скользящими они называются потому, что интервалы перекрываются и сдвигаются на один день. При этом количество интервалов не уменьшается по сравнению с исходным графиком.

Еще один пример приведен на рис.8.8 (Приложение), касающийся товарооборота специализированного магазина одной зарубежной фирмы за 1991 – 1995 годы. На диаграмме видно, что скользящая квартальная средняя ведет себя периодически и имеет среднюю линию развития (линию тренда). Следовательно, товарооборот магазина в среднем растет линейно с течением времени. Скорость роста характеризуется коэффициентом роста k = 0,158, то есть тангенсом угла наклона линии тренда к оси времени.

Очевидно, в реальной жизни встречаются и другие математические функции, описывающие кривую тренда рядов динамики, а подобный анализ поведения систем во времени может быть использован не только в экономике, но и в психологии, педагогике, естествознании, социологии, политике и других сферах человеческой деятельности. Соответственно, можно говорить об экономической, естественнонаучной, педагогической, психологической социальной и др. статистике.