Тема 3. Статистические распределения.

Если случайным событием при испытаниях по исследованию признака или свойства процесса является получение численных значений этого признака, то говорят о наборе случайных величин (СВ), так как каждое число из набора возможных значений может появиться, а может не появиться в результате проведенного эксперимента. Если СВ принимает любые значения на числовой оси или в заданном условиями интервале, то говорят о непрерывной случайной величине, если же значения определенные, то есть заданы ограничения, то СВ – дискретна. Рассмотрим примеры задания случайных величин.

1. Числа от 1 до 6, нанесенные на гранях куба (гексаэдра) являются примером дискретной случайной величины, если куб использовать в качестве игральной кости (рис.4.1 представляет развертку куба на плоскости).

2. При игре в «Дарс» дискретные величины – это цифры на мишени, фиксируемые случайным образом при бросании «пера» (рис.4.2).Если же на мишени стереть все границы полей, то координаты (x,y) точки А – конца застрявшего пера, будут непрерывными СВ (рис.4.3, т.А).

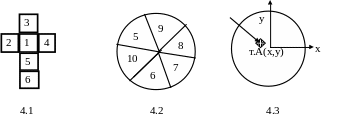
Рис. 4. Примеры случайных величин

Если для каждого значения СВ удается найти соответствующую вероятность, то совокупность этих значений и соответствующих им вероятностей называют распределением вероятностей. В этом случае распределение можно представить в виде таблицы (табл.6).

Таблица 6

Распределение для СВ

Р аспределение общего вида на грани куба

СВ X x₁ x₂ x₃ …….x_i… x_i 1 2 3 4 5 6

Вероятность р р₁ р₂ р₃ …….р_i… р_i 1/6 1/6 1/6 1/6 1/6 1/6

Очевидно, что для непрерывной СВ вероятность появления ее точного значения всегда равна нулю, так как она вычисляется отношением нулевых размеров точки к размерам площади не равной нулю. Поэтому имеет смысл сравнивать размеры хотя бы малой площади или интервала Δx к размерам площади или к размерам оси, соответствующим полной группе событий. Если обозначить Δр – вероятность попадания случайной величины x в интервал ее значений Δx, то можно рассчитать вероятность, соответствующую единичному интервалу значений СВ, т.е. вычислить отношение Δр/Δx. По смыслу, данное отношение является плотностью вероятности, которую обозначим символом функции f(x). Наконец, для детального описания необходимо приблизить границы интервала Δx к точке x. При этом, размеры интервала станут бесконечно малыми, но и соответствующая вероятность попадания СВ в этот интервал станет меньше. Тогда можно найти предел отношения Δр/Δx при Δx → 0, и если такой предел существует, то по смыслу он будет характеризовать плотность вероятности, но уже в точке x, принадлежащей бесконечно малому интервалу dx, что кратко запишем следующим образом:

.

С другой стороны, если этот предел существует, то, как было определено в §6, он называется производной и обозначается dp/dx, то есть f(x) = dp/dx. При такой записи каждому бесконечно малому интервалу dx можно поставить в соответствие величину dp – вероятность попадания СВ в этот интервал: dp = f(x)dx. Поэтому функцию f(x) также называют распределением, точнее, дифференциальной функцией распределения вероятностей, но по смыслу плотность вероятности f(x), как и выше, характеризует вероятность появления случайной величины в единичном интервале ее значений.

Для небольших интервалов Δx можно считать, что f(x) практически не меняется на этом интервале и можно записать: Δр = f(x)Δx. Пример, изображенный на рис.6 демонстрирует результат построения распределения f(x), где случайной величиной x является координата точки мишени, а вероятность Δр определяется экспериментально частотой, т.е. количеством точек с координатами, попадающими в Δx случайным образом.

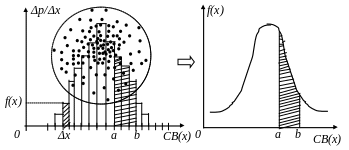
Рис.6. Построение распределения

Из рисунка видно, что вероятность Δр=f(x)Δx численно равна площади заштрихованного столбика и это можно отнести не только к интервалу Δx, но и к любому другому интервалу значений СВ, используя теорему сложения вероятностей для несовместных событий. Если ступеньки станут очень частыми, т.е. когда в пределе Δx можно заменить на dx, экспериментальная диаграмма перейдет в график идеальной функции плотности вероятности, как это представлено на рис.6 (справа). Среди многих функций плотности вероятности распределение, изображенное на рис.6 встречается очень часто и аналитически график этой функции записывается в виде:

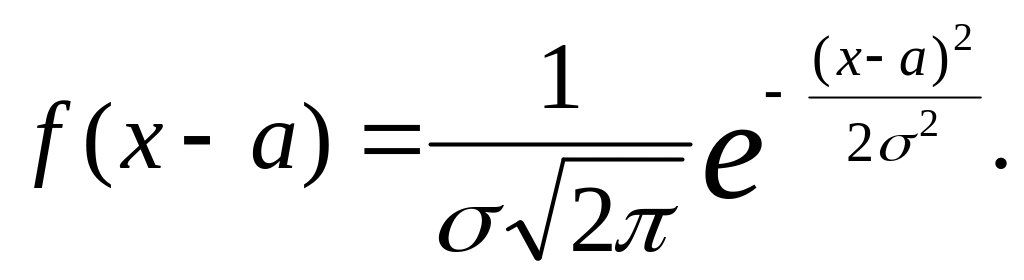
Данная функция исследована в рамках математики Гауссом, носит его имя и называется в теории вероятностей нормальным распределением. Входящие в него величины a и σ являются параметрами распределения, а π и е – иррациональные числа.

Рассмотрим полученное распределение вероятностей и выясним его основные характеристики (рис.7).

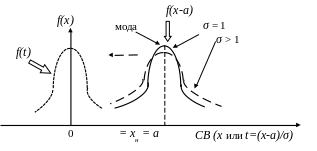
Рис.7. Нормальное распределение

Так как у плотности вероятности f(x) есть максимум, то соответствующее этому максимуму наиболее вероятное значение СВ называют модой.

Так как функция f(x) симметрична, то очевидно, что вычисление среднего значения x (обозначается , x_ср или <x>) совпадает c линией симметрии.

Если в нормальном распределении сделать замену переменных и ввести новую величину t=(x-a)/σ, т.е. из каждого значения случайной величины x вычесть а, то получится функция

, смещенная в начало координат, так как теперь ее максимум будет совпадать с началом координат (при t=0). Но максимум функции f(t) совпадет с максимумом f(x), только если а = 0. Это означает, что величина а характеризует положение центра симметрии, т.е. вместе с этой величиной меняется и среднее значение СВ. Поэтому x_ср = а.

Функция f(t) отличается от f(x) еще и тем, что параметр σ принял значение равное 1. Поэтому, если в распределении f(x) величина σ будет больше 1, то в максимуме функции (при x = a) коэффициент перед экспонентой е уменьшится и график в точке x = a пройдет ниже, чем при σ = 1. Этот факт будет означать, что доля значений СВ близких к х_ср уменьшилась и, следовательно, увеличилась доля значений СВ далеких от х = а. В этих интервалах график f(x) пройдет (см.рис.7) выше исходного графика (с σ = 1). В результате, разброс СВ от среднего значения возрастет. Поэтому величина σ является мерой разброса или среднеквадратичным отклонением случайной величины от ее среднего значения и называется также стандартным отклонением. Так как в показателе степени функции Гаусса фигурирует σ² , то и эта величина является параметром распределения и называется дисперсией (D). Можно записать, что σ = .

Теперь научимся рассчитывать средние характеристики распределений. Начнем с простого примера. Для того, чтобы вычислить среднее значение СВ, появляющейся в результате бросания игральной кости в форме кубика, очевидно, необходимо просуммировать числа, нанесенные на гранях и разделить на общее число граней. Тогда имеем:

и, учитывая, что х₁ =1, х₂=2,…, х₆ = 6, а р₁ = 1/6, р₂ = 1/6, …, р₆ = 1/6, можно записать формулу для вычисления среднего значения (его называют математическим ожиданием СВ):

,

где i – индекс суммирования по всем значениям СВ.

Если количество случайных событий равно , вероятность появления каждого из них определяется как р_i = m_i/n, а общее число событий равно , то среднее значение СВ , или, окончательно имеем:

.

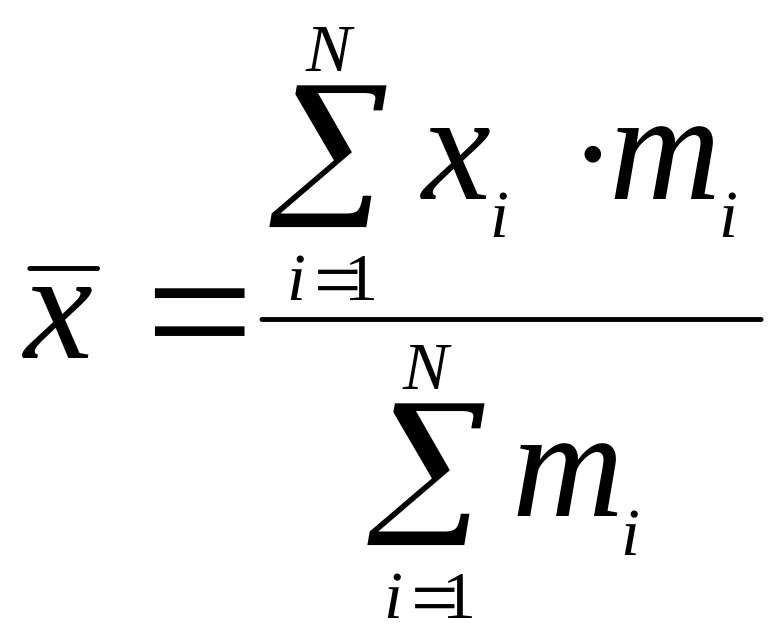Если теперь на гранях кубика вместо каждого значения СВ запишем величину, возведенную в квадрат, то для среднего значения новой случайной величины получим:

, или в общем случае, имеем:

.

Получили формулу для вычисления среднего значения квадрата случайной величины. Рассуждая аналогичным образом, можно вычислить и дисперсию случайной величины, как ее среднеквадратичное отклонение от среднего значения. В этом случае имеем:

Далее, можно вычислить среднекубическое отклонение СВ и среднее значение четвертой степени отклонения от х_ср:

,

Для непрерывных случайных величин формулы средних значений трансформируем следующим образом:

• вместо x_i записываем текущую координату х;

• вместо вероятности р_i записываем dp=f(x)dx, т.е. вероятность попадания в бесконечно малый интервал dx значений СВ;

• вместо суммы 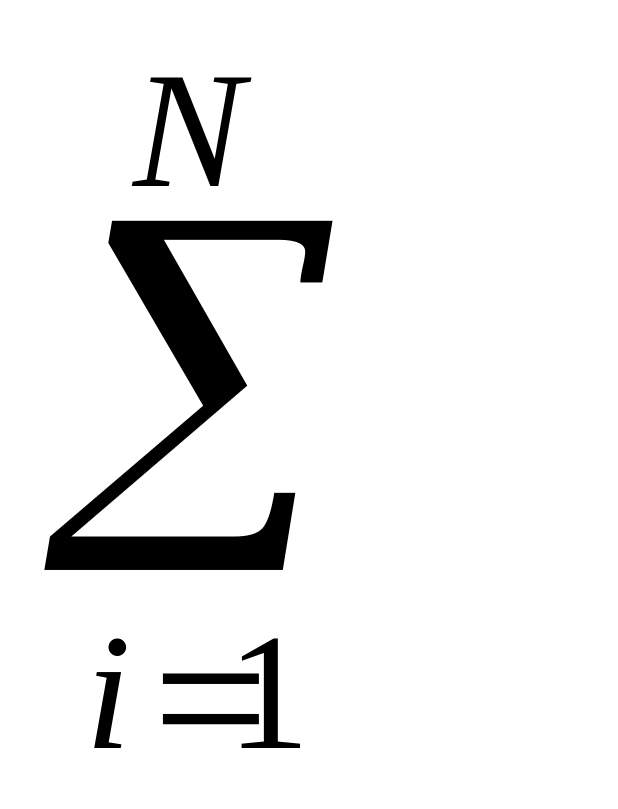вводим сумму бесконечно малых величин 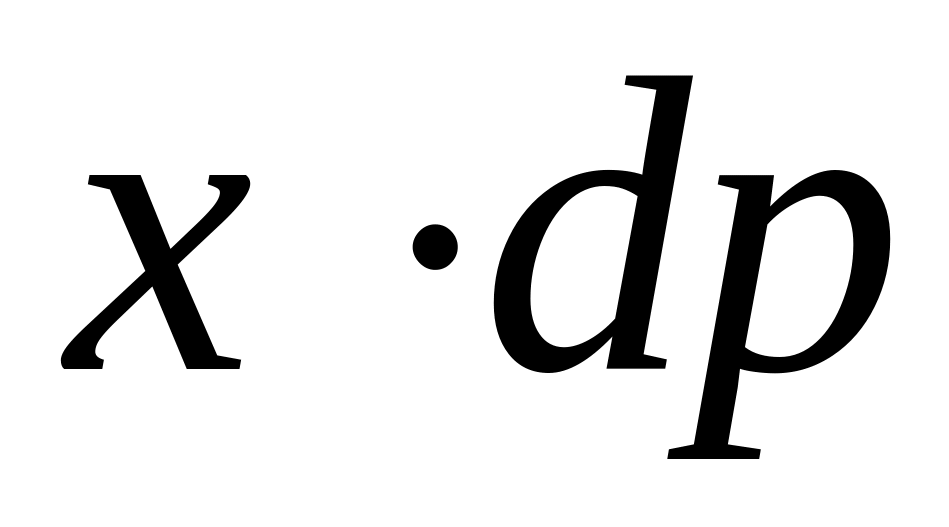, которая, как известно, называется интегралом.

В результате имеем еще один набор формул для вычисления средних значений случайной непрерывной величины.

;

;

;

;

.

Для нормального распределения х_ср= а, D =σ² , μ₃=0, μ₄=3. Для других распределений величину μ₃/σ³=As называют коэффициентом ассимметрии и этот коэффициент тем больше, чем значительнее нарушена симметрия распределения по сравнению с нормальным. Величину, равную μ₄/σ⁴ –3=Эк называют эксцессом. Эта величина также характеризует нарушение формы кривой («островершинность» или «плосковершинность») по сравнению с нормальным распределением.

При переходе от теоретически рассчитанных вероятностей к частотам, получаемым в эксперименте, важно понять различие между «частотной» плотности вероятности f(x)=Δp/Δx и функцией плотности f(x)=dp/dx. В первом случае, вероятность Δp=f(x)Δx геометрически соответствует размерам площади под графиком (см. рис.6), опирающейся на интервал Δx, а во втором, размеры этой площади бесконечно малы. Так как СВ может попасть или в один интервал Δх₁ , или в соседний –Δх₂ , или…и т.д., то для поиска вероятности попадания величины х в относительно большой интервал (от а до в на рис.6), необходимо воспользоваться теоремой сложения вероятностей для несовместных событий (если считать, что СВ не может попасть сразу в несколько интервалов). Сложение же бесконечно малых dp, как мы уже говорили ранее, требует умения решать интегралы от функции распределения в заданных пределах. С другой стороны, оценка величины соответствующей вероятности может быть сделана, как в теоретическом, так и в эмпирическом распределении, по размерам площади «столбиков», опирающихся на интервал от а до в (рис.6). Отдельные этапы построения распределений можно понять, анализируя таблицы 3.4, 5.1, 5.2, 5.3 и соответствующие им графики на рис.5.3 (полигон частот) и рис.5.4 (гистограмма), представленные в Приложении II.

По теореме полной вероятности сумма всех вероятностей (всех площадей) должна характеризовать вероятность достоверного события, т.е. равняться единице, а тогда и интеграл =1. (Последнее выражение называют условием нормировки функции плотности вероятности). Однако, если экспериментальные данные оказались ограниченными между точками х_Н -нижней границей экспериментальных данных и х_В – верхней границей, то и на графике функции f(x) площади, расположенные под графиком слева от нижней границы и справа от верхней в расчетах не участвуют (отброшены). Поэтому вся площадь под кривой распределения уже не соответствует 100% возможностей, а размеры Δх, взятые от т.Н до т.В определяют так называемый доверительный интервал. Если например, в нормальном распределении доверительный интервал ограничен точками х_Н=х_ср–σ и х_В=х_ср + σ, то площадь под графиком составляет 68,3% от всей площади под кривой (соответственно, вероятность р(–σ<х–х_ср<+σ)= 0,683). Если х_Н=х_ср­– 2σ и х_В=х_ср+2σ, то размеры площади «доверия» составляют 95,4%, а при отклонениях х от х_ср равных ±3σ вызывает наибольшее доверие, т.к. соответствующая площадь составляет величину 99,7% от полной площади под кривой распределения.