Раздел 7. Уравнения кривых второго порядка.

Кривые второго порядка, описываются уравнениями второй степени с двумя переменными. К ним относятся:

(1). уравнение окружности: (х – х₀)² + (у – у₀)² = R², или, в частном случае, когда начало координат совпадает с центром окружности, х² + у² =R²;

(2). уравнение эллипса: ;

(3). уравнение гиперболы: .

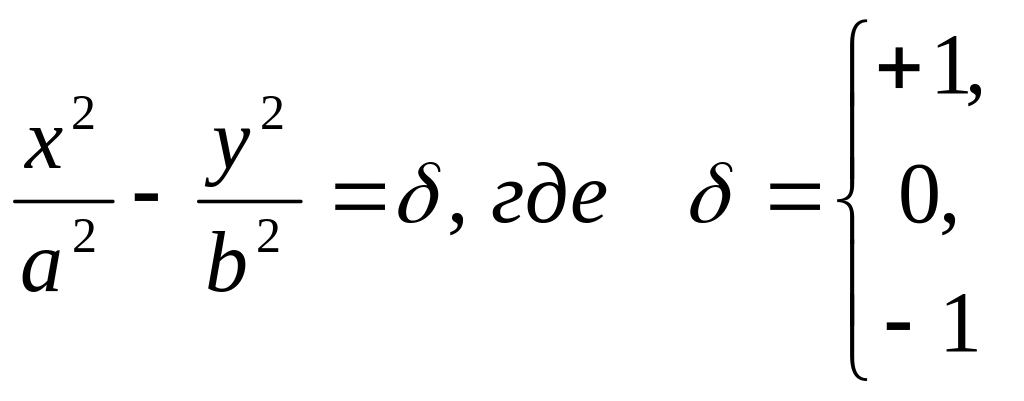Подробное описание способов построения и анализа кривых можно найти в рекомендуемой литературе (под ред. Н.Кремера).

Раздел 8. Матричные уравнения.

Появление матричного исчисления исторически явилось необходимым этапом при решении систем уравнений с большим числом переменных. В контрольной работе предлагаются задания начального этапа применения матриц к решению системы уравнений: записи системы, записи соответствующего матричного уравнения и расчета определителя матрицы. Правила нахождения определителя матрицы и основные операции матричного исчисления даются в Приложении.

Рассмотрим пример типовой задачи, которая может встретиться в контрольной работе.

Записать матричное уравнение и вычислить определитель матрицы для системы уравнений:

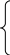х₁+2х₂+ 3х₃+4х₄ = 4,

2х₁+3х₂+4х₃+х₄ = –1,

3х₁+4х₂+х₃+2х₄ = 3,

4х₁+х₂+2х₃+3х₄ = 5.

Коэффициенты при неизвестных (х₁, х₂, х₃, х₄) являются соответствующими элементами матрицы, поэтому можно записать:

.

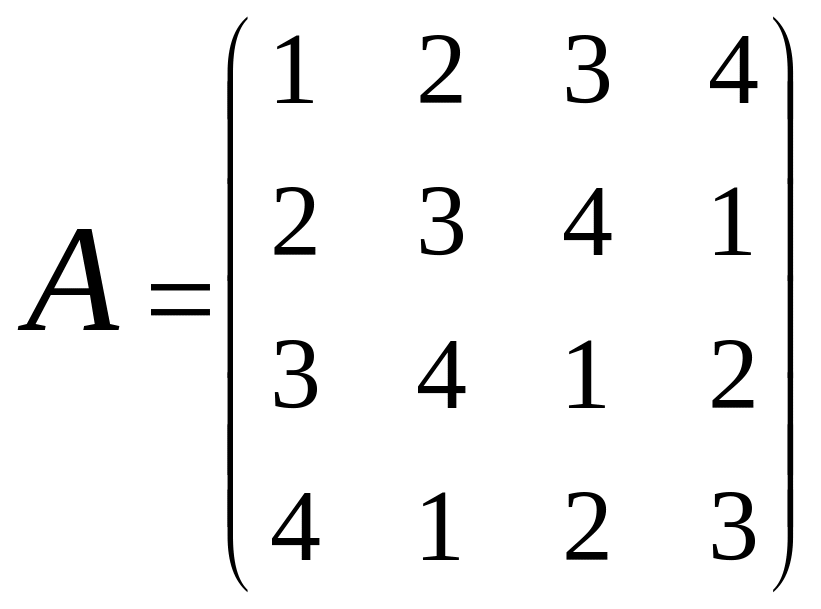Все переменные в заданной системе уравнений образуют вектор – столбец, который в матричной форме можно записать следующим образом:

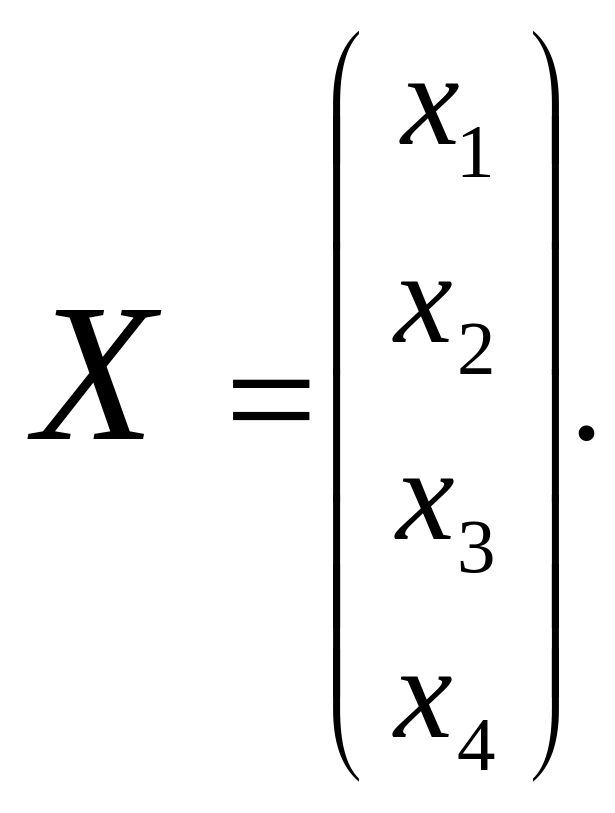
Результат действия матрицы А на вектор Х также можно изобразить в виде вектора – столбца, определяемого свободными членами в заданном уравнении:

.

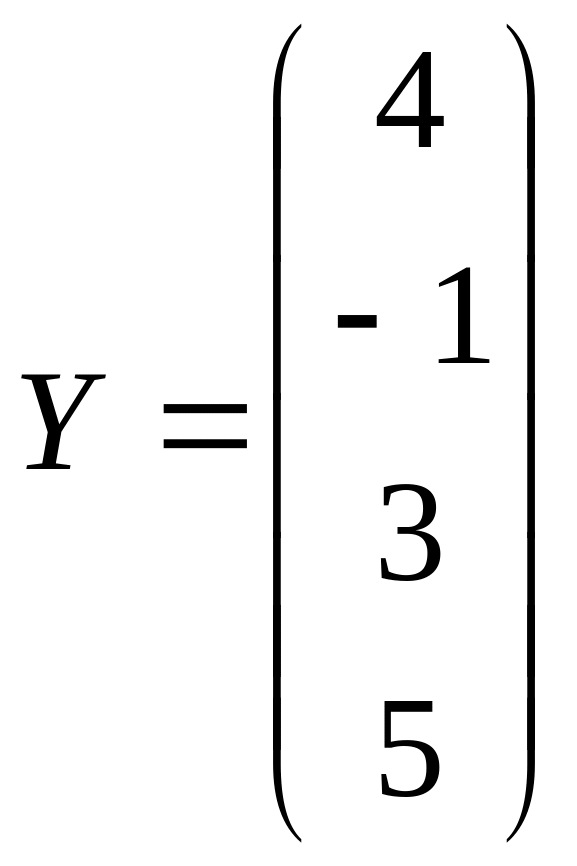Поэтому системе уравнений в задаче соответствует матричное уравнение:

AX = Y.

Теперь вычислим определитель Δ матрицы А:

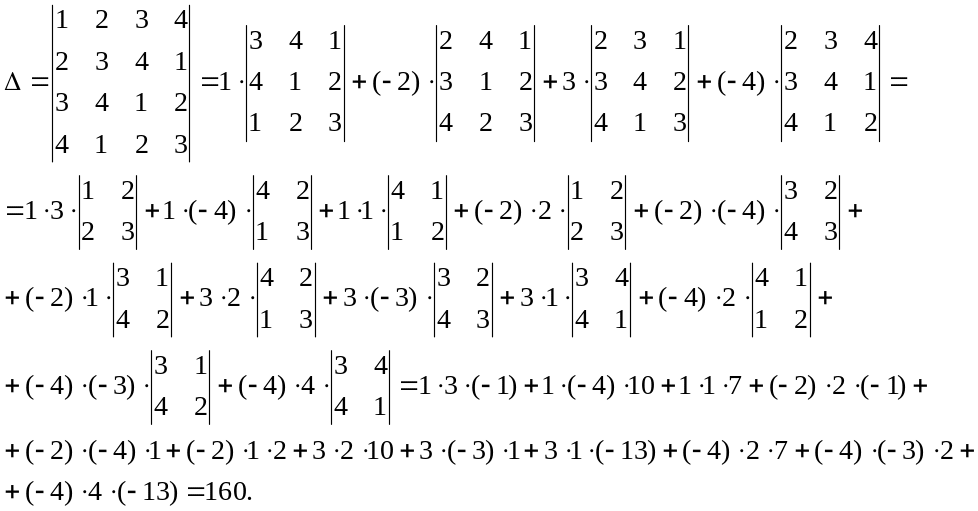
Задача решена.

П Р И Л О Ж Е Н И Я I

I. Операции с показательными функциями:

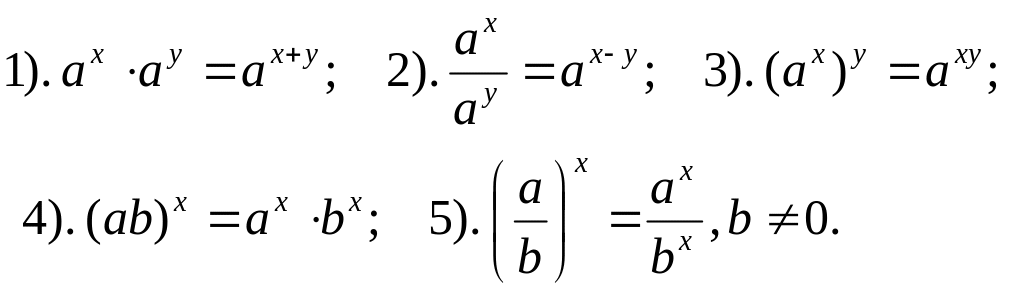
II. Операции с логарифмическими функциями:

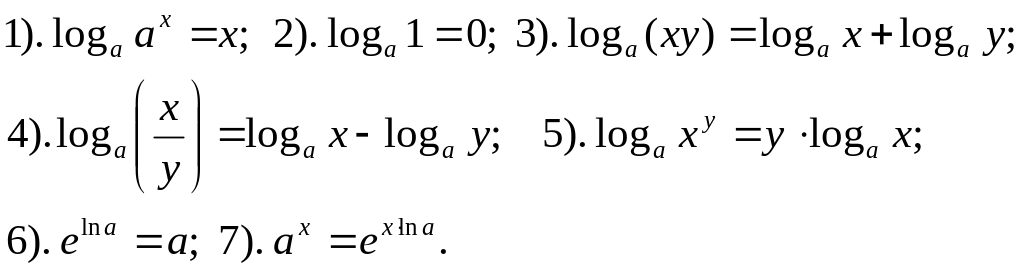
III. Свойства пределов и операции с пределами:

IV. Таблица производных:

1). У = С, у’= 0; 2). У = х, у’ = 1; 3). У = f(x) + g(x), y’ = f ’ + g ’ ;

4). Y = f(x)g(x), y’ = f ’g + f g ’; 5) y = Cf(x), y’ = Cf ’;

6). ; 7). ;

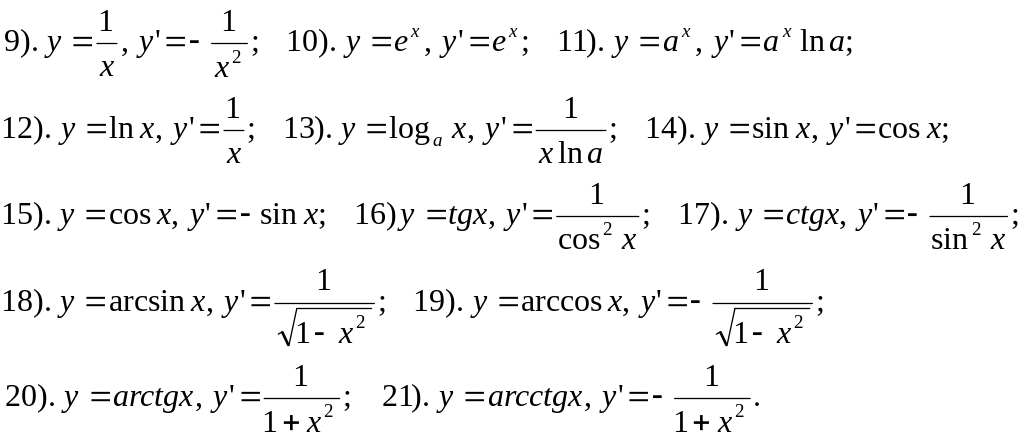Дифференцирование сложной функции производится следующим образом:

для y = f[u(x)] производная y’= f’(u)u’(x).

V. Свойства неопределенных интегралов:

(1).

Таблица неопределенных интегралов:

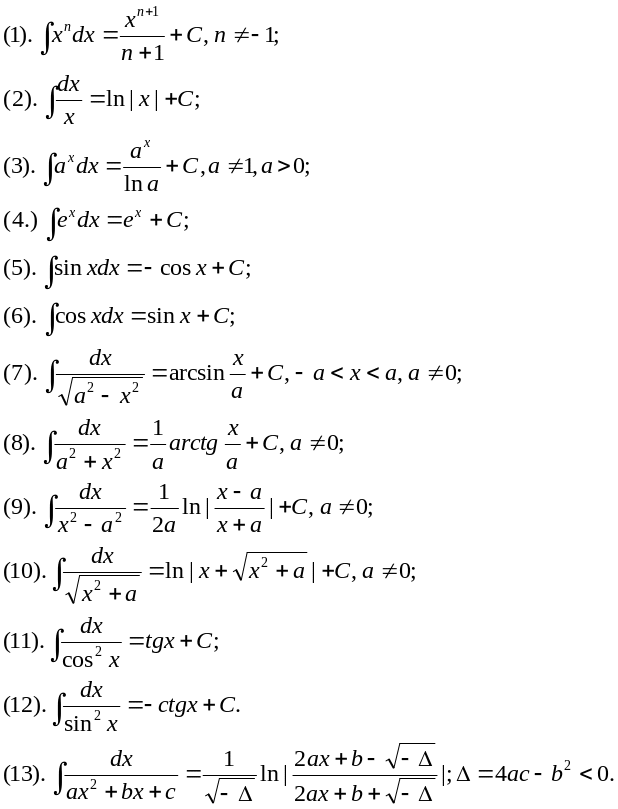
VI. Операции над матрицами.

1. Умножение матрицы на число: В = λА ↔ (b_ij = λa_ij ). Стрелка↔ означает переход от операций, записанных для матриц к соответствующим операциям с матричными элементами (и обратно).

2. Сложение матриц: С = А + В ↔ (c_ij = a_ij + b_ij) . Матрицы должны иметь одинаковый размер.

3. Вычитание матриц: C = A – B = A + (–1)B.

4. Умножение матриц. Эта операция определена только тогда, когда число столбцов (k) первой матрицы А(m×k) равно числу строк (k) второй матрицы В(k×n). Образующаяся при произведении матрица С, имеет m – строк и n – столбцов, то есть ее можно записать: C(m×n).

С = А×В = АВ ↔ c_ij = a_i1b_1j + a_i2b_2j + …+ a_ikb_kj (i = 1,2,..,m; j = 1,2,..,n).

При умножении матриц произведение АВ не всегда равно произведению ВА. Если можно записать: АВ = ВА, то матрицы А и В – коммутативны (перестановочны), если АВ ≠ ВА, то матрицы некоммутативны.

5. Транспонирование матрицы: Эта операция означает замену строк матрицы на столбцы, тогда каждому элементу a_ij исходной матрицы соответствует элемент a_ji в транспонированной матрице.

Транспонированная матрица обозначается А’ или А^Т.

6. Если в исходной квадратной (m×m) –матрице вычеркнуть одну строку и один столбец, то оставшиеся элементы образуют новую матрицу, «дополнительную» к элементу матрицы, лежащему на пересечении вычеркнутой строки и столбца. Для этой новой матрицы можно продолжить процедуру вычеркивания, пока матрица не окажется простейшей, состоящей из двух строк и столбцов:

М = .

Число Δ = |A| = a₁₁a₂₂ – a₁₂a₂₁ называется определителем матрицы второго порядка. Можно умножить определитель на элемент a_ij из матрицы более высокого (третьего) порядка, к которому матрица была дополнительной и получить новое число, которое называется минором M_ij элемента a_ij, а минор, взятый со знаком (–1)^i+j называется алгебраическим дополнением A_ij этого элемента.

A_ij = (–1)^i+j M_ij.

Тогда для любой квадратной матрицы можно вычислить определитель, используя теорему Лапласа: Определитель квадратной матрицы равен сумме произведений элементов любой строки (или столбца) на их алгебраические дополнения.

Δ = a_i1A_i1 + a_i2A_i2 + …+ a_inA_in .

Для того, чтобы при записи отличить матрицу от определителя этой матрицы, определитель часто записывается как модуль величины вертикальными линиями:

.

Л И Т Е Р А Т У Р А

1. Высшая математика для экономистов (под ред. Н.Ш.Кремера).

М.: Изд. Объедин. «ЮНИТИ». 1999 (2000). 471с.

2. А.Н.Колесников Краткий курс математики для экономистов.

М.: ИНФРА-М , 2001.208с.