Раздел 5. Найти неопределенный интеграл.
Перед решением задач этого раздела необходимо внимательно изучить свойства интегралов, а при решении иметь перед собой список табличных интегралов от элементарных функций. Информация по свойствам и решению табличных интегралов дается в Приложении к данной методической разработке.
Все основные методы решения интегральных задач основаны на поиске такого приема, который позволяет свести исходный интеграл к табличному или сумме табличных интегралов. Сюда относится: (1) – разложение подинтегральной функции на сумму более простых, которые легче свести к табличным; (2) – замена переменных, приводящая интеграл к табличному; (3) – интегрирование функции по частям. Во всех случаях следует, по возможности, упрощать вид подинтегральной функции. Рассмотрим применение методов решения интегралов, то есть поиска «первообразной» функции на конкретных примерах.
(1):
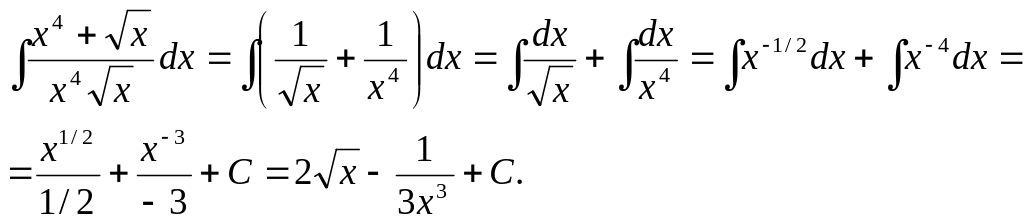
Применен метод разложения подинтегрального выражения.
(2):
.
Упрощение подинтегральной функции привело к табличному интегралу.
(3):
Использовано упрощение и разложение подинтегральной функции.
(4):
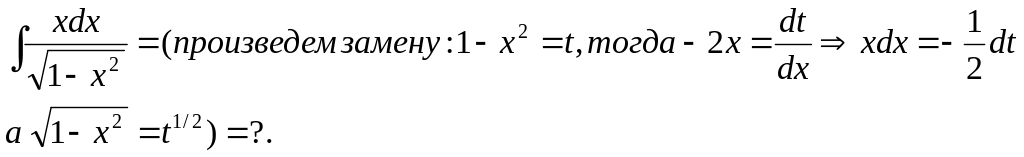
После подстановки в подинтегральное выражение рассчитанных величин, получим:
.
(5):
.
При решении произведена замена переменных:
.
Полученное выражение и было подставлено
под интеграл.
(6):
Найти
.
Для решения обозначим x = u, а v = sin x. Тогда dv = cosx dx , а dx = dv. Исходный интеграл будет выглядеть следующим образом:
.
Применен метод решения по частям. Из
этого примера видно, что интегрирование
по частям применяется в том случае,
когда подинтегральная функция представляет
собой произведение
двух функций.
(7):
Найти
.
Введем функцию u = x-2, для которой -2x-3dx = du. Отсюда, стоящее под интегралом выражение dx/x3 можно заменить на - du/2. Обозначая ln x = v, получим подинтегральное выражение в форме, к которой применим метод интегрирования по частям:
.
Величина d(ln x) = dx/x и после ее подстановки под интеграл, получим:
.
Раздел 6. Вычисление определенных интегралов.
Методы
вычисления определенных интегралов
основываются на поиске первообразной
функции, как это делается в случае
решения задач с неопределенными
интегралами, и последующим применением
формулы подстановки пределов
интегрирования, называемой формулой
Ньютона – Лейбница:
.
Рассмотрим несколько примеров применения этой формулы.
(1):
.
(2):
.
В этом примере использовано решение по частям неопределенного интеграла, заданного в примере (7) предыдущего раздела.
Часто (например, при обработке статистических данных) вычисление определенного интеграла бывает связано с поиском площади фигуры, ограниченной известными функциями. Рассмотрим один такой пример.
(3):Вычислить
площадь фигуры, ограниченной линиями:
x=
,
х
= 0, у =
Данные этой задачи представим графически (рис. 5).
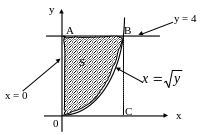
Рис. 5. К задаче (3)
Из
рисунка видно, что площадь S
= S0ABC
– S0BC
. Для вычисления площади прямоугольника
0АВС необходимо знать координаты точек
А и В. Прямые у = 4 и х = 0 , на пересечении
которых лежит точка А, определяют ее
координаты: А(0,4). Координата «у» точки
В также определена прямой у = 4, а ее «х»
– координата может быть найдена из
совместного решения системы уравнений:
, так как эта точка находится на пересечении
линий, соответствующих этим уравнениям.
Простая подстановка верхнего уравнения
в нижнее дает х = 2. Тогда точка В имеет
координаты В(2,4). Расстояние 0А = 4ед., а
расстояние АВ = 2ед., поэтому площадь
S0ABC
= 8ед.2
Далее, исходя из геометрического смысла
определенного интеграла, площадь
криволинейного треугольника 0ВС следует
искать с помощью интегрирования в
пределах от х = 0 до хмакс=
2:
.
Окончательный ответ S
= 8 – 8/3 = 16/3.