Раздел 3. Найти пределы функций.

Этого вида задачи решаются несколькими различными приемами.

(1). Сведением пределов заданных функций к двум «замечательным» пределам, для которых известен результат расчета. Первый замечательный предел имеет следующий вид: , а второй записывается так: . Иногда считают, что второй предел является определением числа е – основания натуральных логарифмов. Второй замечательный предел после замены переменного у = 1/х можно представить в другой форме, которая также используется при решении задач: .

(2). Функция, предел которой следует определить, часто представляет собой отношение двух степенных функций общего вида (двух многочленов). Эти отношения после подстановки в них значения бесконечного предела, к которому стремится аргумент (х → ∞) представляют собой неопределенности вида .

Можно показать, что такие задачи решаются делением числителя и знаменателя на х^k, где k – наибольший показатель степени в многочленах.

(3). Если аргумент стремится к какому – либо конечному пределу, то необходимо подобрать такую замену переменных, чтобы изменить соотношение величин показателей степени многочленов в числителе и знаменателе.

(4). Наконец, для раскрытия неопределенности вида [∞ – ∞] используется прием умножения разности функций (f – u) на сопряженное выражение: (f + u).

(5). Иногда, при поиске предела отношения двух произвольных функций используется прием разложения функций в соответствующие степенные ряды. Полезно также применять, так называемое, правило Лопиталя: предел отношения двух бесконечно малых или бесконечно больших функций равен пределу отношения их производных.

Рассмотрим несколько конкретных примеров на вычисление пределов. При решении задач необходимо знать операции, которые можно производить с пределами (см. Приложение I).

(1): .

.

(2): .

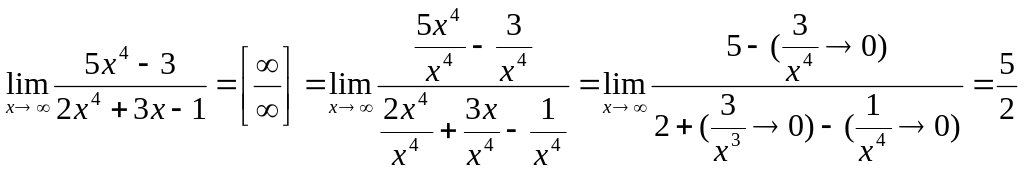(3):

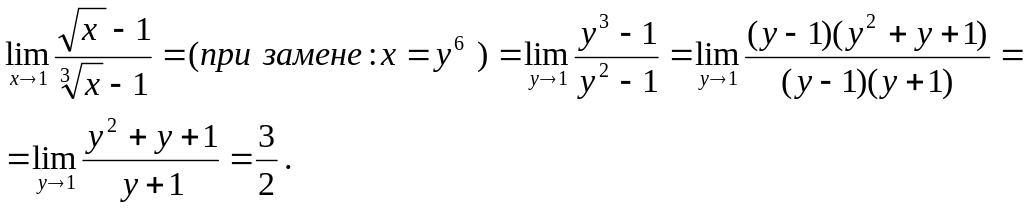
(4):

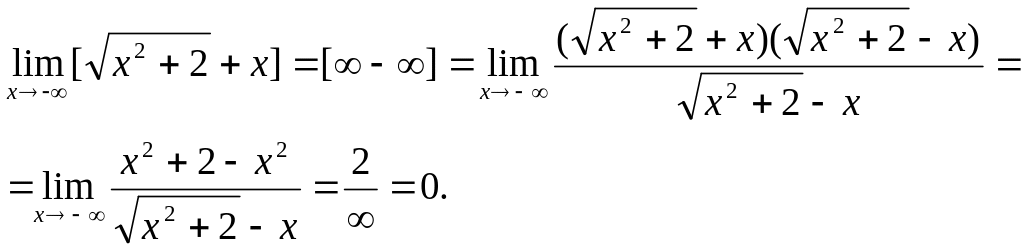
(5): .

Первый шаг применения правила Лопиталя не привел к разрешению

неопределенности. Применим это правило к полученному пределу еще раз:

.

Раздел 4. Вычисление производных.

Для решения задач на вычисление производных необходимо иметь справочный материал по результатам таких вычислений для простейших функций (см. Приложение), знать основные правила вычислений от произведения функций, от отношения функций, от степенных функций и от сложных функций. Основные правила взятия производных также представлены в Приложении.

Рассмотрим несколько типовых примеров вычисления производных от функций, которые могут встретится при выполнении контрольной работы.

(1): у = e^xsin x. y’ = (e^x)’sin x + (sin x)’e^x = e^xsin x + e^xcos x = e^x(sin x + cos x).

Использовалось правило дифференцирования произведения двух функций.

(2): . Использовано правило дифференцирования отношения двух функций.

(3): у = 5х⁴ – 3х² +2х – 1. у’ = 5∙4x³ – 3∙2x + 2 = 20x³ – 6x + 2. Использовано правило дифференцирования суммы степенных функций.

(4): у = ln |sin x|,x≠ 2kπ .Обозначим u = sin x.Тогда y = ln u(x).у’=(ln u)’ = . Использовалось правило дифференцирования

сложной функции.

(5):

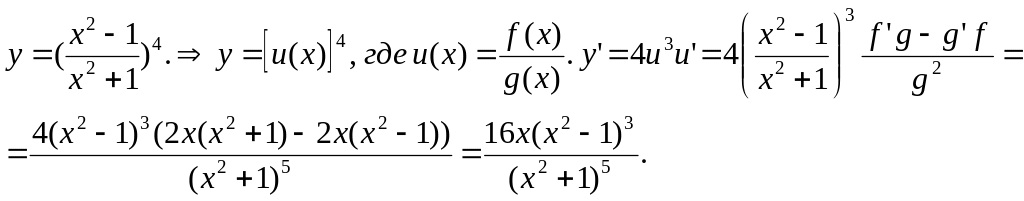
(6): у = х^х . Прологарифмируем обе части равенства: ln y = xln x. Теперь возьмем производные от обеих частей: (ln y)’ = x’ln x + x(ln x)’, откуда следует:

. Из полученного равенства выражаем производную у’:

у’ = y(ln x + 1) = x^x(ln x + 1).

(7): у = а^х. Применяя к заданной функции тот же подход, что и в предыдущей задаче, получаем: ln y = xln a, (ln y)’ = ln a, y’/y = ln a, y’ = = a^xln a.