В.Г. РАУ

КРАТКИЙ КУРС МАТЕМАТИКИ

И ОБЩЕЙ ТЕОРИИ СТАТИСТИКИ

Д ЛЯ ГОСУДАРСТВЕННЫХ СЛУЖАЩИХ

И ПРЕДПРИНИМАТЕЛЕЙ

2005

РОССИЙСКАЯ АКАДЕМИЯ ГОСУДАРСТВЕННОЙ СЛУЖБЫ

(Владимирский филиал)

Экзаменационные вопросы по курсу математики

(1-й курс на базе среднего и среднего специального образования)

Основной курс:

1. Множества и операции над ними.

2. Понятие функции. Линейные функции и их графики.

3. Понятие функции. Квадратичные функции и их графики. Степенные функции.

4. Показательные, экспоненциальные и логарифмические функции. Их графики.

5. Тригонометрические функции. Их графики.

6. Понятие предела функции. Вычисление пределов.

7. Понятие производной и ее смысл.

8. Исследование функций на экстремум.

9. Правила дифференцирования. Дифференцирование сложной функции.

10. Производные высших порядков.

11. Неопределенный интеграл. Понятие о первообразной.

12. Правила интегрирования. Интегрирование по частям и с помощью замены переменных.

13. Определенный интеграл. Вычисление площадей. Формула Ньютона – Лейбница.

14. Понятие о дифференциальных уравнениях.

Приложения: (значком (*) отмечены вопросы самостоятельной работы).

1. Векторы*. Матрицы. Системы уравнений.

2. Примеры множеств в социальной сфере и действия над ними.

3. Предельный анализ в финансово-экономической сфере. Простой и сложный процент.

4. Понятие об оптимизации социальных и экономических функций*.

5. Линейные функции в экономике.

6. Квадратичные функции и максимальная прибыль.

7. Равновесие спроса и предложения на рынке.

8. Административное управление на рынке товаров.

9. Понятие эластичности функций*.

10. Операции с матрицами в экономических расчетах.

11. Понятие о межотраслевом балансе. Уравнение Леонтьева.

12. Примеры на решение уравнения Леонтьева*.

13. Применение определенного интеграла в экономике.

14. Производственная функция. Решение дифференциальных уравнений.

Часть I. М а т е м а т и к а

ВВЕДЕНИЕ.

Математика – это наука, объектами изучения которой являются множества формализованных элементов и формальных отношений между ними. Математическая формализация приводит к тому, что появляется возможность использования математического аппарата в любой науке в качестве «языка», оптимально моделирующего как реальные, так и виртуальные системы, структуры, их состояния, а также изменения состояний (процессы). В то же время, для формализации «слов» в самой математике используются неформализованные слова естественного языка, возникающие феноменологически на основе человеческого Опыта (опыта наблюдений, опыта реальных действий, опыта мышления, интуиции). В результате, процесс формализации приводит к научному языку, возникающее слово которого представляет собой определенную «модель» соответствующего слова или группы слов естественного языка. С другой стороны, возможен и обратный процесс обогащения естественного языка, за счет генерации новой ценной информации, возникающей в рамках науки.

§ 1. Множества. Операции. Функция.

Одним из основных первичных понятий математики является понятие множества, как совокупности однородных элементов в одной системе, где однородность (симметрия) определяется по наличию единого, качественного или количественного признака. Составленный список пенсионеров, находящийся в одном из отделов администрации области, является примером множества А с конечным числом элементов {a_i}, принадлежащих А. Символически, принадлежность элемента множеству записывается следующим образом: . Очевиден и признак, по которому произошло отнесение записанных людей к этому множеству. Можно составить еще один список – участников войн (множество В с элементами {b_j}), среди которых есть и пенсионеры, но признак, по которому теперь произошло объединение совершенно другой. В то же время, список областных пенсионеров А, например, является частью общегосударственного списка P{p_k}, то есть содержится в нем в качестве подмножества. Символически, этот факт записывается таким образом: . Если, при назначении льгот, списки сливаются в один общий список D{d_i}, в котором каждый элемент d_i соответствует либо пенсионеру, либо участнику войн, без указания принадлежности к конкретному списку, то для множеств A и B в математике вводится операция объединения: . Можно говорить при этом, что множества складываются. Если в списках участников войн и пенсионеров встречаются общие фамилии, то есть существует «пересечение» фамилий, то они образуют подмножество C{c_i} этих двух списков, которое получено операцией пересечения: . При этом говорят о произведении множеств А и В. При принятии решения о доплатах к льготам, часто складывается ситуация при которой бюджетных средств в области недостаточно для обеспечения объединенного списка D и даже для списков А и В, взятых по отдельности, но для пересеченных множеств, то есть для обеспечения списка С выделенных средств может оказаться достаточно.

Операция, традиционно понимаемая как сложение, по отношению к множествам неоднозначна: важно знать пересекаются ли множества между собой или нет, другими словами, могут ли они быть совмещены. При наличии пересечения для получения результата без повторений необходимо сложить списки А и В, а затем вычесть из них одинаковые фамилии, то есть множество С.

Для наглядного представления множеств и производимых с ними операций удобно изображать элементы множества точками на плоскости, а сами множества в виде кругов, внутри которых находятся эти точки (рис.1).

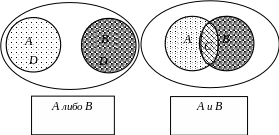
Рис. 1.

Операции объединения и пересечения множеств

Если определенному свойству элементов множества поставить в соответствие меру этого свойства, то получится множество величин. В математике исследуются числовые множества: R – действительных (вещественных) и С– комплексных (мнимых) чисел, I – иррациональных и Q – рациональных, N – натуральных и Z – целых чисел. Каждое из них обладает своими свойствами. Соотношения между числовыми множествами выглядят следующим образом:

В зависимости от обстоятельств или по условию, величины, составляющие множество, могут быть постоянными или переменными. Если в какой-либо науке в качестве элемента множества фигурирует событие, то для определения его мгновенного положения можно использовать пространственно-временную систему координат (x, y, z, t). В этом случае объединяются числовые множества координат и времени для построения математической модели меняющихся событий (процессов). Эти числовые множества часто являются упорядоченными по принципу «больше-меньше» или «раньше-позже», поэтому во многих случаях имеет смысл (вслед за Р.Декартом) использовать системы координатных осей x и y, как представителей упорядоченных числовых множеств.

Рис. 2. К определению функции как отношения между X и Y (а).

Упорядоченные числовые множества на осях координат

и вариант отношения между ними в виде графика функции (б)

Анализируя причины и следствия любых процессов, можно строить соответствующие математические модели, задав отношение между множествами, выражающими «причины» и «следствия». Например очевидно, что между количеством проданных товаров (множество Q) и доходом (множество R), полученным от реализации этих товаров, существует отношение, задаваемое с помощью цен (Р). При постоянной цене товара на рынке доход является функцией от количества проданного товара, а поэтому можно говорить о том, что отношение между множествами Q и R задается функцией.

Между множествами X и Y задано отношение в виде функции (рис.2а), если каждому элементу x_i из множества X найдется соответствующий ему элемент y_i из множества Y, такой, что появление x_i влечет за собой появление y_i. Формально, отношение записывается следующим образом:

y = f(x) и читается как «y есть функция от x».

Исторически сложилось, что переменную величину x называют аргументом (независимой переменной), а y – зависимой переменной (функцией), в то время как очевидно, что отношение характеризует закон f(x), связывающий переменные. Множество значений x, при которых переменные y являются действительными конечными величинами, называют областью определения функции, а множество соответствующих величин y образуют область значений функции. Говорят, что на множестве X задана функция f(x). Отношения между аргументом и функцией можно представить графически в декартовой системе координат (рис.2б), если на плоскости отметить точку (М) и опустить из нее перпендикуляры на оси координат. В этом случае, каждому значению аргумента с помощью точки М будет поставлено в соответствие определенное значение функции, а все отмеченные точки образуют множество отношений. На рис.2б это множество выглядит в виде жирной кривой линии (графика функции). Рассмотрим основные функции по мере их усложнения.