4.5.1 Доверительная значимость, доверительная вероятность, доверительный интервал, доверительный предел

Оценки, рассмотренные выше, являются точечными. В связи с этим возникает вопрос: можно ли по результатам точечной оценки одной лишь выборки судить о свойствах всей генеральной совокупности. На первый взгляд кажется, что нельзя. Из приведенного примера (таблица 49) видно, что средние не совпадают с генеральным средним. Однако каждый результат, полученный в отдельной выборке, можно рассматривать как случайную величину. Соответственно, при увеличении числа выборок, распределение точечных оценок будет принимать характер нормального распределения. Это значит, что в случае средних арифметических относительные отклонения выборочных средних от генерального среднего (т.е. характеристик непосредственно генеральной совокупности) распределяются также, как относительные отклонения нормально распределенных вариант от среднего арифметического вариационного ряда.

Отсюда, в частности, следует, что 68,3% всех выборочных средних находятся в пределах = М±т , где - предельная ошибка выборки, М- среднее выборочное, т- стандартное отклонение среднего значения (по аналогии со стандартным отклонением вариант от среднего вариационного ряда). Иными словами имеется вероятность 0,683 , что выборочное среднее отличается от генерального не более, чем на ±т. Вычисляется этот параметр в случае повторного отбора по формуле , где σ - среднеквадратическое отклонение выборки, n- число наблюдений в выборке (объем выборки), или , где D=σ² – дисперсия.

При определении ошибки выборочной доли (например: 0,25 или 0,47) используется формула . В случаях, когда доля выражена в % (например: 25% или 47%), . Указанным способом ошибки доли определяются, если число наблюдений достаточно велико. Необходимую величину выборки в этом случае можно найти из неравенства Рn>500, т.е. произведение доли (в %) на число наблюдений не должно быть меньше 500. Кроме того, чтобы использовать указанную формулу сами выборочные доли не должны намного отличаться от 0,5 (50%). В случае, когда доля меньше 0,2 (20%) или больше 0,8 (80%) , следует использовать другую методику.

Если выборка, объем которой известен (n), сформирована из генеральной совокупности бесповторным отбором, то в формулу вводится поправочный множитель, и она приобретает вид . Очевидно, что при большой генеральной совокупности, когда N —> °° , этот множитель стремится к единице.

В медико-биологической литературе параметр т принято называть «стандартная ошибка среднего» или «ошибка среднего», так как этот параметр характеризует ошибку утверждения (ошибку прогноза), что выборочное среднее равно генеральному среднему. Чем выше требование к доверительной вероятности этого вывода, тем шире должен быть обеспечивающий точность такого прогноза интервал, называемый «доверительный интервал».

Статистическая оценка, которая определяется двумя числами - концами интервала, называется интервальной оценкой.

Величина доверительного интервала задается вероятностью безошибочного прогноза, эту вероятность принято называть «до­верительная вероятность» или вероятностью безошибочного прогноза, а иногда надежностью. Величина доверительной вероятности может задаваться доверительным параметрическим коэффициентом t коэффициентом Стьюдента (псевдоним английского химика У.Госсета, 1908).

При достаточно большом числе наблюдений (n>30), значения доверительного коэффициента t и доверительной вероятности соотносятся следующим образом: Таблица 50

Соотношение статистических критериев достоверности выборочных характеристик

Доверительный критерий t	Доверительная вероятность (%)	Уровень значимости (Р)
1	68,3	0,32
2	95,5	0,05
3	99,7	0,01

При малых числах наблюдений значения коэффициента Стьюдента с учетом уровня доверительной вероятности можно установить по специальным таблицам.

Выбор того или иного уровня значимости или, соответственно, доверительной вероятности в общем является произвольным. В медико-биологических исследованиях допускается доверительная вероятность не менее 95,5%. В этом случае доверительный интервал для средних при достаточно большом числе наблюдений (n>30), равен ±2m. Предельная ошибка выборки  = М±2m. При доверительной вероятности 99,7% доверительный интервал составит ±3m, =М±Зm. В целом, чем больше доверительная вероятность, тем больше доверительный интервал и предельная ошибка.

Граничные точки доверительного интервала называются доверительными пределами.

Каждому значению доверительной вероятности соответствует свой уровень значимости (Р). Уровень значимости выражает вероятность нулевой гипотезы, т.е. вероятность того, что выборочная и генеральные средние не отличаются друг от друга. Иначе говоря, чем выше уровень значимости, тем меньше можно доверять утверждению, что различия существуют. Для доверительной вероятности 0,95 (95%), например, уровень значимости Р=1-0,95=0,05.

Таблица 51

Интервальная оценка среднего арифметического

М=25,2. m=3,1 n=50
Критерий Стьюдента 1	1	2	3
Доверительная вероятность	68,3%	95,5%	99,7%
Уровень значимости Р	0.32	0,05	0,01
Доверительный интервал t т	±3.1	±6.2	±9,3
Предельная ошибка выборки А	25,2±3,1	25.2±6,2	25,2±9,3
Доверительные пределы М+tт + М-tт	28,3/22,1	31.4/19.0	34,5/15,9

Если выборки небольшие по объему, то распределение вероятностей не следует точно нормальному закону распределения. В этом случае для определения величины доверительного коэффициента соответствующей определенному значению доверительной вероятности или уровню значимости пользуются специальными таблицами. Очевидно, что в реальных исследованиях желательно иметь как можно меньший доверительный интервал при достаточно высокой доверительной вероятности.

Таким образом, статистическая значимость выборочных характеристик представляет собой меру уверенности в их «истинности». Уровень значимости находится в убывающей зависимости от надежности результата. Более высокая статистическая значимость соответствует более низкому уровню доверия к найденной в выборке характеристике. Именно уровень значимости представляет собой вероятность ошибки, связанной с распространением наблюдаемого результата на всю генеральную совокупность.

Выбор порога уровня значимости, выше которого результаты отвергаются как статистически не подтвержденные, во многом произвольный. Как правило, окончательное решение обычно зависит от традиций и накопленного практического опыта в данной области исследований. Верхняя граница Р<0,05 статистической значимости содержит довольно большую вероятность ошибки (5%). Поэтому а тех случаях, когда требуется особая уверенность в достоверности полученных результатов, принимается значимость Р<0,01 или даже РО.001.

В практике медико-биологических исследований наиболее час­то используются следующие значения показателей значимости 0,1; 0,05; 0,01; 0,001. Традиционная интерпретация уровней значимости, принятая в этих исследованиях представлена в таблице 52.

Таблица 52

Интерпретация уровней значимости (Р)

Показатели значимости (Р)	Интерпретация
≥ 0.1	Данные согласуются с нулевой гипотезой Н0
≥0,05	Есть сомнения в истинности как нулевой Н0, так и альтернативной гипотез Н1.
<0.05	Нулевая гипотеза Н0 может быть отвергнута
≤0,01	Нулевая гипотеза (Н0 )может быть отвергнута Сильный довод
≤ 0,001	Нулевая гипотеза (Н0) почти наверняка не подтверждается. Очень сильный довод.

Из формулы стандартной ошибки среднего (m), от которой во многом зависит величина интервала, следует, что эта ошибка зависит как от числа наблюдений в выборке (n), так и от однородности выборки.

Интервальные оценки коэффициентов асимметрии, эксцесса и коэффициента вариации проводятся на основе стандартных ошибок этих коэффициентов.

Ошибка показателя асимметрии при очень малых объемах выборки может производиться по формуле . Ошибка показателя эксцесса . Ошибка коэффициента вариации .

В медико-биологических исследованиях объекты наблюдения, как правило, весьма вариабельны и не поддаются регулированию. Поэтому там, где это возможно, желательно брать выборки большего объема, что к сожалению в большинстве исследований весьма трудно или вообще невозможно. Поэтому значение выборочных статистических оценок в медико-биологических исследованиях не может быть определено с высокой точностью. Это в свою очередь делает бессмысленным точное измерение исходных данных. Поэтому при планировании исследований указанное обстоятельство необходимо обязательно учитывать, что позволит избежать ненужных материальных затрат (чем точнее измерения, тем они дороже) и неоправданных потерь времени при сборе данных.

Иногда при статистических расчетах необходимо вычислять сумму, разность, произведение и частное отделения средних величин. В этих ситуациях необходимо соответствующим образом оперировать и с ошибками средних.

Для определения суммарной ошибки суммы средних М1,+М2,+ ... +Мn можно использовать формулу: . Следует иметь в виду, что более точный результат суммарной ошибки получается при пересчете объединенного массива исходных данных (всех вариант), а указанной формулой следует пользоваться в случае невозможности такого перерасчета.

Формула ошибка разности средних арифметических М1,-М2-…- Мn вычисляется аналогично: .

Ошибка деления средних арифметических:

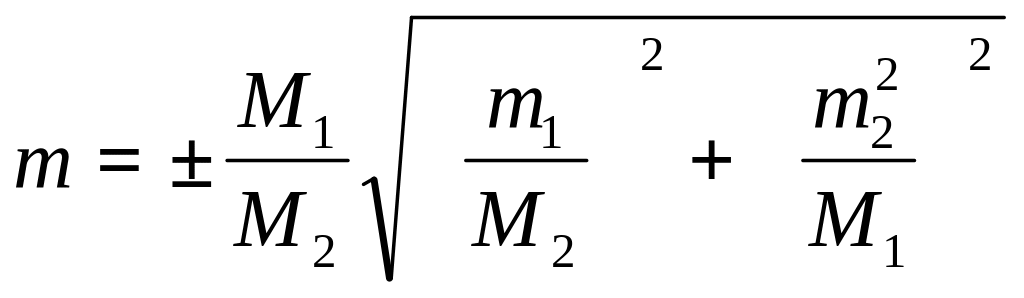
Ошибка произведения средних арифметических: