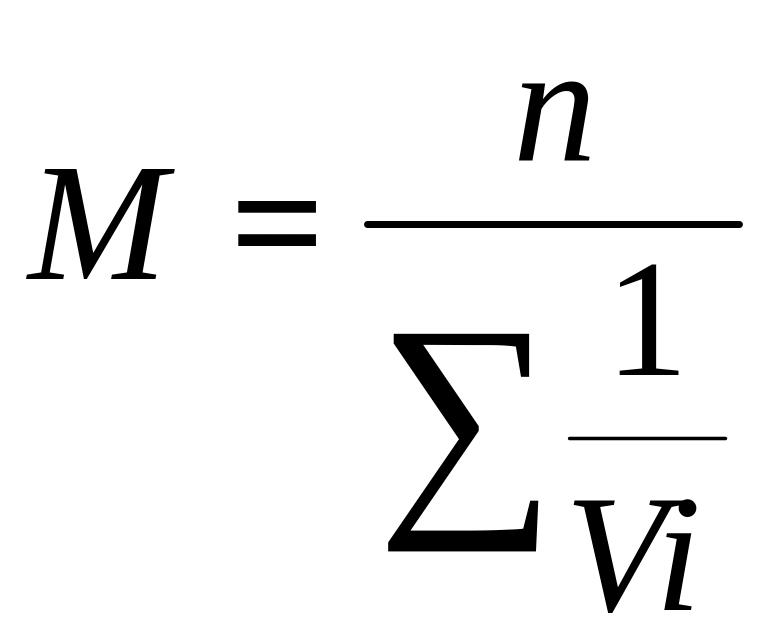4.2.1 Среднее арифметическое и другие степенные средние

Наиболее употребительной из средних величин является среднее арифметическое. Среднее арифметическое может обозначаться различным символом (М, А, и др.). В медицинской статистике чаще всего для его обозначения применяется символ М (от латинского Медиа - середина). Для простого среднего арифметического, которое вычисляется в простом, не сгруппированном вариационном ряду, используется формула: , или в более упрощенном виде , где n – число наблюдений, Vi – варианты (V1, V2, V3, V4..Vn). С арифметической точки зрения в основе вычислений лежат две простые операции: сложение всех вариант и деление полученной суммы на число наблюдений (Таблица 33).

Сгруппированный вариационный ряд иногда называют взвешенным рядом. Среднее арифметическое, рассчитанное в этом ряду, называют взвешенным средним , где n - число наблюдений, Vi- варианты, Pi - их частоты. Число наблюдений во взвешенном (дискретном) ряду определяется как сумма частот: . Соответственно, формулу для вычисления среднего можно представить в виде . При вычислении среднего взвешенного последовательно выполняют­ся следующие операции {Таблица 34):

1. Каждая варианта в таком ряду умножается на частоту ее встречаемости, как бы «взвешивается». (V₁*Р_1, V₂*Р_2, V₃*Р₃..V_nP_n). Чем больше частота варианты, тем больший «вес» она имеет при вычислении среднего. В том случае, когда среднее арифметическое определяется в интервальном ряду, т.е. варианты разбиты на группы, частоты перемножаются на серединные значения этих групп.

2. Полученные произведения суммируются:

3. Сумма произведений делится на число наблюдений, в результате чего получается среднее арифметическое.

Таблица 34

Способы вычисления среднего арифметического

Простое среднее		Взвешенное среднее			Способ моментов
V	P	V	P	V*P	V	P	d	P*d
15	1	15	1	15	15	1	-2	-2
16	1	16	3	48	16	3	-1	-3
17	1	17	5	85	A=17	5	0	0
18	1	18	4	72	18	4	1	4
19	1	19	2	38	19	2	2	4
ΣV=85	n=5		ΣP=15	ΣV*P=258		ΣP=15	ΣP*D=3
M=85/5=17		M=258/15=17.2			M=17+(3/15)*1=17.2

Упрощенным вариантом вычисления среднего арифметического является вычисление по способу моментов. Не вдаваясь в математическое обоснование способа моментов, можно выделить следующие этапы вычисления среднего этим способом (см. таблицу 33);

1. В ранжированном ряду распределения выбирается условное среднее А. За условное среднее можно принять любую варианту данного ряда. Для удобства вычисления лучше брать варианту ближе всего лежащую к центру ряда распределения и чаще всего встречающуюся (с наибольшей частотой Р).

2. Выставляются условные отклонения d. Их абсолютные значения последовательно увеличивают на единицу, начиная от 0, который соответствует варианте, принятой за условное среднее. Знак минус обозначает уменьшение вариант от условного среднего. Плюс - соответственное увеличение вариант.

3. Произведения условных отклонений на соответствующие им частоты (Рd) суммируются с учетом отрицательных знаков.

4. Для того, чтобы определить среднее арифметическое, полученная сумма делится на число наблюдений

Частное от этого деления умножается на величину интервала вариационного ряда , и к результату перемножения прибавляется условное среднее .

Нетрудно заметить, что вариационные ряды представляют собой арифметические прогрессии. В этих прогрессиях отдельные числовые значения или группы числовых значений признака располагаются строго упорядочено и с определенным интервалом. Вместе с тем, иногда встречается ситуация, когда все значения какого либо признака разбиты на несколько неравных по численности групп. В этом случае среднее арифметическое вычисляют, рассматривая каждую группу как самостоятельную совокупность. В каждой из этих групп сначала вычисляется своё среднее (групповое среднее). Затем на основе групповых данных определяют общее среднее, учитывая число наблюдений в каждой группе

Таблица 35

Пример вычисления общего среднего арифметического

Группа (J)	Первая		Вторая
Значение признака (V)	1	6	1	5
Частота (Р)	10	15	20	30
Число наблюдений (лЛ	10+15=25		20+30=50
Групповые средние М/
Общее среднее Мобщ

Таким образом: общее среднее равно среднему арифметическому групповых средних, взвешенных по объемам групп.

В клинической и лабораторной практике нередко возникает задача получить смесь каких либо компонентов с определенными свойствами. Например: Какая крепость спирта будет у смеси, состоящей из 10 литров 40%, 30 литров 70% и 50 литров 96% спирта?

Принцип решения этой и ей подобных задач состоит в применении суммирования взвешенных величин. Исходные данные в виде вариационного ряда будут выглядеть так (Таблица 36):

Таблица 36

Варианта (крепость спирта)	Вес (кг)
40	10
70	30
96	50

Вычисление среднего арифметического ряда и будет ответом на поставленную задачу. М=(40*10+70*30+96*50)/(10+30+50)=81,1. Путем несложного алгебраического преобразования можно решать и обратные задачи: сколько и какой крепости спирта надо добавить, чтобы получить необходимую концентрацию в заданном количестве. Однако, учитывая слабую подготовку медицинских работников в математике, можно предложить использование таблицы Ехсеl.

Расчет среднего арифметического с помощью современных статистических программ, установленных на компьютерах, в принципе, не требует построения рядов распределения. Однако когда вычисления производятся на основе рядов, варианты в которых - крупные числа, а также при большом объеме наблюдений, приемы упрощенного вычисления средних могут оказаться более быстрыми и более точными за счет сокращения ошибок, неизбежно возникающих при вводе в компьютер больших числовых массивов.

Например: требуется определить средний вес новорожденных детей. Варианты наблюдений - вес детей - представлены четырехзначными числами. Объем наблюдений также достаточно велик - 2500 детей. (Таблица 37). Если просто вводить в компьютер весь этот числовой массив или следовать обычному порядку вычислений среднего взвешенного, то придется оперировать большим количеством громоздких величин. Так, для получения среднего взвешенного, частоты Р необходимо перемножить на соответствующие им варианты V (вес в граммах) 100*3350,150*3400,175*3450 и т.д. Затем суммировать эти произведения и разделить на сумму частот (число наблюдений) 9046250/2500=3618,5.

При упрощенном вычислении проводить громоздких операций не требуется, поскольку вместо частот используются частости вариант. Т.е. промежуточные данные из столбика III (Таблица 37), заменяются другими, более простыми числами. Последовательность операций при вычислении среднего арифметического упрощенным способом выглядит следующим образом:

1. Определяем частости вариант в ряду распределения. Вычислить эти частости достаточно просто. Частоту конкретной варианты делим на общее число наблюдений: 100/2500=0,04150/2500=0,06 и т.д.

2. Затем находим условные отклонения от условного среднего (А). За условное среднее можно принять любую варианту. Лучше брать ту, которая находится ближе к середине ряда и чаще всего встречается (с наибольшей частотой). В нашем примере это варианта 3600 грамм. Выставляем условные отклонения (D), последовательно увеличивая их значения на единицу начиная от 0, который соответствует варианте принятой за условное среднее, до самой большой (со знаком плюс) и самой малой (со знаком минус).

3. После этого находим произведения частостей на условные отклонения (О): 0,04*(-5)=-0,20; 0,06*(-4)=Ч),24 и т.д.

4. Для получения искомого среднего арифметического эти произведения суммируются: 0,37 . После чего умножаются на величину интервала: 50*0,37 (в нашем примере интервал h= 50 грамм), и к этой сумме прибавляется условное среднее (в данном примере 3600 грамм): /^=50*0,37+3600=3618,5.

Таблица 37

Вычисление среднего арифметического упрощенным способом

Вес в граммах V	Число детей Р	VР	Частости ω	Условные отклонения D	ω D
I	II	III	IV	V	IV*V
3350	100	335000	0,04	-5	-0,20
3400	150	510000	0,06	-4	-0.24
3450	175	603750	0,07	-3	-0,21
3500	250	875000	0.10	-2	-0.20
3550	275	976250	0,11	-1	-0,11
А=3600	300	1080000	0,12	0	0
3650	375	1368750	0,15	1	0,15
3700	275	1017500	0,11	2	0,22
3750	225	843750	0.09	3	0,27
3800	200	760000	0,08	4	0,32
3850	125	481250	0,05	5	0,25
3900	50	195000	0,02	6	0,12
Всего	2500	9046250	1.00	-	0.37

В итоге, несмотря на кажущуюся сложность расчетов, для нахождения среднего арифметического громоздких вычислений не понадобилось.

Помимо среднего арифметического для характеристики центра (середины) распределения используются и другие параметры (средние величины). К ним, в частности, относятся среднее геометрическое, среднее гармоническое и среднее квадратическое. В математической статистике эти средние, как и среднее арифметическое, относят в группу так называемых степенных средних. Они имеют единое математическое выражение, отличающееся только коэффициентом к, который является коэффициентом статистической размерности признака. Разница между этими средними тем больше, чем больше вариабельность признака в статистическом ряду. При небольшой вариабельности разница между этими средними практически незаметна.

Таблица 38

Виды степенных средних величин

Алгебраическое выражение	Степенные средние
	Общая формула степенных
	Арифметическое К=1
	Гармоническое К=-1
	Квадратическое К=2
	Геометрическое К=0

В приведенных формулах: к- показатель степени (коэффициент статистической размерности); п -число наблюдений; V- варианты (если варианты представлены с частотами, то в формулы вводится Р).

Среднее гармоническое - применяется, когда дело имеют с обратными величинами (коли-индексы), сложными абсолютными величинами (тонна-километр, килограммометр) и т.п. Использование в этих случаях среднего арифметического приводит к ошибочным результатам. Например: В одном из районов к врачу психиатру в течение года из каждых 100 мужчин обратился 1 человек. Среди женщин 1 обратившаяся приходилась на 25 человек. Необходимо определить, на сколько жителей, в среднем, приходился один обратившийся. Для простоты вычислений будем считать. что общее число мужчин и женщин одинаково. Среднее арифметическое двух показателей (для мужчин и женщин) (25+100)/2=62,5 будет неверным. Правильно в этом случае определять среднее из обратных величин, через среднее гармоническое.

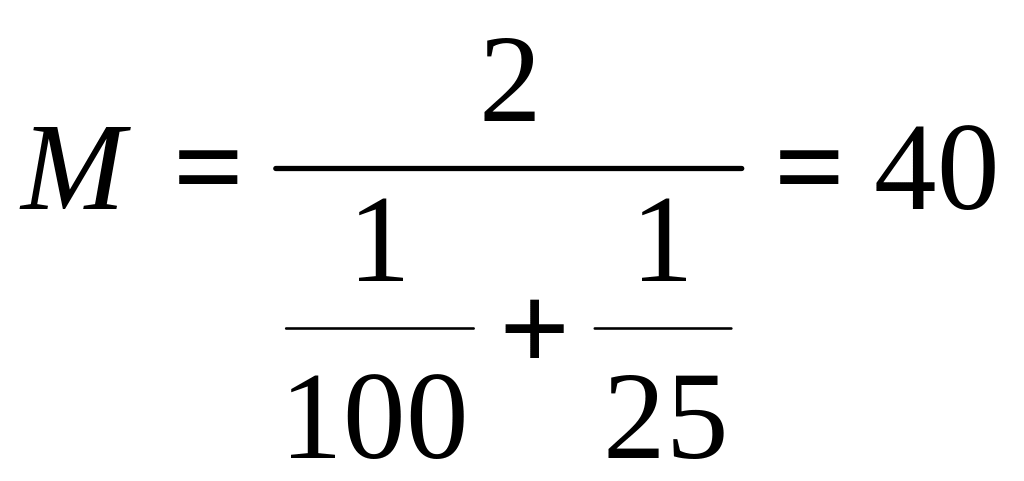
Т.о., из каждых 40 человек 1 был посетителем психиатра. Этот результат мог быть получен и через статистические коэффициенты (интенсивные показатели). Но в данной ситуации вычисление среднего гармонического значительно проще.

Среднее квадратическое (не путать со среднеквадратическим отклонением) - вычисляется, когда исходный ряд чисел представлен вариантами, отражающими значения площадей (площади ожогов, площади земельных участков и т.п.).

Среднее геометрическое - вычисляется в тех случаях, когда дело имеют с числовым рядом, отдельные значения в котором распределяются в геометрической профессии (резко отличаются друг от друга). Наиболее целесообразно вычисление этого показателя при определении среднего во временных рядах распределения. В целом, если при вычислении среднего арифметического подходят к рядам распределения с точки зрения разности между величинами, то при вычислении среднего геометрического подходят с точки зрения соотношения величин. Например: имеется два числа 4 и 16. Среднее арифметическое из них равняется 10, т.е. 10 больше 4 на столько же, на сколько 10 меньше 16. Среднее геометрическое из этих чисел равно 8. Число 8 в два раза меньше 16 и в два раза больше 4.

Чтобы лучше понять сущность среднего геометрического, рассмотрим пример спора некого Ноццолини и Галилея (XVII век). Лошадь, стоящая 100 крон, одним лицом оценивается в 10 крон, другим в 1000 крон. Какая из двух оценок менее ошибочна? Если рассматривать вопрос с арифметической точки зрения, на сколько ошибка велика, то получим в одном случае ошибку в 90 крон, а во втором - в 900 крон. Если оценивать, во сколько раз ошиблись покупатели, то получим одинаковый ответ для обоих - в 10 раз.*

* Пример взят из «Общей теории статистики». Ц.Б.Урланиса (1962г)

Кроме упомянутых степенных средних величин, в практике медико-биологических исследований используется среднее логарифмическое, если ряды распределения представлены логарифмами чисел (децибелы, pH и т.п.), среднее кубическое, если ряды распределения – объемы (объемы плазмы, крови, объемы эритроцитарной массы и т.п.). Таким образом, при вычислении среднего необходимо принимать во внимание фактический состав исходных данных.