Типовий приклад
Мета дослідження: Ознайомитись з основними складовими регресійного аналізу. Оволодіти навичками використання методу регресійного аналізу в дослідженнях систем міжнародних відносин/
Задача дослідження: провести змістовний аналіз досліджуваної системи за наступним планом:
1. Знайти лінійне регресійне рівняння для дискретної величини.
2. Знайти лінійне регресійне рівняння для неперервної величини.
Рішення задачі:
1. Дискретні величини:
За результатами проведеного аналітичного дослідження були отримані кількісні показники властивостей двох величин X та У при 30 спостереженнях. Дані спостережень наведені в таблиці:
Х |
0 |
5 |
10 |
20 |
nj |
У |
|||||
1 |
1 |
1 |
2 |
1 |
5 |
2 |
3 |
0 |
2 |
1 |
6 |
3 |
0 |
3 |
2 |
1 |
6 |
4 |
3 |
4 |
2 |
1 |
10 |
5 |
2 |
1 |
0 |
0 |
3 |
ni |
9 |
9 |
8 |
4 |
30 |
На основі даних спостережень розраховується:
математичне очікування величини Х: Mx=6.83
математичне очікування величини У: My=3.00
середньоквадратичне відхилення величини Х: Sx=6.39
середньоквадратичне відхилення величини У: Sy=1.26
коефіцієнт кореляції між величинами Х та У: Rxy =-0.25
регресійний коефіцієнт:
вільний член:
b = My - a Mx =3.00-(-0.056.83)=3.33
Відповідно регресійне рівняння має вигляд:
y=-0.05x+3.33
2.Неперервні величини:
За результатами проведеного аналітичного дослідження були отримані кількісні показники властивостей двох величин X та У за п’ять років (кількість спостережень n=5). Потрібно побудувати регресійне рівняння.
Дані спостережень наведені в таблиці:
№ |
Рік |
Xi |
Yi |
XiYi |
Xi2 |
1 |
2002 |
762,8 |
148,5 |
113275,8 |
581863,84 |
2 |
2004 |
495,9 |
123,4 |
61194,06 |
245916,81 |
3 |
2009 |
389,2 |
100,2 |
38997,84 |
151476,64 |
4 |
2003 |
385,1 |
80,1 |
30846,51 |
148302,01 |
5 |
2004 |
376,5 |
86 |
32379 |
141752,25 |
СУМА |
2409,5 |
538,2 |
276693,21 |
1269311,55 |
|
За даними таблиці:
регресійний коефіцієнт дорівнює
вільний член дорівнює
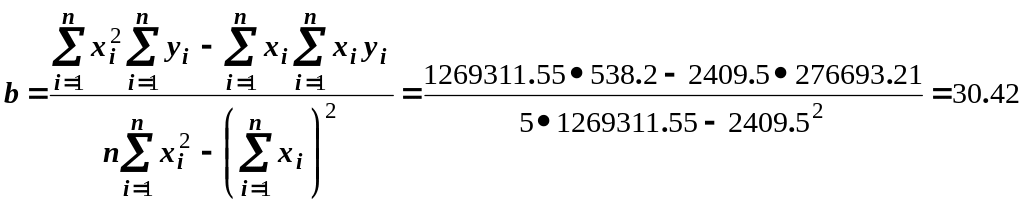
Відповідно регресійне рівняння має вигляд: y=0.16x+30.42
математичне очікування величини Х: Mx=481,9
математичне очікування величини У: My=107,64
середньоквадратичне відхилення величини Х: Sx=147,09
середньоквадратичне відхилення величини У: Sy=25,3
коефіцієнт кореляції між величинами Х та У: Rxy =0,93
регресійний коефіцієнт:
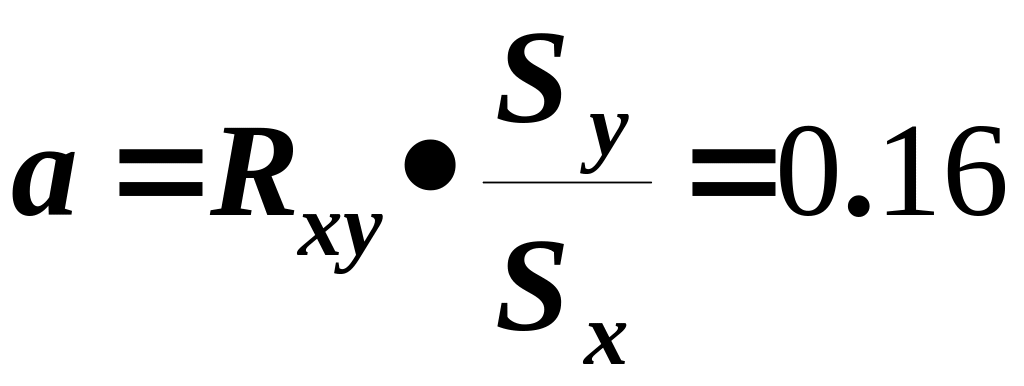
вільний член:
b = My - a Mx =30.42
Відповідно регресійне рівняння має той самий вигляд:
y=0.16x+30.42
Індивідуальне завдання
Використовуючи основні процедури та методи системного аналізу продовжити самостійне дослідження системи, що була обрана для дослідження (індивідуальне завдання Тема №1) за наступним планом:
1. Використовуючи методи регресійного аналізу, знайти регресійні рівняння для досліджуваних дискретних та непевних величин (за схемою типового прикладу).
2. Побудувати графіки отриманих функцій.
Поради до виконання індивідуального завдання
Якщо за результатами кореляційного аналізу виявився сильний зв’язок між величина, дані цих величин можна використати для побудови лінії регресії. Якщо зв’язок був слабким, чи взагалі не спостерігався, знайдіть інші величини. Пам'ятайте, що регресійний аналіз завжди починається з кореляційного.
В висновку, аналізуючи побудований графік, спрогнозуйте майбутні стани системи.
Теми для обговорення
1. Приклади зростаючих та спадаючих процесів в системі міжнародних відносин.
2. Методи визначення числа факторів в системі.
3. Аналітичні обмеження на використання регресійного аналізу.
Зразок тестових завдань
1. Якщо регресійне рівняння має вигляд у= - 3х+5, це означає
a) чим більше Х тим більше У
b) чим менше Х тим більше У
c) чим менше Х тим менше У