Задания для самостоятельной работы

Найти величину и направление напряжённости Н и индукции В магнитного поля в точке А. Конфигурации систем проводников для вариантов 1–20 представлены на рис. 4.6.1–4.6.20. Исходные данные вариантов указаны в табл. 2.

Рис. 4.6.1

Рис. 4.6.2

Рис. 4.6.3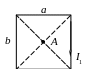

Рис. 4.6.4

Рис. 4.6.5

Рис. 4.6.6

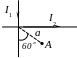
Рис. 4.6.7

Рис. 4.6.8

Рис. 4.6.9

Рис. 4.6.10

Рис. 4.6.11

Рис. 4.6.12

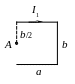
Рис. 4.6.13

Рис. 4.6.14

Рис. 4.6.15

Рис. 4.6.16

Рис. 4.6.18

Рис. 4.6.17

Рис. 4.6.19

Рис. 4.6.20

Таблица 2

№ вар.	I1, А	I2, А	I3, А	I4, А	а, м	b, м	с, м
1	4	–	–	–	0,6	–	–
2	2	–	–	–	0,2	–	–
3	4	–	–	–	0,3	–	–
4	6	3	–	–	0,1	0,2	–
5	2	3	–	–	0,8	–	–
6	6	3	–	–	0,4	–	–
7	4	6	–	–	0,2	0,6	–
8	4	2	–	–	0,2	0,4	–
9	2	3	–	–	0,3	0,6	–
10	4	–	–	–	0,4	–	–
11	3	–	–	–	0,5	–	–
12	4	8	–	–	0,4	0,3	0,5
13	4	4	2	2	0,8	0,4	–
14	3	–	–	–	0,4	0,4	–
15	4	6	–	–	0,6	–	–
16	2	4	–	–	0,2	0,4	–
17	5	2	–	–	0,7	0,3	–
18	4	4	–	–	0,3	0,3	–
19	2	3	–	–	0,4	0,4	–
20	4	–	–	–	0,4	0,4	–

5. Силовое действие магнитного поля на проводники с током Пример 5.1

Условие:

Рамка гальванометра длиной 4 см и шириной 1,5 см, содержащая 200 витков тонкой проволоки, находится в магнитном поле с индукцией 0,1 Тл параллельно линиям индукции. Какой вращающий момент действует на рамку, когда по виткам течёт ток силой 1 мА?

Дано: a = 4 см = 410–2 м b = 1,5 см = 1,510-2 м B = 0,1 Тл I = 1 мА= 110–3 А N = 200	Решение: Рис. 5.1
M = ?

На плоскость рамки действует сила Ампера, так как две грани параллельны линиям индукции, то сила Ампера на них не действует, из-за того, что угол между направлением вектора индукции магнитного поля и направлением тока в рамке равен нулю.

На две другие грани действует сила Ампера, которая создаёт вращающий момент. Вращающий момент можно найти по формуле

(5.1)

или в скалярном виде

, (5.2)

где B – магнитная индукция, p_m – магнитный момент контура, который можно найти по формуле

, (5.3)

S – площадь поверхности рамки , ограниченная контуром, N – число витков контура, I – сила тока.

Площадь поверхности, ограниченная контуром, находится по формуле

, (5.4)

где a и b – длина и ширина

Поставим в формулу (5.2) формулы (5.3) и (5.4), получим:

. (5.5)

Подставим числовые значения в формулу (5.5):

М = 0,04 0,0620010^–3 0,1 = 4,810^–4 Нм

Ответ: 4,810^–4 Нм.