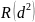5. Показательное (экспоненциальное) распределение

Функция распределения случайной величины, распределенной по показательному закону, имеет вид:

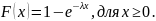
Используя обратное преобразование, получаем формулу для генерации последовательности экспоненциально распределенной случайной величины;

λ – среднее число каких – либо событий за единицу времени, х – промежуток времени между очередными событиями, Р – равномерно распределённая случайная величина в диапазоне от 0 до 1.

Распределение легко реализовать стандартными функциями Excel, поэтому в пакете Анализ данных соответствующий инструмент отсутствует.

Пример 6.1.5. Пусть есть магазин, в который время от времени заходят покупатели. При определённых допущениях время между появлениями двух последовательных покупателей будет случайной величиной с экспоненциальным распределением. Среднее время ожидания нового покупателя равно 1/λ. Сам параметр λ тогда может быть интерпретирован как среднее число покупателей за единицу времени. Пусть среднее число покупателей в час равняется 8, тогда случайный процесс, моделирующий приход покупателей в магазин можно получить с помощью формулы: =(-1/8)*ln(СЛЧИС()) . Ниже приведен фрагмент таблицы, моделирующий приход покупателей в магазин в течении 12 часов работы:

В ячейке В2 размещена формула =(-1/8)*ln(СЛЧИС()) , в ячейке С2 размещена формула =1/В2 . Таким образом в столбце В генерируется экспоненциально распределенное среднее время между очередными покупателями за час работы магазина, а столбце С среднее число покупателей за час работы магазина.

Контрольные задания по теме 6.1

Задание 6.1.1. Смоделируйте последовательность псевдослучайных чисел с дискретным законом распределения

Статистический анализ объемов реализации показал, что случайная величина Х, отражающая спрос на холодильники конкретной марки, характеризуется дискретным законом распределения. Суточные объемы продаж и их вероятности приведены ниже в таблице по вариантам:

Вариант	Параметры	Результаты частотного анализа по вариантам
1	Объем продаж, шт.	4	5	6	7	8	9
	Вероятность	0,05	0,1	0,34	0,3	0,17	0,04
2	Объем продаж, шт.	3	4	5	6
	Вероятность	0,12	0,65	0,18	0,05
3	Объем продаж, шт.	9	10	11	12	13
	Вероятность	0,08	0,25	0,37	0,2	0,1
4	Объем продаж, шт.	2	3	4	5
	Вероятность	0,15	0,35	0,4	0,1
5	Объем продаж, шт.	7	8	9	10	11
	Вероятность	0,11	0,3	0,35	0,15	0,09
6	Объем продаж, шт.	6	7	8	9
	Вероятность	0,1	0,35	0,35	0,2
7	Объем продаж, шт.	3	4	5	6	7	8
	Вероятность	0,04	0,12	0,3	0,26	0,2	0,08
8	Объем продаж, шт.	20	21	22	23	24
	Вероятность	0,1	0,3	0,35	0,15	0,1
9	Объем продаж, шт.	12	13	14	15	16	17
	Вероятность	0,06	0,26	0,3	0,2	0,12	0,06
10	Объем продаж, шт.	8	9	10	11	12
	Вероятность	0,05	0,25	0,35	0,3	0,05

Получите средствами MS Excel 15 реализаций случайной величины Х

Задание 6.1.2. Смоделируйте последовательность псевдослучайных чисел с нормальным законом распределения

Статистический анализ показал, что прибыль предприятия за месяц характеризуется средним значением m и стандартным отклонением σ. Для целей имитационного моделирования сгенерировать прогноз колебаний прибыли на 12 месяцев в предположении, что ее значение является нормально распределенным случайным процессом. Значения m и σ по вариантам приведены в таблице:

Вариант	Среднее значение прибыли, млн.руб.	Стандартное отклонение, млн.руб.
1	6,0	1,5
2	8,0	3,0
3	2,0	0,5
4	7,0	2,5
5	6,0	1,5
6	4,0	1,5
7	2,0	0,6
8	6,0	1,8
9	7,0	2,2
10	2,0	0,7

Задание 6.1.3. Смоделируйте последовательность псевдослучайных чисел с законом распределения Пуассона

Статистический анализ показал, что случайная величина Х, характеризующая число посетителей парикмахерской в течение рабочего дня подчиняется закону распределения Пуассона с параметром λ . Значения параметров  повариантно даны ниже в таблице:

Вариант	
1	29
2	60
3	59
4	35
5	40
6	49
7	22
8	52
9	22
10	49

Получите средствами MS Excel 15 реализаций случайной величины Х.

Задание 6.1.4. Смоделируйте последовательность псевдослучайных чисел с показательным законом распределения

Статистический анализ показал, что случайная величина Х, характеризующая длительность обслуживания клиента в парикмахерской следует показательному закону распределения с параметром . Значения параметров  повариантно даны ниже в таблице:

Вариант	
1	3
2	4
3	5
4	6
5	7
6	8
7	9
8	10
9	11
10	12

Получите средствами MS Excel 15 реализаций случайной величины Х.

С необходимым теоретическим материалом и примерами организации датчиков можно ознакомиться в литературе [2,стр.158-168].

Задание 6.2. Разработка имитационной модели хозяйственной операции

Методические указания к заданию 6.2.

В основе имитационных моделей лежит метод статистического моделирования (метод Монте-Карло). Этот метод позволяет воспроизводить на компьютере входные потоки исследуемого объекта, представляющие собой последовательности случайных чисел с заданными законами распределения ( датчики псевдослучайных чисел ). Моделируя процесс обработки входных последовательностей, мы можем рассчитать основные характеристики системы и оценить характер её реакции на воздействия внешней среды.

При использовании метода Монте-Карло для генерации случайных процессов с тем или иным законом распределения в качестве исходного используется случайный процесс с равномерным законом распределения.

В Excel равномерное распределение случайных чисел в диапазоне от 0 до 1 моделирует функция СЛЧИС().

Для моделирования равномерного распределения чисел в диапазоне от x до y используют формулу:

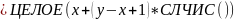
Равномерно распределенные последовательности случайных чисел используются для генерации последовательностей псевдослучайных чисел с другими законами распределения. В основе генерации лежит фундаментальное соотношение теории вероятности:

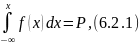
где Р – случайное число равномерно распределенное в интервале от 0 до1; x_i – случайное число с законом распределения, определяемым функцией плотности распределения f(x).

Таким образом, для получения последовательности чисел с заданным законом распределения, необходимо последнее уравнение разрешить относительно х, что не всегда возможно аналитически, а требует использования численных методов.

Например, для показательного закона распределения с плотностью распределения

решение уравнения (6.2.1) имеет вид:

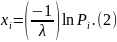
Для биноминального, гипергеометрического, Пуассона и нормального распределений в Excel имеются встроенные функции, позволяющие определить вероятность того, что случайная величина х может принимать значения либо равные, либо меньшие произвольной величины а, но не позволяют генерировать соответствующие последовательности случайных чисел с заданными параметрами распределения. Для этих целей в надстройку Excel «Анализ данных» включен инструмент «Генерация случайных чисел» для семи законов распределения: равномерного, нормального, Бернулли, биноминального, Пуассона, модельного, дискретного.

Приведем примеры типовых задач, информационные потоки которых адекватно описываются соответствующими законами распределения.

Биноминальное распределение используется при определении числа отказов при испытаниях определенного объема изделий; количества заказов, которые будут получены в результате определенного количества звонков в магазин; количества людей среди опрошенных, которые выразят желание купить данный товар и т.п. Например, необходимо определить вероятность того, что трое из пяти человек, зашедших в магазин, купят товар марки «А», причем известно, что 85% покупателей зашедших в магазин предпочитают товар именно этой марки.

Распределение Пуассона описывает число событий, происходящих в одинаковых промежутках времени при условии, что события происходят независимо друг от друга с постоянной интенсивностью λ: число отказавших изделий за определенный интервал; число требований выплаты страховых сумм в год; число обращений в ремонтную службу за сутки.

Нормальное распределение часто применяется в тех случаях, когда возможные значения лежат вокруг некоторого среднего значения: при стрельбе по мишени; измерении какого – либо параметра и т.п.

Экспоненциальное распределение используется для моделирования временных задержек между событиями, например времени, которое потребуется на доставку денежного перевода через автоматизированную банковскую систему.

Вопрос о согласованности теоретического и статистического распределений решается с помощью критериев согласия.

В дальнейшем при проверке проблемности гипотез можно использовать χ² - критерий Пирсона:

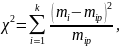
где к – количество разрядов при группировке;

i – порядковый номер разряда (интервала);

m_ip – расчетные (теоретические) частоты.

Для оценки соответствия экспериментального соответствия теоретическому можно воспользоваться либо таблицами, либо функцией Excel ХИ2РАСП(Х; ν), где х – неотрицательное число, для которого требуется вычислить распределение, а ν = k – s – 1 число степеней свободы (s – число параметров функции распределения).

Пример 6.2.1. С помощью электронной таблицы проведем имитацию работы мастерской, в которой работают два мастера. Когда рабочий заходит в мастерскую, когда мастера заняты выполнением ранее поступивших заказов, то рабочий уходит. Статистические данные показывают, что в среднем в час обращаются в мастерскую 18 рабочих. А среднее время, которое затрачивает мастер на заточку или ремонт инструмента, равно 10 мин. ( 1/6 часа ).

Оценить вероятность отказа в обслуживании в этой двухканальной СМО с отказами в предположении, что входящий поток рабочих – это простейший поток ( λ = 18 ), а время их обслуживания подчиняется экспоненциальному закону распределения ( µ = 6 ).

Решение. Имитационный эксперимент проведем в табличном процессоре Excel.

Моделирующий алгоритм приведен в таблице 6.2.1.

В клетках D1 и G1размещены параметры распределений потока заявок на обслуживание λ и среднего времени обработки заявок µ.

Строка 2 содержит информацию о количестве испытаний N, а в строке 3 располагаются непосредственно номера поступающих на обслуживание заявок.

В строке 4 генерируется последовательность равномерно распределенных случайных чисел в диапазоне от 0 до 1 с использованием функции =СЛЧИС() .

В строке 5 рассчитываются значение интервала между заявками по формуле (2) и соответствующего показательному закону распределения. Для этого в ячейку С5 помещается формула: =(-1/$D$1)*LN(C4) и копируется в остальные клетки строки.

В строке 6 рассчитывается время поступления заявок ( в минутах ) суммированием времени поступления предыдущей заявки и величиной интервала между заявками (строка 5 ). В ячейке С6 время поступления принимается равным 0, поэтому время поступления первой заявки равно интервалу (ячейка С5) и, соответственно, расчетная формула: =C5*60. В ячейке D6 расчетная формула имеет вид: =D5*60+C6 и далее копируется в остальные ячейки строки.

В строках 7 – 9 моделируется процесс обслуживания заявок первым мастером, в строках 10 – 12 моделируется процесс обслуживания заявок вторым мастером. В модели для упрощения формул приняты следующие допущения: 1) первая заявка обслуживается первым мастером; 2) если очередная заявка поступает, когда оба мастера свободны, то она поступает на обслуживание к первому мастеру.

В строке 7 моделируется время обслуживания заявки первым мастером в соответствие с формулой (2). В ячейке С7 размещена формула =60*(-1/$G$1)*LN(СЛЧИС()), формирующая время обслуживания первой заявки. В ячейку С8 заносится номер обслуживаемой заявки, а в ячейке С9 рассчитывается время окончания обслуживания заявки первым мастером. Далее расчет времени обслуживания в строке 7 производится только в том случае, если время поступления следующей заявки больше или равно времени окончания обслуживания заявки первым мастером. Одновременно в ячейке строки 8 обновляется номер обслуживаемой заявки и пересчитывается время окончания обслуживания очередной заявки. Если заявка поступила в момент, когда первый мастер занят, то она игнорируется и в ячейке строки 7 устанавливается 0, что является индикатором занятости первого канала. Ниже приведены формулы для пересчета ячеек строк 7, 8, и 9 на примере столбца D ( 2 – я заявка ):

D7: =ЕСЛИ(C9<D6;60*(-1/$G$1)*LN(СЛЧИС());0)

D8: =ЕСЛИ(D7>0;D3;C8)

D9: =ЕСЛИ(D8=C8;C9;D6+D7)

Эти формулы копируются в остальные ячейки соответствующих строк.

Таблица 6.2.1. Имитация двухканальной СМО с отказами

	A		B		C			D			E			F			G			H			I			J			K			L			M			N			O			P			Q
1	Параметры системы				λ =			18						µ =			6
2	Число испытаний N = 15
3	Требования: i = 1,2,…, N				1		2			3			4			5			6			7			8			9			10			11			12			13			14			15
4	Случ. числа P в диапазоне (0;1)				0,55		0,05			0,52			0,29			0,96			0,38			0,35			0,19			0,64			0,37			0,65			0,51			0,83			0,4			0,53
5	Время между заявками, час.				0,033		0,166			0,036			0,069			0,002			0,054			0,058			0,092			0,025			0,055			0,024			0,037			0,010			0,051			0,035
6	Время поступления заявок, мин				2,0		12,0			14,2			18,3			18,4			21,6			25,1			30,7			32,2			35,5			36,9			39,2			39,8			42,8			45
7	1	Время обслуживания		11,93		0			7,78			0			0			0			20,82			0			0			0			0			0			0			0			0
8		Обслуживаемая заявка		1		1			3			3			3			3			7			7			7			7			7			7			7			7			7
9		Время оконч. обсл.		14		14			22			22			22			22			46			46			46			46			46			46			46			46			46
10	2	Время обслуживания				5,80			0			0,74			0			10,40			0			0			6,67			0			0			0,19			4,07			0			5,49
11		Обслуживаемая заявка				2			2			4			4			6			6			6			9			9			9			12			13			13			15
12		Время оконч. обсл.				17,8			17,8			19,0			19,0			32,0			32,0			32,0			38,8			38,8			38,8			39,4			43,9			43,9			50,4
13	Счетчик отказов				0		0			0			0			1			0			0			1			0			1			1			0			0			1			0
14	Статистическая оценка вероятности отказа в СМО при n = 15 равна (5/15) = 0,33

Формулы реализации процедуры обработки поступающих заявок вторым мастером ( строки 10, 11, 12 ) аналогичны только что рассмотренным с той лишь разницей, что в строке 10 анализируется занятость первого канала ( заявка принимается к обслуживанию в том случае, если первый канал занят ). Формулы для пересчета ячеек строк 10, 11 и 12 на примере столбца D приведены ниже:

D10: =ЕСЛИ(D7=0;ЕСЛИ(C12<D6;60*(-1/$G$1)*LN(СЛЧИС());0);0)

D11: =ЕСЛИ(D10>0;D3;C11)

D12: =ЕСЛИ(D11=C11;C12;D6+D10)

Эти формулы копируются в остальные ячейки соответствующих строк. В ячейки С10, С11 и С12 формулы не заносятся, так как первая заявка всегда обслуживается первым мастером.

Строка 13 индицирует ситуацию занятости обоих каналов (одновременно установлены нули в 7 и 10 строках). В этом случае в соответствующую ячейку строки 13 записывается 1, что является признаком отказа в обслуживании.

Вероятность отказа определяется отношением числа отказов к числу испытаний N. В рассматриваемом примере Р_откз = 5/15 = 0,333.

Для удобства отладки и работы с моделью можно включить режим ручного пересчета. Для этого необходимо нажать верхнюю левую кнопку (Кнопка Microsoft Office) , а затем щелкнуть Параметры Excel и выбрать вкладку формулы. В разделе Параметры вычислений установить переключатель вручную, нажать ОК. В этом режиме пересчет таблицы будет происходить только при нажатии на клавиатуре функциональной клавиши F9.

Контрольное задание 6.2 по вариантам

Разработать имитационную модель хозяйственной ситуации, описанной ниже. При моделировании предполагать, что поток требований на обслуживание и продолжительность обслуживания распределены по экспоненциальному (показательному) закону.

В бухгалтерии организации в определенные дни непосредственно с сотрудниками работают два бухгалтера. Если сотрудник заходит в бухгалтерию для оформления документов (доверенностей, авансовых отчетов и пр.), когда оба бухгалтера заняты обслуживанием ранее обратившихся работников, то он уходит из бухгалтерии, не ожидая обслуживания. Статистический анализ показал, что среднее число сотрудников, обращающихся в бухгалтерию в течение часа, равно ; среднее время, которое затрачивает бухгалтер на оформление документа, равно Т_ср мин. (значения  и Т_ср по вариантам даны ниже в таблице 6.2.2.).

Оценить вероятность отказа в обслуживании.

Таблица 6.2.2. Исходные данные по вариантам к заданию 6.2.

Вариант	Параметр 	Параметр Тср=1/μ
1	18	9
2	4	6
3	16	10
4	8	7
5	14	11
6	12	8
7	10	7
8	8	9
9	15	11
10	10	12

Задание по теме 7: Метод экспертных оценок

Методические указания к заданию по теме 7

Метод экспертных оценок представляет собой процедуру, позво­ляющую группе экспертов приходить к согласию¹.

Предпосылки использования экспертных методов, организация и проведение экспертизы

Для широкого круга неформализуемых управленческих задач экспертные процедуры являются эффективным, а в ряде случаев и единственным средством их решения.

Можно привести многочис­ленные примеры применения экспертных оценок для решения задач прогнозирования, планирования, оперативного управления и конт­роля . Так, многие реальные и эффективные прогно­зы не были основаны на формальных моделях, а являлись результа­том качественного прогнозирования.

Прогнозирование на качественном уровне (без построения фор­мальных моделей) может быть важным источником информации.

Один из наиболее известных методов качественного прогнозирова­ния -метод Дельфи. Этот метод решает проблему получения объ­единенного прогноза, составленного на основе заключения группы экспертов.

Сущность метода экспертных оценок заключается в проведении квалифицированными специалистами-экспертами интуитивно-логического анализа проблемы с количественной оценкой суждений и формальной обработкой результатов. Получаемое в результате об­работки обобщенное мнение экспертов принимается как решение про­блемы. Другими словами, требуется получить групповое объективное мнение на основе некоторой совокупности индивидуальных субъек­тивных мнений экспертов.

Могут использоваться различные формы проведения экспертизы:

• дискуссия; • «мозговой штурм»;

• анкетирование; • деловая игра и др.

• интервьюирование;

Иногда различные формы используются в комплексе.

Можно выделить два больших класса методов экспертных оценок:

• индивидуальные экспертные оценки;

• групповые экспертные оценки.

Последовательность формирования групповых экспертных оценок приведена в следующей ниже таблице:

1. Формирование цели экспертизы и вопросов экспертам

2. Формирование правил проведения опроса экспертов или характера их взаимоотношений

3. Выбор способа оценки компетентности экспертов 4. Формирование группы экспертов

5. Формирование правил обработки мнений экспертов

6. Проведение опроса и определение групповых оценок

7. Определение степени согласованности экспертов

В разных методиках этапы экспертизы, представленные отдель­ными блоками общей блок-схемы, реализуются по-разному. В зави­симости от характера взаимоотношений между экспертами во время проведения коллективной экспертизы методы коллективной эксперт­ной оценки делятся на два класса:

• открытая дискус­сия,

• опрос с помощью анкет.

Представителями открытой дискуссии являются методы комиссий и «мозговых штурмов». Различие этих методов заключается только в том, что при «мозговом штурме» этапы генерирования идей и их критическая оценка разделены во времени.

Открытая дискуссия имеет недостатки:

• она не исключает давления авторитетов, т.е. мнение большин­ства приспосабливается к мнению наиболее авторитетных

• для оценки обобщенного мнения всей группы экспертов и степени согласованности экспертов не используется математиче­ский аппарат.

Проведение опроса экспертов с помощью анкет устраняет недостат­ки методов открытой дискуссии. Анкетирование исключает непо­средственное общение между членами экспертной группы. Свои заключения по поставленным перед ними вопросам эксперты пред­ставляют анонимно.

Одним из наиболее эффективных методов анкетирования явля­ется метод Дельфи (по названию древнегреческого города Дельфы, чьи оракулы славились умением предсказывать будущее). В этом методе участвуют координатор (прогнозист) и группа экспер­тов. Ни один из экспертов не знает, кто еще находится в этой группе, поскольку все контакты проходят через координатора. Дельфийский метод иллюстрируется следующей таблицей:

1. Координатор запрашивает прогнозы

2. Координатор получает индивидуальные прогнозы от каждого эксперта

3. Координатор определяет: средний прогноз; 50%-й интервал для среднего прогноза

4. Координатор запрашивает объяснения экспертов, чей прогноз не попал в 50% й интервал

5. Координатор отправляет всем экспертам: • средний прогноз; • 50%-й интервал для среднего прогноза; • объяснения

6. Возврат к пункту 1 (обычно до трех проходов)

7. Окончательная оценка точечного и интервального прогнозов

8. Конец

Основными особенностями метода Дельфи являются:

• полный отказ от личных контактов экспертов и от коллек­тивных обсуждений;

• многотуровая процедура опроса экспертов;

• обеспечение экспертов информацией, включая и обмен ин­формацией между ними, после каждого тура опроса при сохране­нии анонимности оценок, аргументации и критики;

• обоснование ответов экспертов по запросу координатора. Дельфийская процедура является сходящейся, так как от тура

• к туру мнения экспертов сближаются и уменьшается межквартильный размах в оценках.

Метод Дельфи имеет ряд недостатков:

• уровень компетентности участников может оказаться недо­статочным;

• сохранение анонимности снижает надежность информации и ответственность участников опроса;

• возможно ложное согласие участников опроса из-за неод­нозначности толкования вопросов.

Несмотря на это, метод Дельфи - одна из наиболее перспектив­ных форм проведения экспертного оценивания.

Применение методов экспертных оценок при принятии решений

Укажем, как результаты проведенной экспертизы могут быть ис­пользованы для прогнозирования экономических показателей.

Полученные от экспертов результаты оценок располагают в по­рядке возрастания. В качестве среднего прогноза (точечного прогноза) принимают медиану полученного ряда.

При интервальном прогнозе в ка­честве нижней и верхней границ доверительного интервала принима­ют значения первого и третьего квартиля соответственно (при межквартильном размахе доверительная вероятность прогноза 50%).

Пример 7.1. Десять экспертов оценили прогнозные значения экономического показателя:
Эксперт	1	2	3	4	5	6	7	8			9		10
Прогноз	16,9	13,8	11,9	12,3	16f3	12,0	16,1	20,6			16,8		13,1

Требуется методом Дельфи найти точечный и интервальный прогнозы.

Решение. Расположив результаты оценок в порядке возрастания, полу­чим следующий ряд:

11,9

12,0

12,3

13,1

13,8

16,1

16,3

16,8

16,9

20,6

Медиана - это среднее, полученное путем выявления «центрального» значения в перечне данных, расположенных в ранжированном порядке (иначе говоря, медиана - это значение признака у средней единицы ранжированного ряда). В общем виде при наличии п значений медиана отвечает [(n + 1)/2]- му порядковому номеру .

В последовательности из 10 данных значений медиана будет отвечать

[(10+ 1)/2] = [5,5] - му порядковому номеру

(т.е. номеру, который находит­ся посередине между 5-м и 6-м Значениями).

Таким образом, медиана равна 13,8 +(16,1-13,8)/2 = 14,95.

Определим значения первого и третьего квартиля:

♦ нижний (первый) квартиль Q₁ - значение признака у единицы ранжированного ряда, делящей совокупность в соотношении (1/4:3/4)

([(n+ 1)/4]) -е порядковое значение):

Q₁ = 12,0 + 0,75(12,3 - 12,0) = 12,225;

♦ верхний (или третий) квартиль (Q ₃ - значение признака у едини­цы ранжированного ряда, делящей совокупность в соотношении 3/4 : 1/4

([3(n + 1)/4]-е порядковое значение):

Q ₃ = 16,8 + 0,25(16,9-16,8) = 16,825.

Межквартильный размах Q ₃ - Q₁ включает 50% центральных значений.

Второй квартиль Q₂ есть не что иное, как медиана. При этом Q₂ = 14,95 и межквартильный размах Q ₃ - Q₁= 4,6. ♦

Интервальный и точечный прогнозы при анкетном опросе экспер­тов можно также получить методом статистической обработки резуль­татов экспертных оценок.

При статистической обработке результатов экспертных оценок В_i (значение прогнозируемой величины, данное i-м экспертом, i =1,2,..., п) в качестве точечной оценки принимает среднее значе­ние прогнозируемой величины:

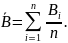
Далее определяются дисперсия D и оценка j для доверительно­го интервала:

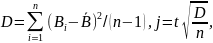
где t - коэффициенте Стьюдента для заданного уровня доверительной вероятности р и числа степеней свободы n - 2.

Доверительные границы для значения прогнозируемой величины

вычисляются по формуле:

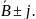
Пример 7.2. Десять экспертов оценили прогнозные значения эконо­мического показателя :

Эксперт	1	2	3	4	5	6	7	8	9	10
Прогноз	21,3	19,2	17,9	18,2	20,9	18,0	20,7	23,7	21,2	18,8

Методом статистической обработки ре­зультатов экспертизы найти точечный и интервальный прогнозы (р = 60%).

Решение. Сумма экспертных оценок составляет 199,9. В качестве точечной оценки принимают среднее значение прогнозируемой величины: 199,9/10 =19,99.

Для нахождения дисперсии D и оценки J для доверительного интер­вала используются функции Excel: (D = ДИСП(массив B_i) = 3.54) и (t = СТЬЮДРАСП0БР(0,4; 8) = 0,88).

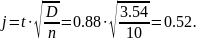
Верхняя граница доверителыюго интервала В + j = 19,99 + 0,52 = 20,51;

нижняя граница В - j = 19,99 - 0,52 = 19,47.

Достоверность оценок

Одной из наиболее актуальных проблем в области коллективной экспертной оценки при анкетной форме проведения экспертизы является повышение достоверности групповой оценки.

Эта проблема решается по двум направлениям:

1) проведение экспертизы в виде последовательности туров с вве­дением обратной связи, действующей после каждого тура. Под обратной связью понимается ознакомление экспертов с результатами каждого тура перед началом следующего;

2) учет степени компетентности участвующих в экспертизе экспертов. Компетентность экспертов может оцениваться как до проведения опроса, так и в ходе обработки полученных результатов. Эти вопросы рассматриваются, например, в учебнике .

Количественным выражением компетентности является вес, при­писываемый оценке эксперта, который учитывается при формирова­нии групповых опенок. Вес выражается в баллах некоторой шкалы. Чаше других принимается десятибалльная шкала оценок компетент­ности.

Различают следующие способы оценки компетентности экспертов:

• объективные - их можно подразделить на документальные и экспериментальные;

• субъективные - их можно подразделить на взаимооценочные и самооценочные.

При первом способе уровень компетентности экспертов определяется на основании характеристик, данных им другими участниками экспертизы.

Наиболее простым с точки зрения получения исходных данных является самооценочный способ определения компетентности экс­пертов. Этот способ не требует предварительной обработки каких-то данных для получения веса оценки эксперта. Сам эксперт определяет вес своей оценки по некоторому вопросу, пользуясь оценочной шка­лой, представляемой ему лицом, принимающим решение.

Как элементы совокупности соотносятся друг с другом по степе­ни важности, можно установить с помощью приема ранжирования. Ранжирование в общем случае представляет собой упорядочение по определенному признаку некоторой совокупности элементов. Такая упорядоченная цепочка элементов, составленная одним экс­пертом, называется ранжировкой. Каждый элемент, согласно месту, занимаемому им в ранжировке, получает свой порядковый номер или ранг.

При коллективном способе экспертной оценки результаты экспертизы можно считать достоверными лишь в случае, если будет достигнута достаточная степень согласия между участвующими в экс­пертизе экспертами. Поэтому необходимо выбрать меру, с помощью которой мы имели бы возможность измерять степень согласия между экспертами, а также оценивать приемлемость степени согласия.

Мерой близости ранжировок двух экспертов может служить коэффициент ранговой корреляции. В зависимости от способа исчисления связи между парами рангов в ранжировках экспертов коэффициент ранговой корреляции может быть посчитан по Кендаллу или по Спирмену.

При практических расчетах корреляционной зависимости ран­жировок предпочтительнее использовать удобную для расчетов фор­мулу коэффициента ранговой корреляции Спирмена :

где т - количество ранжируемых элементов; r_j1, r_j2 -ранг, полученный j-м элементом соответственно от первого и второго эксперта.

Значение коэффициента ρ может изменяться в пределах от -1 до +1:

• если ρ = 1, мнения экспертов относительно важности эле­ментов полностью совпадают;

• если ρ = -1, мнения экспертов полностью противоположны.

Пример 7.3. Два эксперта провели ранжирование шести экономических

признаков (табл. 7.1.).

Таблица 7.1..Результаты ранжирования

Эксперт	Ранг элемента
	Х1	Х2	Х3	Х4	Х5	Х6
Первый	1	2	3	4	5	6
Второй	2	3	1	4	6	5
d	-1	-1	2	0	-1	1
d2	1	1	4	0	1	I
	8

Рассчитаем коэффициент ранговой корреляции Спирмена:

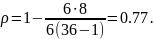
Таким образом, существует достаточно сильная положительная корре­ляция между ранжировками двух экспертов.

Для оценки степени согласованности мнений N экспертов используются специальные показатели, называемые коэффициентами конкордации (согласованности).

Предположим, что каждый эксперт ранжирует (упорядочивает) т элементов по убыванию их важности.

Первый член ранжировки получает 1-й ранг, последний- ранг, равный m (прямое ранжирование).

Наиболее известным является коэффициент конкордации Кендалла:

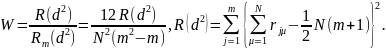
Коэффициент конкордации Кендалла меняется в пределах от 0 (в случае наименьшей согласованности мнений нескольких экспер­тов) до 1 (в случае абсолютной согласованности).

Величина N(m-1)W имеет распределение χ² с ν = m - 1 степенями свободы. Для признания значимости коэффициента кон­кордации необходимо и достаточно, чтобы найденное N(m - 1) W было больше табличного χ², определяемого числом степеней сво­боды и уровнем значимости α (вероятностью ошибки).

Таким образом, задавшись уровнем значимости и зная число сте­пеней свободы, можно получить в Excel с помощью функции = ХИ2ОБР табличное значение χ² и оценить значимость вычисленного по фор­муле коэффициента конкордации W. Чаще всего в подобных расчетах уровень значимости задается равным 0,05 или 0,01.

♦ Пример 7.4. Десять экспертов ранжировали по значимости следующие четыре показателя, характеризующие эффективность инвестиционных про­ектов:

Х₁— объем инвестиций;

Х₂ — срок окупаемости;

X3 — чистый дисконтированный доход;

Х₄ — рентабельность инвестиций (табл. 3.2). Определим коэффициент конкордации при m=4, N = 10:

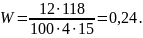
Получим расчетное значение χ²:

χ² = 103 0,24 = 7,2.

При уровне значимости α = 0,03 для ν = m - 1 = 3 степеней свободы находим табличное значение χ² с помощью функции =ХИ20БР (Мастер функций Excel/категория Статистические): χ²_табл = 7,8 .

Так как χ² < χ²_табл , то степень согласованности мнений экспертов W = 0,24 не только мала, но и не значима.

Таблица 7.2. Результаты ранжирования

Эксперт Э	Ранг rj показателя Xj
	X1	X2	X3	X4
Э1	4	2	1	3
Э2	3	1	2	4
Э3	1	2	3	4
Э4	3	1	2	4
Э5	3	2	4	1
Э6	3	4	1	2
Э7	3	1	2	4
Э8	2	1	3	4
Э9	2	4	1	3
Э10	3	2	1	4
Σ rj	27	20	20	33
dj	2	-5	-5	8
dj2	4	25	25	64
R(d2)	118

К обобщению мнений экспертов можно приступать лишь при достаточно высокой и статистически значимой согласованности мнений членов экспертной группы. II противном случае требуется дополнительная работа, в частности по выделению подгрупп экспертов с близкими мнениями.

Чем более согласованными являются ответы экспертов, тем надежнее их групповая оценка или суммарная ранжировка.

Один из подходов к обобщению мнений экспертов состоит в том, чтобы групповой считать ранжировку , наиболее тесно коррелирован­ную с N обрабатываемыми ранжировками.

Другой подход в рассматриваемой задаче состоит в том, чтобы групповую ранжировку искать как медиану индивидуальных.

Значительно шире на практике используется метод «сумм рангов» . Данный метод заключается в суммировании рангов по элемен­там, выставленных каждым экспертом, и определении групповой (обобщенной) ранжировки на основе суммарных рангов.

В примере 7.4 (см. строку Σ r_j таблице) обобщенная груп­пировка может быть представлена (прямое ранжирование) сле­дующим образом:

(Х₂) = (Х₃) > (Х₁) > (X₄),

где знак « = » означает «одинаково, равномерно», а знак «>» надо понимать как «предпочтительнее, важнее».

Определение групповых ранжировок при использовании других способов выражения предпочтений экспертов также основано на осреднении соответствующих оценок (балльных, непосредственных числовых) и построении на основе средних результатов обобщенной ранжировки.

В результате обобщения объективных данных и информации, получаемой от экспертов, а также собственных предпочтений ЛПР выбирает наилучшую альтернативу.

Контрольные задания по теме 7

Во всех вариантах заданий сделать точечный и интервальный прогнозы оцениваемого показателя. Достоверность оценок не проверять.

Вариант 1. Десять экспертов оценили прогнозные значения объёма продаж акций "Газпрома" (в млн. р.). Данные оценки приведены в таблице

эксперт	1	2	3	4	5	6	7	8	9	10
прогноз	16,8	12,9	12,8	13,6	11,9	12	16,1	20	17,8	13,4

Методом Дельфи экспертных оценок найти точечный и интервальный прогнозы объёма продаж.

Вариант 2. Десять экспертов оценили прогнозные значения объёма продаж акций "Газпрома" (в млн. р.). Данные оценки приведены в таблице:

эксперт	1	2	3	4	5	6	7	8	9	10
прогноз	16,8	12,9	12,8	13,6	11,9	12	16,1	20	17,8	13,4

Методом статистической обработки результатов экспертных оценок найти точечный и интервальный прогнозы объёма продаж.

Вариант 3. Восемь экспертов оценили объём кредитования юридических лиц некоторого коммерческого банка в условиях инфляции. Оценки приведены в таблице:

эксперт	1	2	3	4	5	6	7	8
прогноз	10,1	13,6	8,8	9,6	11,7	12	14,6	12,4

Методом Дельфи найти точечный и интервальный прогнозы объёма кредитования.

Вариант 4. Восемь экспертов оценили объём кредитования юридических лиц некоторого коммерческого банка в условиях инфляции. Оценки приведены в таблице:

эксперт	1	2	3	4	5	6	7	8
прогноз	10,1	13,6	8,8	9,6	11,7	12	14,6	12,4

Методом статистической обработки результатов экспертных оценок найти точечный и интервальный прогнозы объёма кредитования.

Вариант 5. Двенадцать экспертов оценили перспективный объём продажи механических наручных часов (в тысячах штук). Данные приведены в таблице:

эксперт	1	2	3	4	5	6	7	8	9	10	11	12
прогноз	7,8	9,6	13,1	8,4	10,2	11,6	12,5	13,6	8	10	9,8	10,4

Методом Дельфи найти точечный и интервальный прогнозы объёма продаж часов.

Вариант 6. Двенадцать экспертов оценили перспективный объём продажи механических наручных часов (в тысячах штук). Данные приведены в таблице:

эксперт	1	2	3	4	5	6	7	8	9	10	11	12
прогноз	7,8	9,6	13,1	8,4	10,2	11,6	12,5	13,6	8	10	9,8	10,4

Методом статистической обработки результатов экспертных оценок найти точечный и интервальный прогнозы объёма продаж часов.

Вариант 7. Восемь экспертов Красногорского завода оценили объём спроса на стеклопакеты (в млн. рублей) на 2013 год. Результаты приведены в таблице:

эксперт	1	2	3	4	5	6	7	8
прогноз	6,8	9,1	8,3	7	7,4	6,6	8,3	8,7

Методом Дельфи найти точечный и интервальный прогнозы спроса на стеклопакеты.

Вариант 8. Восемь экспертов Красногорского завода оценили объём спроса на стеклопакеты (в млн. рублей) на 2013 год. Результаты приведены в таблице:

эксперт	1	2	3	4	5	6	7	8
прогноз	6,8	9,1	8,3	7	7,4	6,6	8,3	8,7

Методом статистической обработки результатов экспертных оценок найти точечный и интервальный прогнозы спроса на стеклопакеты.

Вариант 9. Девять экспертов оценили спрос на малолитражные автомобили в городе N (в тысячах штук). Результаты приведены в таблице:

эксперт	1	2	3	4	5	6	7	8	9
прогноз	2,8	5,6	3,2	4,8	4	5	2,5	3,7	3,9

Методом Дельфи найти точечный и интервальный прогнозы спроса на малолитражные автомобили.

Вариант 10. Девять экспертов оценили спрос на малолитражные автомобили в городе N (в тысячах штук). Результаты приведены в таблице:

эксперт	1	2	3	4	5	6	7	8	9
прогноз	2,8	5,6	3,2	4,8	4	5	2,5	3,7	3,9

Методом статистической обработки результатов экспертных оценок найти точечный и интервальный прогнозы спроса на малолитражные автомобили.

Литература

а) Основная литература

1. Федосеев В.В., Гармаш А.Н., Орлова И.В. Экономико-математические методы и прикладные модели: учебник для бакалавров. 3-е изд., перераб. и доп.- М.: Издательство Юрайт, 2012.

2. Гармаш А.Н., Орлова И.В. Математические методы в управлении: учебное пособие, - М.: Вузовский учебник, 2012.

3. Орлова И.В., Половников В.А. Экономико-математические методы и модели: компьютерное моделирование Учебное пособие. - М.: ВЗФЭИ, Вузовский учебник, 2012.

4. Орлова И.В. Экономико-математическое моделирование: Практическое пособие по решению задач. – 2-е изд., испр. и доп. - М.: Вузовский учебник: ИНФРА-М, 2012.

б) Дополнительная литература

5. Кремер Н.Ш. Исследование операций в экономике. 2-е изд., перераб. и доп.- М.: Издательство Юрайт, 2012.

6. Афанасьев М.Ю., Багриновский К.А., Матюшок В.М. Прикладные задачи исследования операций: Учеб. пособие – М.: ИНФРА-М, 2006.

7. Экономико-математические методы и модели. Задачник: учебно-прак. пособие/под ред. С.И. Макарова, С.А. Севастьяновой.-2-е изд.,перераб.-М.: КНОРУС, 2009.

8. Томас Р. Количественные методы анализа хозяйственной деятельности.- М.: ДИС, 1999. - 432 с.

9. Эддоус М., Стэнсфилд Р. Методы принятия решения. – М.: ЮНИТИ, 1997. -590 с.

10. Стрикалов А.И. . Экономико-математические методы и модели: пособие к решению задач.- Ростов н/Д: Феникс, 2008.- 348 с.

11. Мур Дж., Уэдерфорд Л. Экономическое моделирование в Microsoft Excel. – М.: Издательский дом «Вильямс», 2004.

Приложение

Образец титульного листа контрольной работы

Федеральное государственное образовательное

бюджетное учреждение высшего профессионального образования

«Вятский государственный университет»

Факультет экономики и менеджмента

Кафедра «Экономико-математические методы и аналитические информационные системы»

Методы оптимальных решений

Контрольная работа

Вариант __

Выполнил студент __________

факультет__________

группа__________

номер зачетной книжки__________

Руководитель ______________

Киров 2014

77