Практическая часть

Задания по теме 2. Линейное программирование (ЛП)

Методические указания по теме 2

Формальные модели задачи ЛП

Задача линейного программирования является разновидностью задачи математического программирования вида:

Найти

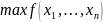
при условиях

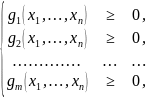
где функции f(x₁ , … , x_n), g_i(x₁ , … , x_n), i = 1 , … , m в общем случае нелинейны.

В том случае, если функции f(x₁ , … , x_n) и g_i(x₁ , … , x_n) линейны относительно х_j , то имеет место задача линейного программирования:

Найти

при ограничениях

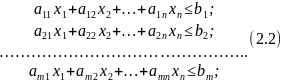
и

Где f(x₁ , … , x_n) – целевая функция или показатель эффективности решения; Х = x₁ , … , x_n исследуемые параметры моделируемой задачи; g_i(x₁ , … , x_n) – функции - ограничения, формирующие область решения. Условие (2.3) называют условиями неотрицательности.

Если все ограничения (2.2) задачи ЛП заданы в виде строгих равенств, то данная форма называется канонической.

Задача ЛП может быть записана в матричной форме:

Найти

При условии

где А – матрица из элементов a_ij системы ограничений (2.2) ; b = (b₁ , … , b_m) вектор - столбец из элементов правых частей ограничений; с^Т = (с₁ , … , с_n) – вектор – строка коэффициентов целевой функции.

Решение X^* называется оптимальным, если для него выполняется условие

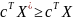
для всех Х, принадлежащих области допустимых решений, формируемой условиями (2.2).

Формализация задач ЛП

Ниже рассмотрены примеры построения формальных моделей типовых задач ЛП.

Пример 2.1. Задача оптимального использования ресурсов.

Предприятие имеет в своем распоряжении определенное количество ресурсов: рабочая сила, финансы, сырьё, оборудование, производственные площади и т.п.

Рассмотрим пример, когда предприятие ограничено ресурсами трех видов: рабочая сила, сырье и оборудование. Предприятие может выпускать гобелены четырех видов: «Пейзаж», «Закат», «Меланхолия», «Орнамент». Количество трех видов ресурсов ограничено суточными объемами: труд – 700 (чел./часов), оборудование – 280 (станко/часов), сырье – 300 (кг). Информация о нормах расхода каждого ресурса на один гобелен каждого вида, и доходах, получаемых от продажи единицы товара, приведена в таблице:

Ресурсы	Нормы расхода ресурсов на единицу изделия				Лимит ресурсов
	«Пейзаж»	«Закат»	«Меланхолия»	«Орнамент»
Труд	5	6	4	5	700
Оборудование	4	8	2	3	280
Сырьё	5	3	8	9	300
Цена (тыс.руб.)	3	2	3	5

Найти такой план производства продукции, который обеспечит максимальную суточную общую стоимость.

Обозначим через х₁, х₂, х₃, х₄ количество гобеленов каждого вида произведенных в течении рабочего дня. Тогда экономико – математическую можно представить в виде:

найти

при ограничениях на ресурсы

Пример 2.2. Задача о размещении средств.

Предприятие на планируемый год имеет собственных средств 80 млн. руб. Часть этих средств, но не менее 30 млн. руб. размешается в инвестиционных проектах. Эти активы являются неликвидными, так как не могут быть быстро конвертируемы в наличные средства в случае необходимости.

Часть средств инвестируется в ценные бумаги, которые можно легко реализовать без большого убытка. Финансовый менеджмент предприятия накладывает ограничение по ликвидности на уровне 25%, то есть ценные бумаги должны составлять не менее 25% от общей суммы размещенных средств.

Обозначим через х₁ – средства, размещенные в проектах, а через х₂ – средства, размещенные в ценных бумагах. Целью предприятия является получение максимальной прибыли от вложенных средств. Пусть средняя доходность по проектам составляет 10% годовых, а по ценным бумагам 18% годовых.

Теперь задачу определения оптимальной структуры инвестиционного портфеля можно сформулировать как задачу ЛП:

найти

при условиях

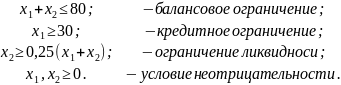
Пример 2.3. Задача составления рациона (задача о диете, задача о смесях).

Имеется два вида корма А и Б, содержащего питательные вещества (витамины, микроэлементы и т.п.) D₁, D₂ и D₃. Содержание числа единиц питательных веществ в 1 кг каждого вида корма и необходимый минимум и их необходимый минимум в суточном рационе, а также стоимость 1 кг корма приведены в таблице:

Питательное вещество	Число ед. питательного вещества в 1 кг. корма		Необходимый минимум
	А	Б
D1	3	1	9
D2	1	2	8
D3	1	6	12
Цена 1 кг, руб.	4	6

Обозначим через х₁ и х₂, количество кг кормов А и Б в суточный рацион. Тогда задача ЛП на минимизацию стоимости суточного рациона с удовлетворением требований по содержанию в рационе необходимого количества питательных веществ будет иметь вид:

найти

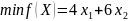
При ограничениях на ресурсы

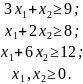
При наличии соответствующей информации в качестве критерия эффективности решения задачи можно рассматривать максимальные привес или удой.

Пример 2.4. Задача о раскрое материала.

Из поступающих на распил 195 бревен длиной 6 метров необходимо изготовить максимальное количество комплектов брусьев. Комплект должен состоять из 2-х брусьев длиной 1,2 м, одного бруса длиной 3 м и 3 бруса длиной 5 м (вариант комплектации условный).

В соответствии с условиями задачи можно сформировать четыре способа распила бревен:

1. 5 бревен длиной по 1.2 метра;

2. 2 бревна длиной по 1.2 метра и одно бревно длиной 3 метра ;

3. 2 бревна длиной 3 метра ;

4. 1 бревно длиной 5 метров.

Обозначим через Х число требуемых комплектов. Тогда условия задачи можно отобразить в виде следующей таблицы:

Способ распила	Число получаемых брусьев длиной в метрах
	1,2 метра	3 метра	5 метров
1 - способ	5 шт.	-	-
2 - способ	2 шт.	1 шт.	-
3 - способ	-	2 шт.	-
4 - способ	-	-	1 шт.
Условие комплектности	2	1	3

Теперь можно записать формальную модель рассмотренной задачи:

найти

при ограничениях

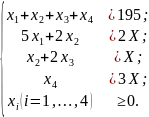
Решение задачи ЛП средствами MS Excel

Рассмотрим технологию решения на примере задачи оптимального использования ресурсов.

Пример 2.5. Исходные данные для иллюстрации метода возьмем из примера 2.1. Экономико-математическая модель задачи имеет вид:

найти

при ограничениях на ресурсы

В таблице Excel вычисляем значения целевой функции и функции левых частей ограничений, а затем решаем задачу с использованием пакета Поиск решения. Шаблон для решения задачи с введенными исходными данными приведен на рис. 2.1:

Рис. 2.1. Шаблон решения примера 2.1 с исходными данными.

Блок ячеек B3:E3 зарезервирован под искомые значения переменных Х. Переменным присвоены единичные значения, что можно рассматривать как начальную точку для поисковой процедуры. Кроме того, легко проверить безошибочность введенных формул: числа в столбце G равняются сумме чисел по строкам;

Блок ячеек B5:E5 содержит коэффициенты целевой функции (цены продаж);

Блок ячеек B8:E10 содержит коэффициенты матрицы ограничений (нормативы затрат ресурса на единицу изделия);

Блок ячеек I8:I10 содержит значения правых частей ограничений (лимит имеющихся в наличии ресурсов);

Формулы для расчета значения целевой функции (ЦФ) и значений левых частей ограничений приведены в нижеследующей таблице:

Адрес ячейки	Формула
G5	=СУММПРОИЗВ(B3:E3;B5:E5)
G8	=СУММПРОИЗВ(B3:E3;B8:E8)
G9	=СУММПРОИЗВ(B3:E3;B9:E9)
G10	=СУММПРОИЗВ(B3:E3;B10:E10)

В главном меню выбираем пункт Данные и нажимаем кнопку Поиск решения и заполняем открывшееся диалоговое окно (рис. 3.2.) и нажимаем кнопку Выполнить:

Рис. 2.2. Исходные данные для запуска процедуры численного решения задачи.

После завершения процедуры процессор сообщит, что решение найдено. Таблица шаблона с результатами решения примет следующий вид:

В ячейках B3:E3 мы видим оптимальные значения переменных:

В ячейке I5 число 181 означает максимальный объем выручки, соответствующий найденной оптимальной структуре выпуска продукции.

Двойственная задача линейного программирования

С каждой задачей ЛП тесно связана другая линейная задача, называемая двойственной. Решение одной из них может быть получено непосредственно из решения другой.

Рассмотрим модели исходной(прямой) и двойственной задач в общем виде.

Прямая задача (ПЗ):

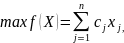
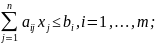
Двойственная задача (ДЗ):

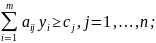
Переход от прямой задачи к двойственной осуществляется согласно следующим правилам:

1. Вводятся переменные y_i , число которых соответствует числу ограничений ПЗ;

2. Характер экстремума в ДЗ меняется на противоположный;

3. Знак неравенств в ДЗ меняется на противоположный;

4. Коэффициенты целевой функции c_j ПЗ становятся правыми частями ограничений ДЗ;

5. Правые части ограничений b_i ПЗ становятся коэффициентами целевой функции ДЗ;

6. Матрица А, составленная из коэффициентов a_ij при переменных ПЗ транспонируется в ДЗ;

7. Число ограничений в ДЗ равняется числу переменных в ПЗ.

Переменные двойственной задачи y_i называют объективно обусловленными оценками, или двойственными оценками, или «ценами» ресурсов, или теневыми ценами.

Теоремы двойственности

Теоремы устанавливают связь между оптимальными решениями прямой и двойственной задач.

1. Если X₀ и Y₀ допустимые решения прямой и двойственной задач, то

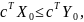
то есть значения целевой функции ПЗ никогда не превышают значения целевой функции ДЗ;

2. Если X₀ и Y₀ допустимые решения прямой и двойственной задач и если

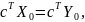
то X₀ и Y₀ оптимальные решения прямой и двойственной задач, то есть X₀ = X^* и Y₀ = Y*;

3. Для того, чтобы допустимые решения прямой и двойственной задач стали оптимальными, необходимо и достаточно, необходимо и достаточно, чтобы выполнялись следующие условия:

Смысл этих отношений состоит в следующем: если какое-либо неравенство выполняется как строгое (выражение в скобках равно нулю), то соответствующая ему переменная противоположной задачи равна нулю и наоборот.

Эти условия позволяют, зная оптимальное решение одной из задач, найти оптимальное решение другой задачи.

Рассмотрим построение двойственной задачи и её решение с использованием теорем двойственности на предыдущем примере.

Пример 2.6. Исходная задача о распределении ресурсов (прямая задача), рассмотренная в примере2.1.имеет вид:

найти

при ограничениях на ресурсы

Оптимальное решение прямой задачи:

В соответствии с правилами 1) – 7) двойственная задача имеет вид:

найти

при ограничениях

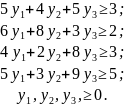
Подставим оптимальные значения переменных x_j^* в систему ограничений прямой задачи:

Так как первое неравенство выполняется как строгое, из условия (2.4) следует, что y₁^* = 0.

Так как х₁^* ≠ 0 и х₂^* ≠ 0, то из условия (2.5) следует, что первое и второе ограничения двойственной задачи должны быть равенствами. С учетом, что y₁^* = 0 имеем систему уравнений:

решая которую, находим y₂^* = 1/28 и y₃^* = 4/7. Таким образом, оптимальное решение двойственной задачи равно:

y₁^* = 0; y₂^* = 1/28 = 0,036 ; y₃^* = 4/7 = 0,571.

Подставим эти значения в целевую функцию двойственной задачи.

Значения целевых функций прямой и двойственной задач для оптимальных решений совпали, что удовлетворяет второй теореме двойственности.

Переменные y₂^* и y₃^* соответствуют ограничениям на сырьё и оборудование. Их оптимальные решения показывают, что каждая дополнительный кг сырья даст прирост прибыли на 1/28 тыс. руб., а каждый дополнительный станко/час обеспечит прирост прибыли на 4/7 тыс. руб.

Решение двойственной задачи в среде MS Excel

Технология решения двойственной задачи в среде MS Excel не отличается от рассмотренной выше технологии решения для прямой задачи, изменяется только форма и содержание шаблона. Поэтому ниже приводится только фрагмент таблицы с решением двойственной задачи.

В клетках B3: D3 таблицы мы видим оптимальные значения двойственных оценок, совпадающие с результатами, полученными с использованием теорем двойственности.

Постоптимизационный анализ

Программа Поиск решения дает возможность произвести анализ устойчивости найденного решения к вариациям, как значений коэффициентов целевой функции, так и правых частей ограничений прямой задачи.

Для этого необходимо повторно запустить программу Поиск решения для прямой задачи ЛП. После её выполнения появится следующее диалоговое окно Результат поиска решения (рис.2.3). Далее необходимо выбрать тип отчета Устойчивость. В низу таблицы появится новый рабочий лист Excel с именем Отчет по устойчивости (рис. 2.4).

В первых трех строках указаны реквизиты отчета .

Рис. 2.3. Диалоговое окно Результаты поиска решения

В таблице отчета Изменяемые ячейки содержатся следующая информация:

• Адреса ячеек, выделенные под переменные Х и наименование переменных (столбцы В и С);

• Оптимальные значения переменных (столбец D);

Рис. 2.4. Отчет по устойчивости

• Разность значений правых и левых частей ограничений двойственной задачи (столбец «Нормируемая стоимость»). По сути они характеризую «уровень технологичности» производства того или иного изделия. В нашем примере нетехнологичными оказались переменные Х3 и Х4 (гобелены «Меланхолия» и «орнамент») поэтому их объемы производства равны нулю;

• Коэффициенты целевой функции (столбец F);

• Нижний и верхний пределы изменения коэффициентов целевой функции, внутри которых сохраняется найденное решение (столбцы G и H). По сути, это допустимы диапазон цен на изделия Х, внутри которого структура оптимального решения не изменится. Например, независимо от того, увеличим мы цену изделия Х₁ на 0.3 (300 руб.) или уменьшим её на 0.1 (100 руб.), наиболее выгодные объемы выпуска продукции останутся прежними: Х₁^* = 56, Х₂^* = 7, Х₃^* = 0, Х₄^* = 0.

В таблице отчета Ограничения содержатся следующая информация:

• В ячейках В17:С19 располагаются адреса и имена ограничений задачи по ресурсам;

• В столбце D: «Результативное значение», приведены объемы фактически израсходованных ресурсов;

• В столбце «Теневая цена» расположены оптимальные значения переменных двойственной задачи. Мы видим, что ресурс «труд» используется не полностью, поэтому его теневая цена равна нулю;

• В столбце F размещаются значения правых частей ограничений прямой задачи, то есть предельные значения объемов ресурсов, которыми располагает предприятие;

• В ячейках В17:С19 располагаются допустимые пределы изменения Нижний и верхний пределы изменения запасов ресурсов. Эта информация важна с точки зрения принятия решения о дополнительном вовлечении ресурсов в производство с целью увеличения объемов выпуска продукции: привлечение дополнительных ресурсов или их сокращение приведет к изменению объемов производства и, соответственно, к увеличению или снижении прибыли. Поскольку целью задачи является увеличение прибыли, то вариант уменьшения лимита ресурса рассматривать нецелесообразно. Рассмотрим дополнительное привлечение ресурсов:

Ресурс «Труд». Его допустимое увеличение неограниченно. Однако делать это нецелесообразно, так как его теневая цена равна 0, поэтому дополнительное привлечение рабочей силы не приведет к росту прибыли.

Ресурс «Оборудование». Его допустимое увеличение равно 520 станко/часам. Каждый дополнительный станко/час даст прирост прибыли на 0,036 тыс. руб. (теневая цена). Увеличим лимит этого ресурса на 500 ед., тогда прирост прибыли составит ∆f = 0,036∙500 = 18 тыс. руб.

Ресурс «Сырьё». Его допустимое увеличение равно 50 кг. Каждый дополнительный кг даст прирост прибыли на 0,571 тыс. руб. (теневая цена). Увеличим лимит этого ресурса на 45 ед., тогда прирост прибыли составит ∆f = 0,571∙45 = 25,7 тыс. руб. ≈ 26 тыс. руб.

Посмотрим, как отразятся эти изменения на оптимальной структуре выпуска. Для этого скорректируем правые части ограничений в таблице (рис.2.1) и запустим программу поиск решения:

Из таблицы видно, что прибыль увеличилась на рассчитанные 44 тыс.руб. Изменились и объемы производства, однако структура выпуска сохранилась – изделия третьего и четвертого видов выпускать нецелесообразно.

Ниже приведено десять вариантов содержательной постановки задачи линейного программирования. В задании необходимо выполнить следующее:

1. Записать формальную задачу ЛП;

2. Решить задачу с помощью средств MS Excel (надстройка Поиск решения);

3. Составить двойственную задачу ЛП;

4. Решить двойственную задачу с использованием теорем двойственности;

5. Осуществить проверку правильности решения двойственной задачи с помощью средств MS Excel (надстройки Поиск решения).

6. Сделать содержательный анализ полученного решения, используя Отчет по устойчивости программы Поиск решения.

С графическим методом решения ЗЛП и примерами решения подобных задач можно ознакомиться в литературе /1, стр. 53-60/, технологией оптимизации в среде MS Excel – в /2, стр. 28-48/. Кроме того, полезно дополнительно привлечь литературу /3,4,11/.

Контрольные задания по теме 2

Вариант 1. Инвестор, располагающий суммой в 300 тыс. ден. ед., может вложить свой капитал в акции автомобильного концерна А и строительного предприятия В. Чтобы уменьшить риск, акций А должно быть приобретено по крайней мере в два раза больше, чем акций В, причем последних можно купить не более чем на 100 тыс. ден. ед. Дивиденды по акциям А составляют 8% в год, по акциям В – 10%. Какую максимальную прибыль можно получить в первый год?

Вариант 2. Совхоз для кормления животных использует два вида корма. В дневном рационе животного должно содержаться не менее 6 единиц питательного вещества А и не менее 12 единиц питательного вещества В. Какое количество корма надо расходовать ежедневно на одного животного, чтобы затраты были минимальными? Использовать данные таблицы:

Корма Питательные вещества	Количество питательных веществ в 1 кг корма
	1	2
А В	2 2	1 4
Цена 1 кг корма, т.руб.	0,2	0,3

Вариант 3. Некоторая фирма выпускает два набора удобрений для газонов: обычный и улучшенный. В обычный набор входит 3 кг азотных, 4 кг фосфорных и 1 кг калийных удобрений, а в улучшенный – 2 кг азотных, 6 кг фосфорных и 3 кг калийных удобрений. Известно, что для некоторого газона требуется по меньшей мере 10 кг азотных, 20 кг фосфорных и 7 кг калийных удобрений. Обычный набор стоит 3 ден. ед., а улучшенный – 4 ден. ед. Какие и сколько наборов удобрений нужно купить, чтобы обеспечить эффективное питание почвы и минимизировать стоимость?

Вариант 4. На имеющихся у фермера 400 гектарах земли он планирует посеять кукурузу и сою. Сев и уборка кукурузы требует на каждый гектар 200 ден. ед. затрат, а сои – 100 ден. ед. На покрытие расходов, связанных с севом и уборкой, фермер получил ссуду в 60 тыс. ден. ед.. Каждый гектар, засеянный кукурузой, принесет 30 центнеров, а каждый гектар, засеянный соей – 60 центнеров. Фермер заключил договор на продажу, по которому каждый центнер кукурузы принесет ему 3 ден. ед., а каждый центнер сои – 6 ден. ед. Однако, согласно этому договору, фермер обязан хранить убранное зерно в течение нескольких месяцев на складе, максимальная вместимость которого равна 21 тыс. центнеров.

Фермеру хотелось бы знать, сколько гектар нужно засеять каждой из этих культур, чтобы получить максимальную прибыль.

Вариант 5. Продукция двух видов (краска для внутренних (I) и наружных (Е) работ) поступает в оптовую продажу. Для производства красок используются два исходных продукта А и В. Максимально возможные суточные запасы этих продуктов составляют 6 и 8 тонн, соответственно. Расходы продуктов А и В на 1 т соответствующих красок приведены в таблице.

Исходный продукт	Расход исходных продуктов на тонну краски, т			Максимально возможный запас, т
	Краска Е	Краска I
А В	1 2	2 1	6 8

Изучение рынка сбыта показало, что суточный спрос на краску I никогда не превышает спроса на краску Е более чем на 1 т. Кроме того, установлено, что спрос на краску I никогда не превышает 2 т в сутки. Оптовые цены одной тонны красок равны: 3000 ден. ед. для краски Е и 2000 ден. ед. для краски I.

Какое количество краски каждого вида должна производить фабрика, чтобы доход от реализации продукции был максимальным?

Вариант 6. Финансовый консультант фирмы «АВС» консультирует клиента по оптимальному инвестиционному портфелю. Клиент хочет вложить средства (не более 25000$) в два наименования акций крупных предприятий в составе холдинга «Дикси». Анализируются акции «Дикси –Е» и «Дикси –В». Цены на акции: «Дикси –Е» - 5$ за акцию; «Дикси –В» - 3$ за акцию. Клиент уточнил, что он хочет приобрести максимум 6000 акций обоих наименований, при этом акций одного из наименований должно быть не более 5000 штук.

По оценкам «АВС» прибыль от инвестиций в эти две акции в следующем году составит: «Дикси –Е» - 1,1$; «Дикси –В» - 0,9$.

Задача консультанта состоит в том, чтобы выдать клиенту рекомендации по оптимизации прибыли от инвестиций.

Вариант 7. Завод-производитель высокоточных элементов для автомобилей выпускает два различных типа деталей Х и Y. Фонд рабочего времени равен 4000 чел.-ч в неделю. Для производства одной детали типа Х требуется 1 чел./ч, а для производства одной детали типа Y – 2 чел./ч. Производственные мощности завода позволяют выпускать максимум 2250 деталей Х и 1750 деталей Y в неделю. Каждая деталь типа Х требует 2 кг металлических стержней и 5 кг листового металла, а для производства одной детали типа Y необходимо 5 кг металлических стержней и 2 кг листового металла. Уровень запасов каждого вида металла составляет 10000 кг в неделю. Еженедельно завод поставляет 600 деталей типа Х своему постоянному заказчику. По профсоюзному соглашению общее число производимых в течение одной недели деталей должно составлять не менее 1500 штук.

Сколько деталей каждого типа следует производить, чтобы максимизировать общий доход за неделю, если доход от производства одной детали типа Х составляет 30 ден. ед., а от производства одной детали типа Y – 40 ден. ед.?

Вариант 8. Имеется два вида корма I и II, содержащие питательные вещества (витамины) S₁ S₂ и S₃. Содержание числа единиц питательных веществ в 1 кг каждого вида корма и необходимый минимум питательных веществ приведены в таблице:

Питательное вещество (витамин)	Необходимый минимум питательных веществ	Число единиц питательных веществ в 1 кг корма
		I	II
S1 S2 S3	9 8 12	3 1 1	1 2 6

Стоимость 1 кг корма I и II соответственно равна 4 и 6 ден. ед.

Необходимо составить дневной рацион, имеющий минимальную стоимость.

Вариант 9. При производстве двух видов продукции используется 4 типа ресурсов. Норма расхода ресурсов на производство единицы продукции, общий объем каждого ресурса заданы в таблице:

Ресурсы	Норма затрат ресурсов на товары		Общее количество ресурсов
	1-го вида	2-го вида
1 2 3 4	2 1 4 0	2 2 0 4	12 8 16 12

Прибыль от реализации одной единицы продукции первого вида составляет 2 ден. ед., второго вида – 3 ден. ед.

Задача состоит в формировании производственной программы выпуска продукции, обеспечивающей максимальную прибыль от ее реализации.

Вариант 10. Фирма производит вида два безалкогольных напитков – «Лимонад» и «Тоник». Однако объем производства ограничен количеством основного ингредиента и производственной мощностью имеющегося оборудования. Для производства 1 л «Лимонада» требуется 0,02 ч работы оборудования, а для производства 1 л «Тоника» – 0,04 ч. Расход специального ингредиента составляет 0,01 кг и 0,04 кг на 1 л «Лимонада» и «Тоника» соответственно. Ежедневно в распоряжении фирмы имеется 24 ч времени работы оборудования и 16 кг специального ингредиента. Прибыль фирмы составляет 0,10 ден. ед. за 1 л «Лимонада» и 0,30 ден. ед. за 1 л «Тоника».

Сколько продукции каждого вида следует производить ежедневно, если цель фирмы состоит в максимизации ежедневной прибыли?

Задание по теме 3. Нелинейное программирование (НП)

Методические указания по теме 3

Общая постановка задачи НП

Задача нелинейного программирования в общем виде формулируется следующим образом:

Найти

при условиях

где функции f(x₁ , … , x_n), g_i(x₁ , … , x_n), i = 1 , … , m в общем случае нелинейны.

В отличие от задач линейного программирования (ЛП) общего решения задач НП нет.

В задачах ЛП множество допустимых решений выпукло с конечным числом крайних точек. Перебирая их можно за конечной число шагов найти оптимальное решение. В задачах НП выпуклость множество допустимых решений и конечность числа его крайних точек необязательны, из-за чего возникают трудности нахождения решения задачи НП.

Решение задача НП при ограничениях - равенствах

Отыскать минимум ( или максимум ) функции f при таких ограничениях можно с помощью метода множителей Лагранжа.

Идея метода заключается в переходе от исходной задачи нахождения условного экстремума к задаче нахождения безусловного экстремума специально сконструированной функции Лагранжа.

Пусть требуется найти

При ограничениях

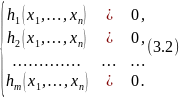
Предположим, что функции f, h₁, h₂, … , h_m дифференцируемы.

Введем набор переменных λ₁, λ₂, … , λ_m ( по числу ограничений ), которые называются множителями Лагранжа и составим функцию Лагранжа следующего вида:

Далее находят частные производные ∂L(x,λ)/ ∂x_j , ∂L(x,λ)/ ∂λ_i и составляют систему из n+m уравнений:

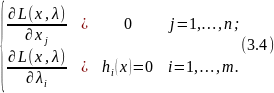
Решая систему уравнений (3.4) находят точку

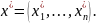
Далее эту точку исследуют на минимум или максимум.

Пример 3.1. Имеется два способа производства некоторого продукта. Обозначим через х₁ и х₂ объемы производства по первой и второй технологиям. Издержки производства по каждой технологии зависят от объемов производства и определяются выражениями:

С точки зрения маркетинга за определенный промежуток времени необходимо произвести строго определенный объем продукции:

h: х₁ + х₂ = С.

Для этого необходимо так спланировать объемы производства х₁ и х₂, чтобы общие издержки производства были минимальны.

Функция Лагранжа для этой задачи имеет вид:

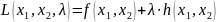
или в развернутом виде

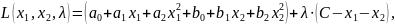
Где первое слагаемое представляет собой целевую функцию f. Дифференцируя функцию Лагранжа по переменным х и λ получаем систему уравнений

Решая эту систему получаем оптимальные (наилучшие) объемы производства x₁^* и x₂^* , обеспечивающие минимум совокупных расходов производства и удовлетворяющие ограничению на общий объем выпуска:

Допустим, что параметры задачи имеют следующие значения :

a0	a1	a2	b0	b1	b2	c
6	2	4	5	3	2	400

Тогда конкретное решение равно:

И оно удовлетворяет ограничению

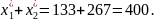
Решение задача НП при ограничениях – неравенствах

Постановка задачи нахождения экстремума выглядит так:

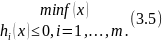
Процедура поиска оптимального решения меняется принципиально.

1. Если минимум функции f лежит внутри области допустимых решений, задаваемых ограничениями h_i , то они не влияют на результат решения, то есть имеет место задача безусловной оптимизации;

2. Если минимум функции f лежит за пределами или на границе области допустимых решений, то часть ограничений участвует в формировании оптимального решения. Эти ограничения называются активными.

Типы функций f и h и характер ограничений определяют многообразие задач НП: выпуклое и вогнутое программирование, квадратичное программирование и т.п.

Путь задача НП задана в виде:

Найти

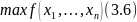
При ограничениях

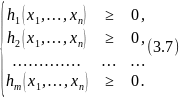
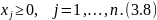
Решение задачи осуществляют по следующей схеме: конструируют функцию Лагранжа описанным выше способом и формируют систему условий ( условия Куна – Таккера ):

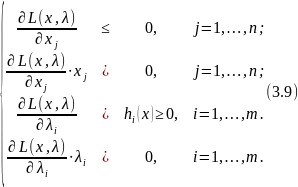
Для нахождения оптимального решения x^* необходимо найти такой вектор λ^* ≥ 0, чтобы выполнялись условия (3.9).

Если функции f и h вогнуты, то условия (3.9) оказываются и достаточными.

Пример 3.2.

Найти

При ограничениях

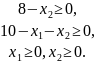
Решение. Так как в данном случае квадратичная форма f(x₁, x₂) вогнута, а ограничения линейны, то имеет место задача квадратичного программирования.

Составим функцию Лагранжа:

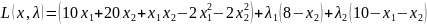
Применив теорему Куна – Таккера получим следующие условия для нахождения оптимального решения:

Последние четыре равенства представляют собой дополнительные условия нежесткости, то есть если первый сомножитель не равен 0, то должен быть равен 0 второй и наоборот. Так если в пятом равенстве х₁ не равно 0, то первое уравнение превращается в равенство и т.д. Таким образом, для нахождения оптимального решения необходимо перебрать все возможные варианты вида:

Выбирается вариант с максимальным значением f и неотрицательными значениями x и λ. В нашем примере оптимальное решение имеет вид:

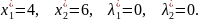
Решение задач нелинейного программирования в MS Excel

Поскольку рассмотренные выше задачи НП имеют единственное решение в силу выпуклости области допустимых решений и унимодальности целевой функции, то их решение может быть легко найдено с помощью табличного процессора MS Excel. Рассмотрим технологию их решения.

Пример 3.3. Найдем решение задачи из примера 3.1. Формальная постановка выглядит следующим образом:

найти

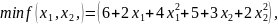
при ограничениях

h: х₁ + х₂ = 400,

х₁ ≥ 0, х₂ ≥ 0.

Решение. Шаблон решения задачи приведен на рис.3.1:

Рис. 3.1. Шаблон решения задачи 3.1 с исходными данными.

Пояснения к рис. 3.1:

Чтобы унифицировать вычисления представим целевую функцию в виде:

Причем х₀₁ = 1, х₀₂ = 1.

Ячейки синего цвета содержат исходные данные:

• в стоке 2 это значения переменных х₀₁ = 1и х₀₂ = 1;

• в строках 4 (B4:G4) и 6 (B6:G6) - это коэффициенты целевой функции f и ограничения h соответственно (пустые ячейки интерпретируются как нули);

Ячейки желтого цвета C2 и F2 отведены под искомые переменные.

В ячейках бежевого цвета размещены расчетные формулы:

Адрес ячейки	Формула
D2	=C2^2
G2	=F2^2
I4	=СУММПРОИЗВ(B2:G2;B4:G4)
I6	=СУММПРОИЗВ(B2:G2;B6:G6)

В главном меню выбираем пункт Данные и нажимаем кнопку Поиск решения и заполняем открывшееся диалоговое окно (рис. 3.2.) и нажимаем кнопку Выполнить:

Рис. 3.2. Исходные данные для запуска процедуры численного решения задачи.

После завершения процедуры процессор сообщит, что решение найдено. Таблица шаблона с результатами решения примет следующий вид:

В ячейках C2 и F2 мы видим оптимальные значения переменных

которые совпадают со значениями, найденные в примере 3.1 методом множителей Лагранжа.

В ячейке I4 число 214 412 означает минимальные общие издержки производства, соответствующие найденной оптимальной структуре выпуска продукции.

Пример 3.4. Найдем решение задачи из примера 3.2. Формальная постановка выглядит следующим образом:

Найти

При ограничениях

Решение. Шаблон решения задачи приведен на рис.3.3:

Рис. 3.3. Шаблон решения задачи 3.2 с исходными данными.

Пояснения к рис. 3.3:

Принципиально структура шаблона не меняется. Ввиду того, что в целевой функции отсутствуют свободные члены, исключены соответствующие переменные х₀₁ и х₀₂ . В ячейках В6, В7 размещены свободные члены ограничений

Ячейки желтого цвета C2 и D2 отведены под искомые переменные c начальными значениями х₁ = 1 и х₂ = 1. Такие начальные значения выбраны с целью простоты проверки правильности вычислений. Поскольку задача имеет один экстремум, то выбор начальной точки на результат решения не влияет. Если в качестве исходной взять точку х₁ = 10 и х₂ = 10 (кстати, лежащую за пределами области допустимых решений), то результат решения не изменится.

В ячейках шаблона размещены следующие расчетные формулы:

Адрес ячейки	Формула
E2	=C1*D1
F2	=C2^2
G2	=D2^2
I4	=СУММПРОИЗВ(C2:G2;C4:G4)
I6	=СУММПРОИЗВ(C2:D2;C6:D6)+B6
I7	=СУММПРОИЗВ(C2:D2;C7:D7)+B7

В главном меню выбираем пункт Данные и нажимаем кнопку Поиск решения и заполняем открывшееся диалоговое окно (рис. 3.4.) и нажимаем кнопку Выполнить:

Рис. 3.4. Исходные данные для запуска процедуры численного решения задачи.

После завершения процедуры процессор сообщит, что решение найдено. Таблица шаблона с результатами решения примет следующий вид:

В ячейках C2 и D2 мы видим оптимальные значения переменных

которые совпадают со значениями, найденные в примере 3.2 c использование условий Куна – Таккера. Значения ячеек I6,I7 показывают, что ограничения h₁ и h₂ выполняются, что свидетельствует о принадлежности оптимального решения области допустимых решений. В ячейке I4 число 80 означает максимальное значение целевой функции.

Контрольные задания по теме 3

Предприятие располагает двумя способами производства данного вида продукции. В течение рассматриваемого периода времени необходимый объем продукции равен В = Х₁ + Х₂, где Х₁ и Х₂ - объемы производства по соответствующему технологическому способу. Затраты производства S при каждом способе зависят от объемов нелинейно:

И(Х₁) = с₀ + с₁ Х₁ + с₂Х₁² , с_0, с_1, с₂  0,

И(Х₂) = р₀ + р₁ Х₂ + р₂Х₂² , р_0, р_1, р₂  0.

Необходимо объем производства так распределить между технологическими способами, чтобы минимизировать общие затраты производства.

Числовые данные для решения задач 1-10 представлены в таблице. Решить задачу двумя способами: методом множителей Лагранжа и с помощью надстройки Поиск решения Excel :

Номер задачи	р0	р1	р2	с0	с1	с2	В
1	5	1	2	3	2	1	100
2	5	1	2	3	2	3	100
3	5	1	1	3	2	1	100
4	1	1	1	1	1	1	100
5	1	2	1	1	1	1	100
6	5	1	2	3	2	1	200
7	5	1	2	3	2	3	200
8	5	1	1	3	2	1	200
9	1	1	1	1	1	1	200
10	1	2	1	1	1	1	200

Задание по теме 4: Методы управления запасами.

Методические указания по теме 4

Основные понятия

Решение проблемы рассматривается на интервале в один год. На примере одного склада с однономенклатурным запасом. Спрос на изделия постоянный. Пополнение запасов может осуществляться либо периодически (циклическая модель), либо при снижении запаса до некоторого уровня (уровневая модель).

Объем заказа – количество заказываемых изделий (размер партии товара).

Повторный уровень заказа – это то количество оставшихся на складе изделий, при котором подается заказ на новую партию.

Время поставки – может быть мгновенным, либо фиксированным, либо случайным.

Штраф за дефицит – это убытки, понесенные из-за неудовлетворенного спроса.

За хранение единицы изделия берется плата C_h. D – годовой спрос на изделия. Стоимость подачи заказа C₀ – это транзакционные издержки по реализации заказа (не зависят от объема заказа). Основная цель построения системы управления запасами – минимизация суммарных издержек.

Основная модель управления запасами

Упрощения модели:

• спрос равномерный и постоянный;

• время поставки постоянно;

• отсутствие запасов недопустимо;

• каждый раз заказывается постоянное количество изделий – оптимальный размер заказа.

Общие издержки обслуживания запасов = издержки пополнения запаса + издержки хранения:

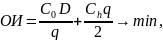
где q – оптимальный объем заказа; q/2 – средний объем хранимого запаса.

Дифференцирование по q и приравнивание производной нулю даст решение:

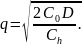
А, В – точки подачи заказа.

Пример 4.1. Годовой спрос D = 1500 ед., стоимость подачи заказа С₀ = 150 рублей/заказ, издержки хранения одной единицы С_h = 45 рублей/год, время доставки 6 дней, 1 год равен 300-стам рабочим дням.

Оптимальный размер заказа:

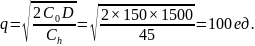
Общие издержки:

За 300 рабочих дней реализуется 1500 единиц, за 6 рабочих дней реализуется 30 единиц. Каждый раз, когда на складе остается 30 единиц товара, подается заявка на 100 единиц.

За год будет подано 1500/100 = 15 заказов (за год пройдет 15 циклов). Расстояние между циклами 1/15 лет = 20 дней.

Модель экономического размера партии

Используется в тех случаях, когда процесс производства представляет собой последовательность периодов равномерных производства и реализации. Каким в этом случае должен быть размер заказа q ?

Обозначим через C_s стоимость организации производственного цикла, тогда общие издержки

Общие издержки обслуживания запасов = стоимость организации производственного цикла + издержки хранения:

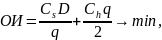
где q – экономичный размер партии производства.

Решение задачи имеет вид:

Пример 4.2. Годовой спрос D = 14800 ед., стоимость организации производственного цикла С_s = 100 рублей/, издержки хранения одной единицы С_х = 8 рублей/год.

Экономичный размер партии равен:

То есть надо произвести 608 единиц, остановить производство, реализовать всю произведенную продукцию и вновь запустить производство и т.д.

Издержки

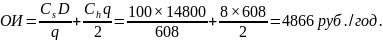
Число циклов за год D / q = 14800/608 = 24.3. Интервал между циклами q / D = 0,04 года = 15 дней.

Учет скидки на объем заказа

Очень часто, если объем заказа больше определенного уровня, поставщик предоставляет скидку. В этом случае снижаются расходы на закупку, но увеличиваются затраты на хранение.

,

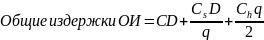где С – закупочная цена.

Необходимо выяснить, стоит ли воспользоваться скидкой.

Пример 4.3. Годовой спрос D = 1000 ед., стоимость подачи заказа С₀ = 40 рублей / заказ, закупочная цена С = 50 рублей за единицу, годовая стоимость хранения одной единицы составляет 25% от её цены. Можно получить скидку 3%, если размер заказа будет не менее 200 единиц. Стоит ли воспользоваться скидкой ?

Стоимость хранения одной единицы C_h = 0,25С = 0,2550 = 12,5 рублей за единицу.

Найдем оптимальный размер заказа:

Общие издержки в случае основной модели равны:

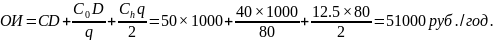
Если воспользоваться скидкой, то новая закупочная цена равна: С = 0,9750 = 48,5 рублей / единицу.

Поэтому C_h = 0,25С = 0,2548,5 = 12,125 рублей за единицу.

В этом случае оптимальный размер заказа равен:

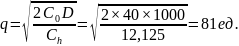
Но скидка предоставляется, если q  200. Поэтому полагаем q = 200.

Тогда общие издержки равны:

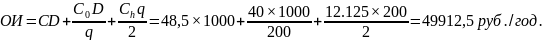
Мы видим, что общие издержки уменьшились, поэтому следует воспользоваться скидкой, заказывая каждый раз 200 единиц.

Число циклов за год D / q = 1000 / 200 = 5. Интервал между циклами q / D = 200 / 1000 = 1 / 5 года = 73 дня.

Модель производства партии продукции

Ранее была рассмотрена модель экономичного размера партии из условия, что чередуются производство и потребление. В предлагаемой модели технология предполагает последовательные этапы производства и потребления, потребление допускается при появлении готовой продукции, т.е. в течение производственного цикла.

Пусть Р – темп производства, D – темп использования продукции. Произведя q единиц продукции, производство останавливаем. Так как параллельно с производством продукция потреблялась, то в момент остановки на складе продукции будет меньше, чем q.

Общие издержки обслуживания запасов = стоимость организации производственного цикла + издержки хранения:

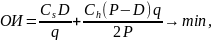
где q – экономичный размер партии производства.

Решение задачи имеет вид:

Пример 4.4. Компания выпускает сувениры. В среднем она может производить 150 сувениров в день. Спрос на сувениры 40 штук в день. Годовые издержки хранения – 8 рублей за сувенир. Стоимость организации производственного цикла – 100 рублей. Найти экономичный размер партии, издержки, число циклов за год и интервалы между циклами.

Решение: Р = 150 изд. / день = 54 750 изд. / год., D = 40 изд. / день = 14 600 изд. / год.

Экономичный размер партии:

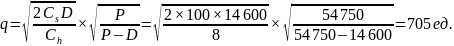
Издержки равны:

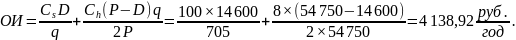
Таким образом, произведя 705 сувениров, останавливаем производство. Параллельно с момента начала производства реализуем сувениры. Как только сувениры закончатся, тут же запускаем производственный процесс. Число циклов за год D / q = 14 600 / 705 = 20,7. Интервал между циклами q / D = 705 / 14 600 = 0,048 года = 18 дней.

Модель планирования дефицита

Иногда издержки хранения очень высоки. Целесообразно допустить . наличие дефицита в отдельные промежутки времени.

Общие издержки ОИ = издержки подачи заказа + издержки хранения +штраф за дефицит.

Возможны два подхода:

1. полученная новая продукция не идет на погашение дефицита;

2. часть продукции идет на погашение всех заявок, оставленных во время отсутствия товаров.

Рассмотрим эти случаи.