
Экзаменационные задачи по модулю «Теория электромагнитного поля»
1. Уравнения электромагнитного поля
Задача 1.1.
По цилиндрическому проводу радиусом 2 см протекает электрический ток 31,4 А. Определить модуль rotH внутри проводника.
Задача 1.2.
Индукция магнитного поля в бесконечно длинном проводе круглого сечения радиусом R=2см направлена по оси провода и меняется по закону Bz=1+0.1sin(314t ) Тл.
Определить модуль rotE при R=1см.
Задача 1.3.
Плоский воздушный конденсатор, состоящий из двух круглых пластин радиуса r0=2 см, отдаленных друг от друга на расстояние d=1мм, находится под напряжением u=200sin(2π·106t) B.Пренебрегая краевым эффектом, определить плотность тока смещения.
Задача 1.4.
Плоский конденсатор с диэлектрической проницаемостью εr=3.14, γ=10-8См/м и d=1 см подключен под синусоидальное напряжение u(t)=200sin(360t+45º) B. Определить выражение мгновенной плотности тока в конденсаторе. Краевым эффектом пренебречь.
Задача 1.5.
Вдоль оси z цилиндрической системы координат в воздухе расположен длинный цилиндрический прямолинейный провод с радиусом r0 и абсолютной магнитной проницаемостью μ; вдоль повода протекает постоянный ток I.
Интегрируя уравнение rotH=j, определить вектор H внутри провода.
В
цилиндрической системе координат

Задача 1.6.
Найти rotE в точке находящейся на расстоянии r0=0.2 м от линейного бесконечно длинного проводника с током i=14,1sin105t А. Проводник расположен в воздухе.
Задача 1.7.
Плоский воздушный конденсатор, состоящий из двух круглых пластин радиуса r0=2 см, отдаленных друг от друга на расстояние d=1мм, находится под напряжением u=200sin(2π·106t) B.Пренебрегая краевым эффектом, определить зависимость напряженности магнитного поля от расстояния r от центра пластин (при 0≪r≪ r0).
а) H= Hα =r·11,1cos(2π·106t ) А/м2 б) H= Hα =r·5,5cos(2π·106t ) А/м2
в) H=Hα=5,5sin(2π·106t ) А/м2 г) H=Hz=11,1·rcos(2π·106t ) А/м2
Задача 1.8.
Индукция магнитного поля в бесконечно длинном проводе круглого сечения радиусом R=2см направлена по оси провода и меняется по закону Bz=1+0.1sin(314t ) Тл
Интегрируя
уравнение
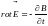 ,
определить
вектор E
внутри провода.
,
определить
вектор E
внутри провода.
В цилиндрической
системе координат

Задача 1.9.
Бесконечно длинная стальная пластина, ширина d которой много больше ее толщины h, расположена в плоскости y=0, нормальной к линиям индукции =Bmsinωt однородного магнитного поля. Определите зависимость плотности jz(x) тока по ширине пластины при допущении, что магнитная индукция, обусловленная индуцированным в пластине током, значительно меньше Bm. Удельная электрическая проводимость стали равна 106 См/м. рассчитайте ток в пластине при d=5 см, h=2 мм, Bm =0.001 Тл, ω =314 с-1.
Задача 1.10.
Определите зависимость плотности jz(x) тока, индуцированного в тонком стальном диске, толщина h, которого много меньше радиуса R и плоскость которого перпендикулярна линиям индукции B= Bmsinωt внешнего однородного поля при допущении, что индукция, созданная индуцированным в диске током, много меньше индукции внешнего магнитного поля. Удельная электрическая проводимость стали равна 106 См/м. Bm=0.001 Тл, ω=314 с-1.
