23

Физика (заочники)

Раздел 2. Молекулярная физика и основы термодинамики

Тема №2. Основные представления молекулярно - кинетической теории (МКТ) газов. Физические основы термодинамики

Вопросы:

1. Основные представления МКТ-газов.

2. Физические основы термодинамики.

3. Реальные газы.

1. Основные представления мкт – газов

Существует два способа описания процессов, происходящих в макроскопических телах – статистический и термодинамический.

Макроскопическим телом называется тело, состоящее из очень большого числа частиц - атомов или молекул.

В огромной совокупности молекул возникают качественно новые закономерности, называемые статистическими.

Эти закономерности утрачивают смысл при переходе к системам с малым числом частиц.

Статистическая физика изучает статистические закономерности.

Она использует вероятностные методы и истолковывает свойства тел, непосредственно наблюдаемые на опыте (давление, температура), как суммарный, усредненный результат действия отдельных молекул.

Термодинамика же изучает свойства макроскопических тел и протекающие в них процессы, не вдаваясь в микроскопическую природу тел.

В основе термодинамики лежит 3 фундаментальных закона, называемые началами термодинамики, которые были установлены в результате обобщения очень большого количества опытных фактов.

Поэтому результаты, получаемые термодинамикой, имеют весьма общий характер.

Статистическая физика и термодинамика взаимно дополняют друг друга и образуют единое целое.

Молекулярно-кинетические представления

Всякое вещество состоит из молекул.

Молекула – мельчайшая частица вещества, сохраняющая некоторые его свойства.

В состав молекул входят атомы – мельчайшие частицы химического элемента, сохраняющие его химические свойства.

Для измерения количества вещества вводится единица – моль. В одном моле любого вещества содержится одинаковое количество молекул

N_a = 6,022 × 10 ²³ 1/моль (число Авогадро).

При нормальных условиях 1 моль любого газа, занимает объем

.

Нормальные условия:

Температура T_o = 273 K (0˚C).

Давление P_o = 1,013 10⁵ Па (760 мм рт. ст.)

Все молекулы находятся в хаотическом движении, которое называется тепловым.

Термодинамической системой называется совокупность макроскопических тел, которые могут обмениваться между собой и внешней средой энергией.

Термодинамическая система может находиться в различных состояниях, отличающихся температурой, давлением, объемом, плотностью и др.

Величины, характеризующие состояние систем называются параметрами состояния.

Соотношение, устанавливающее связь между параметрами состояния какого-либо тела, называется уравнением состояния этого тела.

В простейшем случае равновесное состояние тела определяется значениями трёх параметров:

1. Давления P, Па;

2. Объема V, м³;

3. Температуры T, K.

Идеальный газ – это газ, размерами его молекул пренебрегают, не учитывается взаимодействие между молекулами.

Для 1 моля идеального газа уравнение состояния

– уравнение Клапейрона, (1)

где P – давление;

– объем 1 моля газа;

температура, К;

R = 8, 31 Дж / (моль К) – универсальная газовая постоянная.

Для m, кг газа:

– Уравнение Менделеева Клапейрона, (2)

где V – объём газа;

m – масса газа;

= m/ µ - число молей;

µ - молярная масса газа, кг / моль.

Пример: O₂ → µ = 32 10 ^{– 3} кг / моль.

Н₂ → µ = 2 10 ^{– 3} кг / моль.

СO₂ → µ = 44 10 ^–3 кг / моль.

Дж / К – постоянная Больцмана.

Из (2), можно получить другую запись уравнения Клапейрона – Менделеева (уравнения состояния):

(3)

где – число молекул в единице объема;

число молекул газа;

объем газа.

При поступательном движении молекул и ударе их о стенку сосуда, давление, которое они создают

,

– средняя энергия поступательного движения молекулы.

Средняя энергия молекулы

из (3) и (4) следует, что

(5)

Из (5) получаем, что термодинамическая температура есть величина пропорциональная средней энергией поступательного движения молекул.

Только поступательно движутся лишь одноатомные молекулы.

Двух – и многоатомные молекулы, кроме поступательного, могут совершать также вращательное и колебательное движения.

Эти виды движения связаны с некоторым запасом энергии, который можно вычислить на основании закона распределения энергии по степеням свободы молекулы.

Числом степеней свободы механической системы называется количество независимых величин, с помощью которых может быть задано положение системы в пространстве.

Система из N материальных точек, между которыми нет жестких связей, имеет 3 N степеней свободы.

Каждая жесткая связь, устанавливающая неизменное расстояние между двумя материальными точками, уменьшает число степеней свободы на единицу.

Если между материальными точками действует квазиупругая сила (подобная F_упр. в пружине), то такая степень свободы называется колебательной.

Упругая связь не уменьшает число степеней свободы.

Число колебательных степеней свободы равно 3N – 6.

На каждую поступательную степень свободы приходится энергия, равная

Согласно закону распределения:

На каждую степень свободы (поступательную, вращательную и колебательную) в среднем приходится одинаковая кинетическая энергия, равная .

Колебательная степень свободы молекулы обладает удвоенной энергетической емкостью – на каждую колебательную степень свободы приходится в среднем две половинки kT – одна в виде кинетической энергии и одна в виде потенциальной энергии.

Средняя энергия молекулы:

где =

Внутренняя энергия газа:

.

F(v) – функция распределения вероятности значений v.

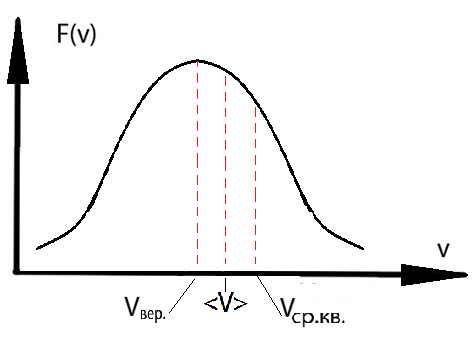
(6)

.

масса одной молекулы газа.

Барометрическая формула

(7)

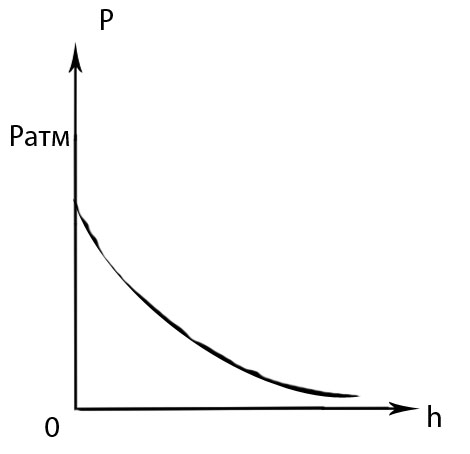
P₀ – давление воздуха на высоте, принятой за начало отсчета.

Распределение Больцмана

(8)

плотность молекул (число молекул в единице объёма) ;

n ₀ – плотность молекул в том месте, для которого принято равной нулю;

потенциальная энергия молекулы.

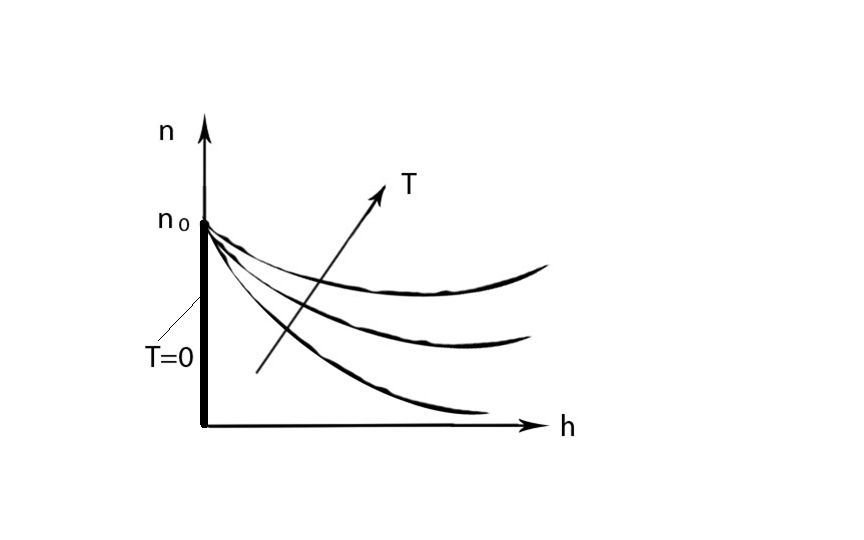
Явления переноса

Длина свободного пробега молекул – это среднее расстояние, которое проходят молекулы между двумя последовательными соударениями.

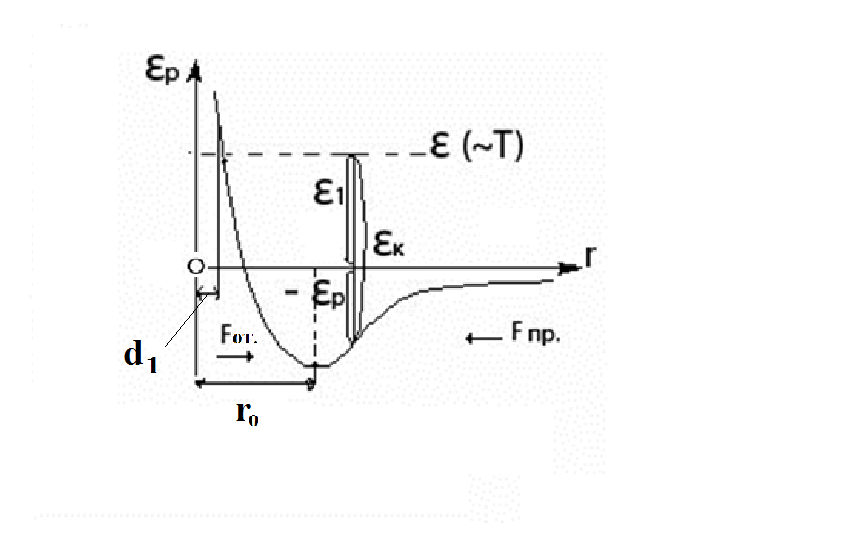
взаимная потенциальная энергия.

.

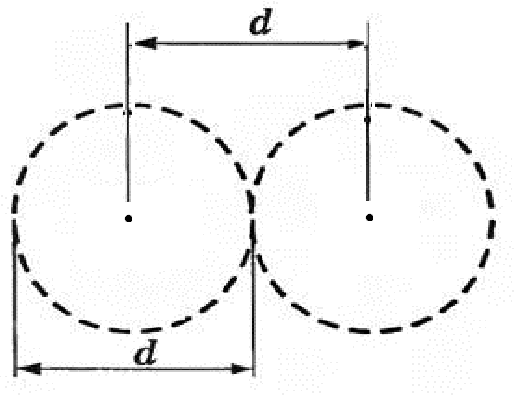
d – эффективный диаметр молекулы – это то расстояние, на которое сближаются центры молекул при столкновении.

– эффективное сечение молекулы.

. (9)

. (10)

  – среднее число соударений в единицу времени.

кг/с – 1-й закон Фика. (11)

массовый поток.

<v> – коэффициент диффузии (отнесенный к разности плотностей), м²/с.

– уравнение Фурье (12)

q – тепловой поток, Вт;

– коэффициент теплопроводности, Вт/(м )

– уравнение Ньютона (13)

(реологический закон течения).

F сила внутреннего трения;

η – динамический коэффициент вязкости ,