Вариант 7

1 Задание: найдите AB, BA, AC, :

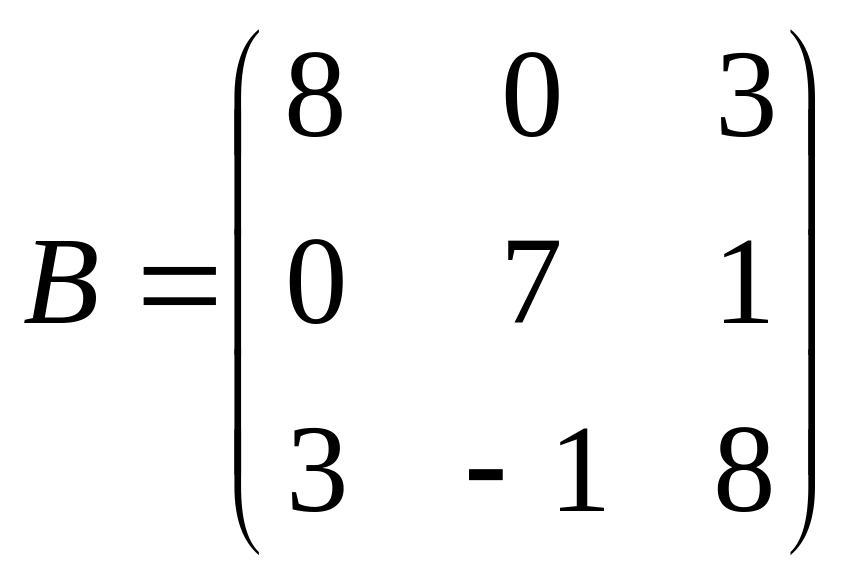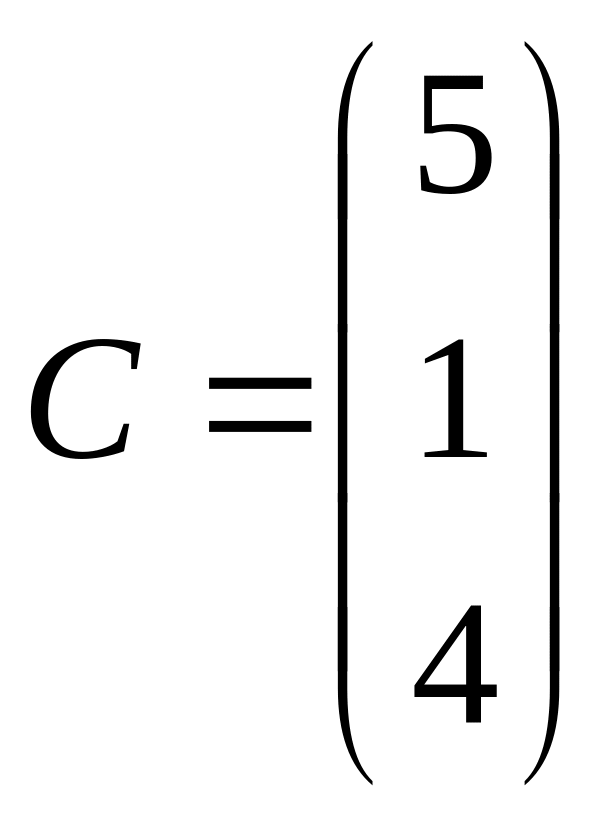; ; ; где , «?» - порядковый номер по журналу

2 Задание. Вычислить определитель

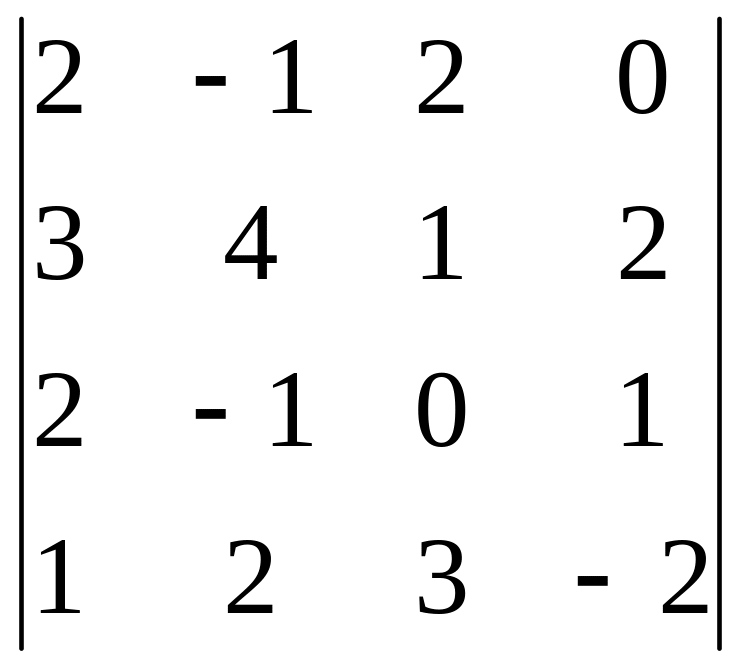
3 Задание. Найти ранг матрицы

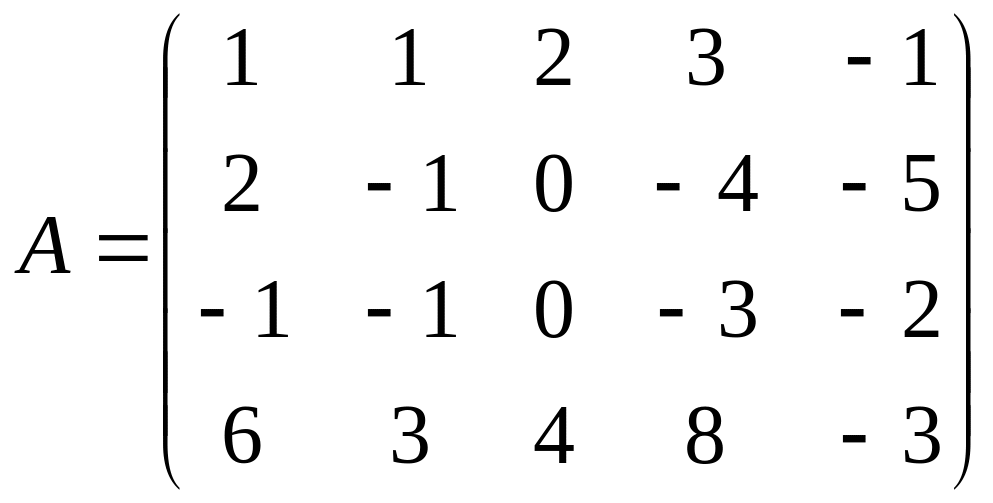
4 Задание. Исследовать на совместность, найти решение системы уравнений

а) методом Крамера;

б) с помощью обратной матрицы.

Сделайте проверку полученного решения.

5 Задание. Найти многочлен 3-ей степени f (x) , для которого

f (1) = 6 , f (−1) = 2, f (2) = 20 , f (−3) = −10.

6 Задание. Докажите, что векторы , , образуют базис и найдите разложение вектора по векторам , , если , , , .

7 Задание Для производства продукции пяти видов в количестве 20 , 30 , 28 , ? , 56 соответственно предприятие тратит сырье в количестве 2 , 3 , 4 , 2 , 3 кг на ед. продукции соответственно. Составить вектор объема производства и затрат сырья на ед. продукции, определить общие затраты сырья, определите стоимость сырья на производство продукции, если 1 кг сырья стоит 25руб.

«?» - порядковый номер по журналу

8 Задание. В декартовой прямоугольной системе координат даны 3 точки:

А(3,0,-1), В(-1,-2,-4), С(-1,2,4).

Найдите:

а) длину отрезка АВ и координаты точки М – середины этого отрезка;

б) уравнение прямой АВ и прямой ВС;

в) угол между прямыми АВ и ВС;

г) уравнение плоскости АВС.

Вариант 8

1 Задание: найдите AB, BA, AC, :

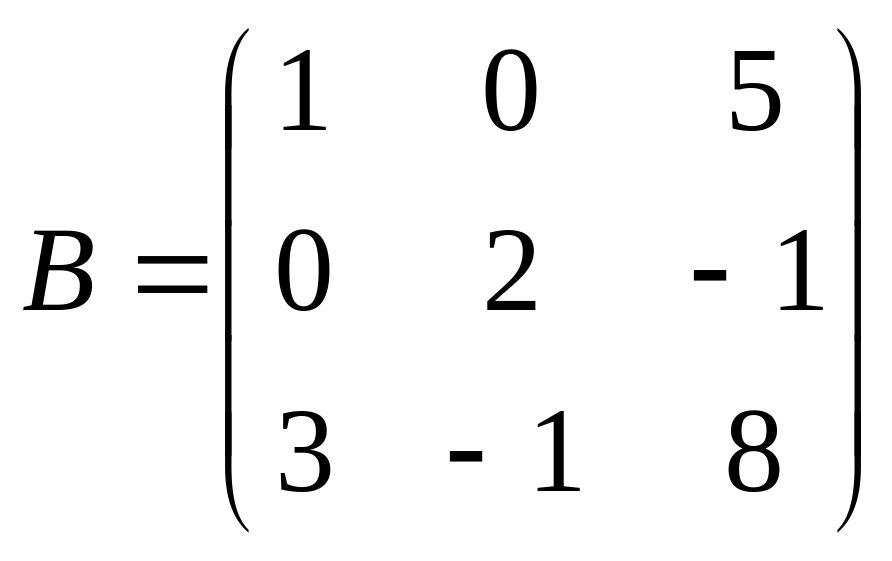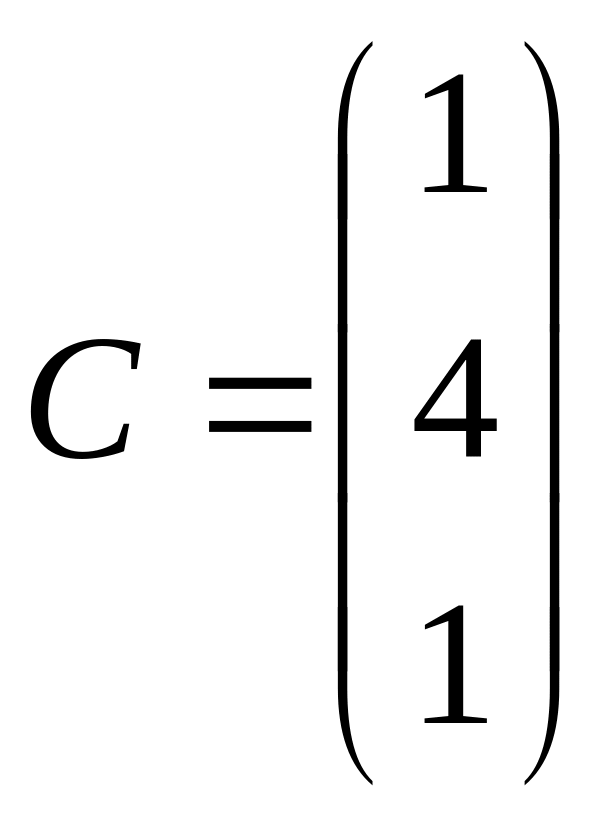; ; ; где , «?» - порядковый номер по журналу

2 Задание. Вычислить определитель

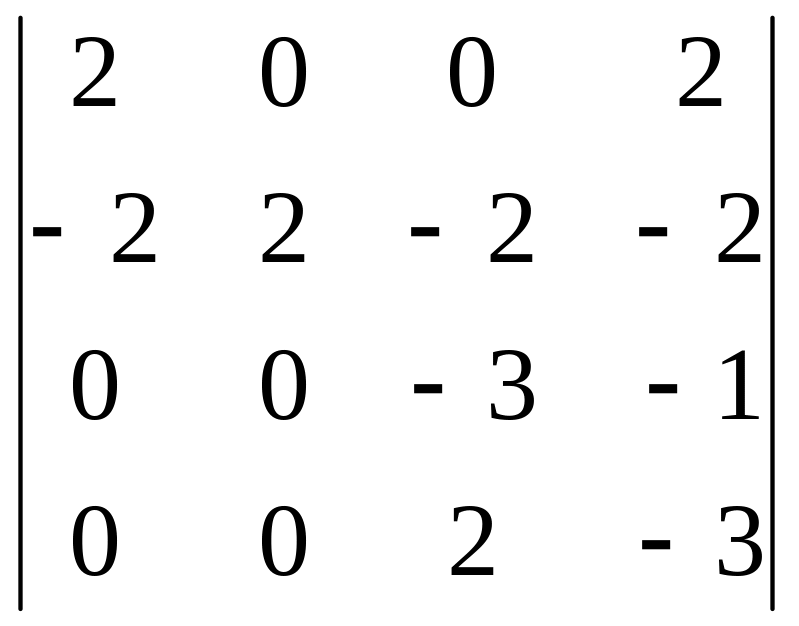
3 Задание. Найти ранг матрицы

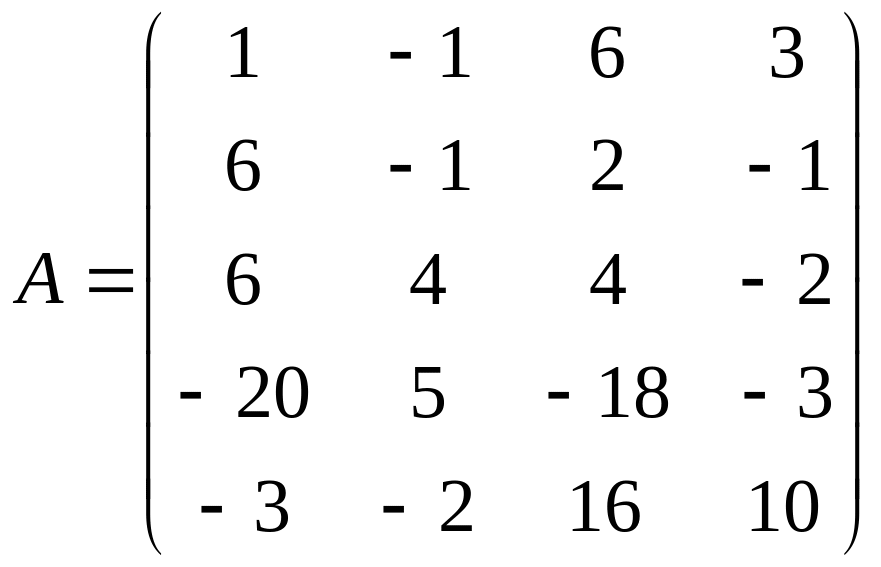
4 Задание. Исследовать на совместность, найти решение системы уравнений

а) методом Крамера;

б) с помощью обратной матрицы.

Сделайте проверку полученного решения.

5 Задание. Найти многочлен 3-ей степени f (x) , для которого

f (1) = −4 , f (−1) = −8, f (2) = −10, f (−2) = −25.

6 Задание. Докажите, что векторы , , образуют базис и найдите разложение вектора по векторам , , если , , , .

7 Задание Комбинат железобетонных изделий производит продукцию пяти видов в объеме 63 , 75 65 , ? , 60 тонн соответственно за год. Себестоимость производства одной тонны продукции 100, 110, 98, 64, 76 тыс. руб. соответственно. Составить вектор объема производства, себестоимости. Определить общие затраты на производство продукции, а также объемы производства каждого вида продукции за 5 лет.

«?» - порядковый номер по журналу

8 Задание. В декартовой прямоугольной системе координат даны 3 точки:

А(2,-2,1), В(1,2,-1), С(1,0,2).

Найдите:

а) длину отрезка АВ и координаты точки М – середины этого отрезка;

б) уравнение прямой АВ и прямой ВС;

в) угол между прямыми АВ и ВС;

г) уравнение плоскости АВС.

Вариант 9

1 Задание: найдите AB, BA, AC, :

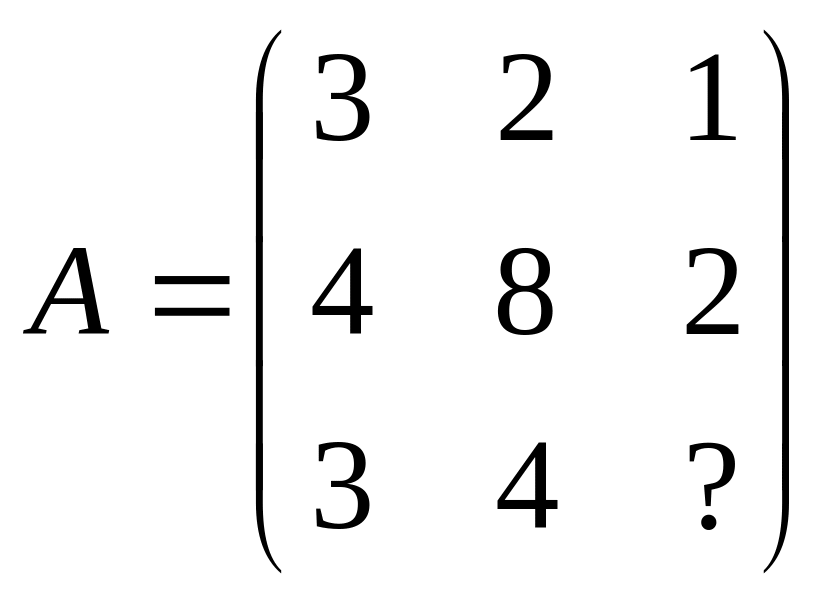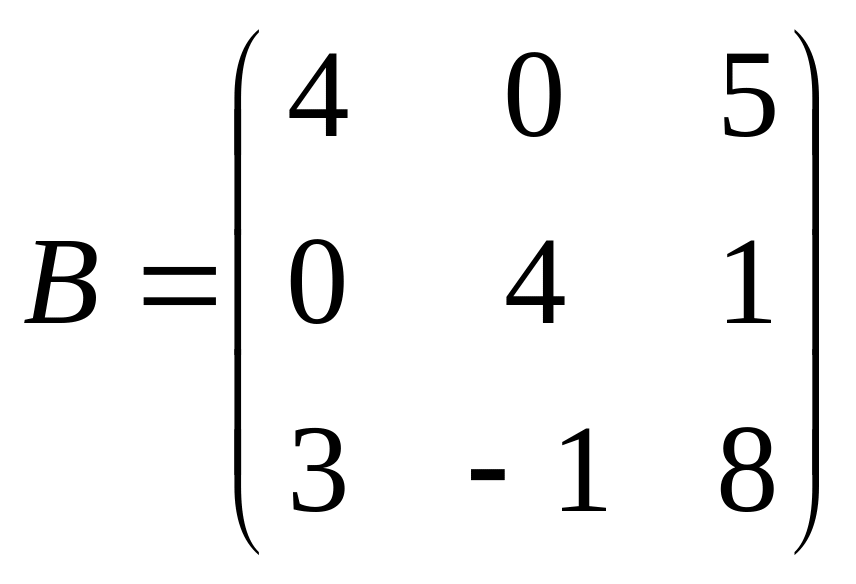; ; ; где , «?» - порядковый номер по журналу.

2 Задание. Вычислить определитель

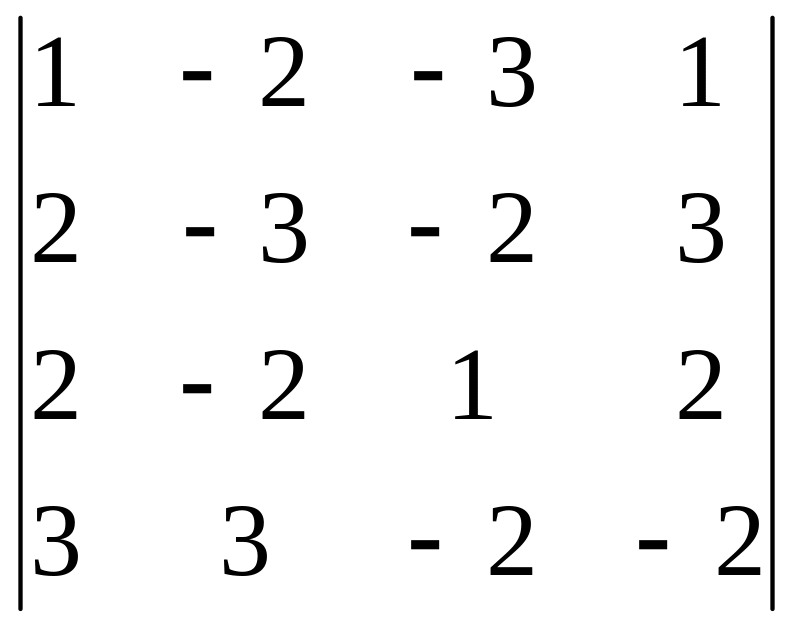
3 Задание. Найти ранг матрицы

4 Задание. Исследовать на совместность, найти решение системы уравнений

а) методом Крамера;

б) с помощью обратной матрицы.

Сделайте проверку полученного решения.

5 Задание. Найти многочлен 3-ей степени f (x) , для которого

f (1) = 8, f (−1) = 4, f (2) = 25 , f (−2) = 5..

6 Задание. Докажите, что векторы , , образуют базис и найдите разложение вектора по векторам , , если , , , .

7 Задание Лицей осуществляет набор школьников в 7-11 классы. Количество 7,8,9 классов - по два, десятых и одиннадцатых классов – по три. Максимальная наполняемость 7-9-ых классов составляет ? человек, 10-х – 30 человек, 11-х – 28 человек. Составить вектора количества классов, численности школьников в них. Определить максимальную численность школьников в лицее. Определить затраты на подготовку всех школьников, если затраты на одного составляют 1000 руб.

«?» - порядковый номер по журналу

8 Задание. В декартовой прямоугольной системе координат даны 3 точки:

А(1,-1,1), В(2,1,-1), С(-2,0,3).

Найдите:

а) длину отрезка АВ и координаты точки М – середины этого отрезка;

б) уравнение прямой АВ и прямой ВС;

в) угол между прямыми АВ и ВС;

г) уравнение плоскости АВС