Вариант 4
1 Задание: найдите AB, BA, AC, :
;
;
;
,
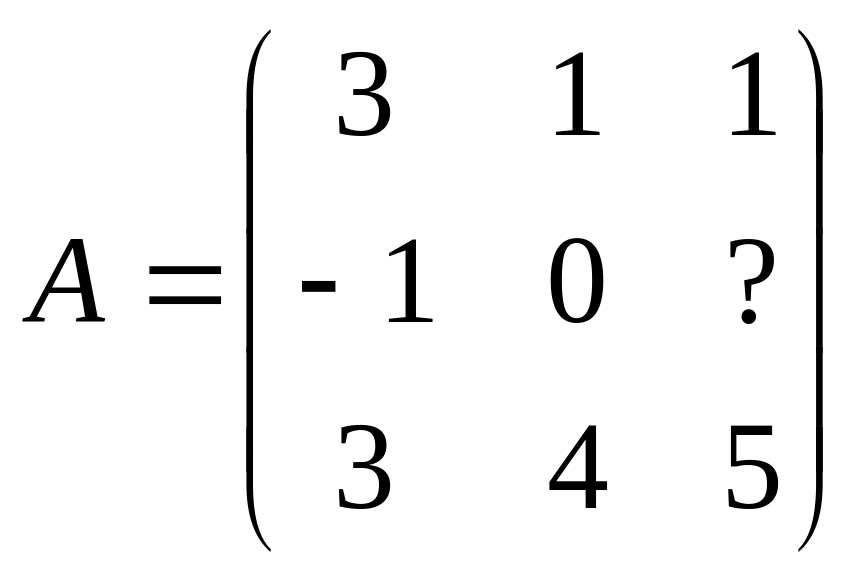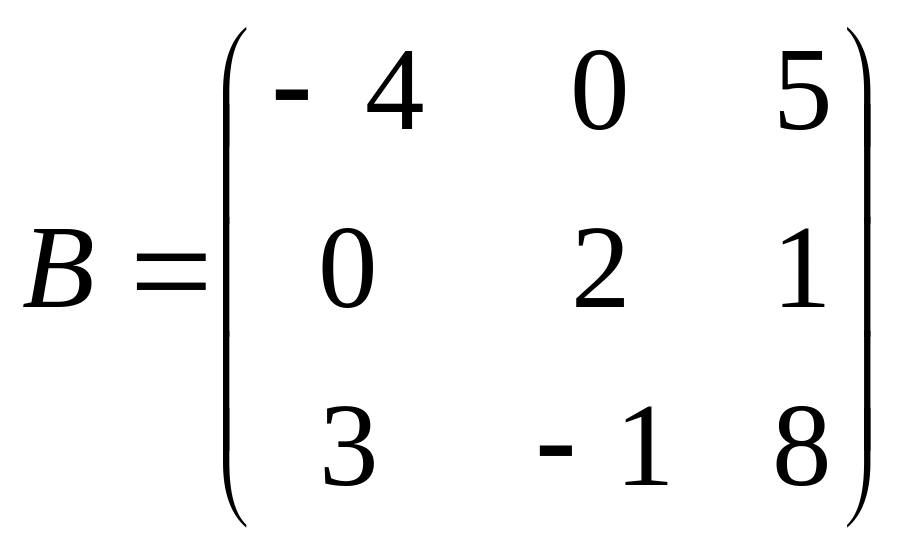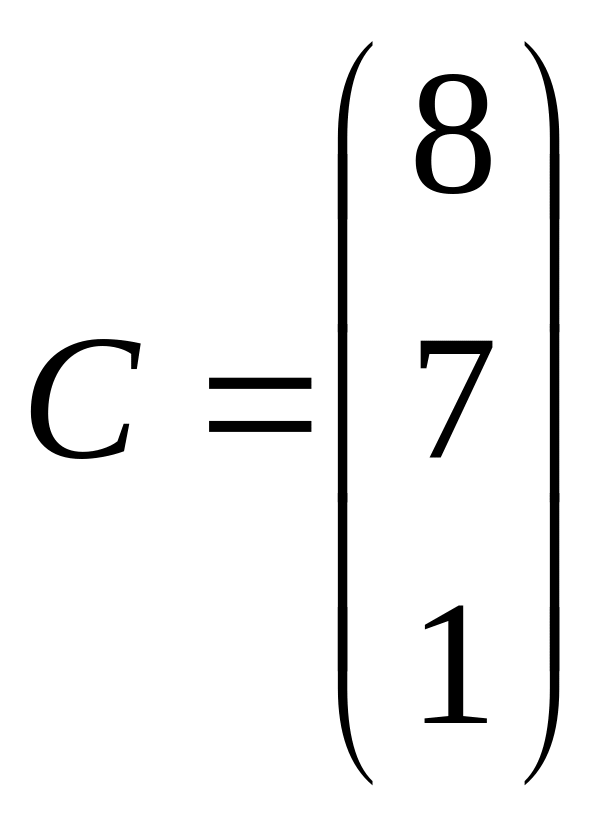где «?»
- порядковый номер по журналу
2 Задание. Вычислить определитель
3 Задание. Найти ранг матрицы
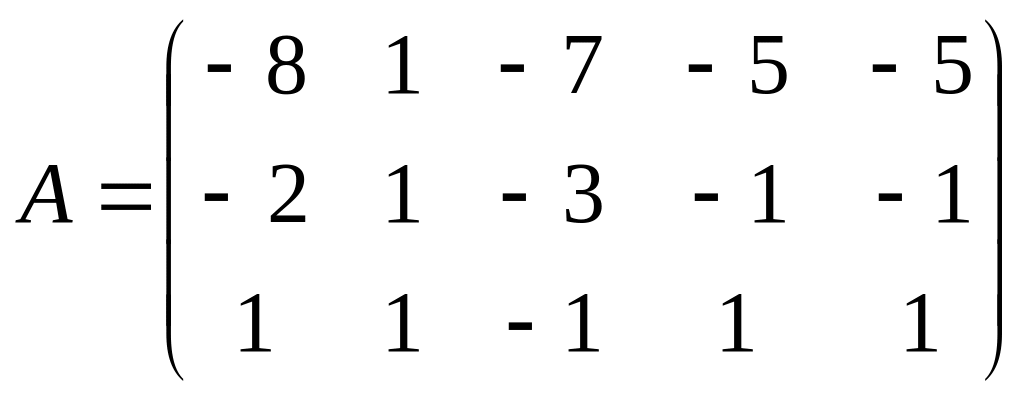
4 Задание. Исследовать на совместность, найти решение системы уравнений
а) методом Крамера;
б) с помощью обратной матрицы.
Сделайте проверку полученного решения.
5 Задание. Найти многочлен 3-ей степени f (x) , для которого
f (−2) = −15 , f (−1) = −4, f (2) = 5, f (3) = 20 .
6
Задание.
Докажите, что векторы
,
,
образуют
базис
и
найдите
разложение
вектора
по
векторам
,
,
если
,
,
,
.
7 Задание Домостроительный комбинат реализует квартиры пяти типов в количестве 23 , 25 , 15 , ? , 20 соответственно. Площади квартир равны 100, 110, 98, 64, 76 кв.м. Цена одного квадратного метра равна 1100 долл. Составить вектор объема реализации квартир и их площадей, определить общую площадь всех квартир, предлагаемых к продаже, определить стоимость квартир каждого типа и общую стоимость.
«?» - порядковый номер по журналу
8 Задание. В декартовой прямоугольной системе координат даны 3 точки:
А(1,1,4), В(2,1,2), С(1,-1,2)
Найдите:
а) длину отрезка АВ и координаты точки М – середины этого отрезка;
б) уравнение прямой АВ и прямой ВС;
в) угол между прямыми АВ и ВС;
г) уравнение плоскости АВС.
Вариант 5
1 Задание: найдите AB, BA, AC, :
;
;
;
,
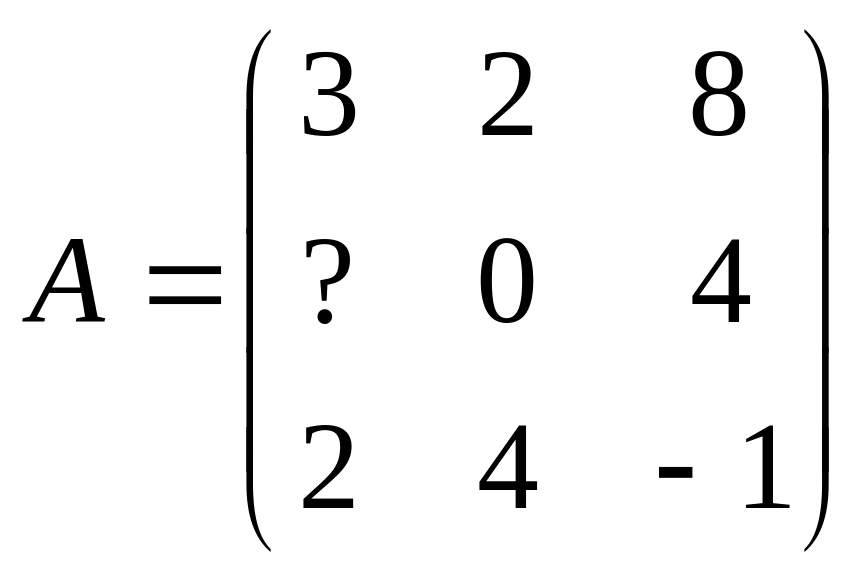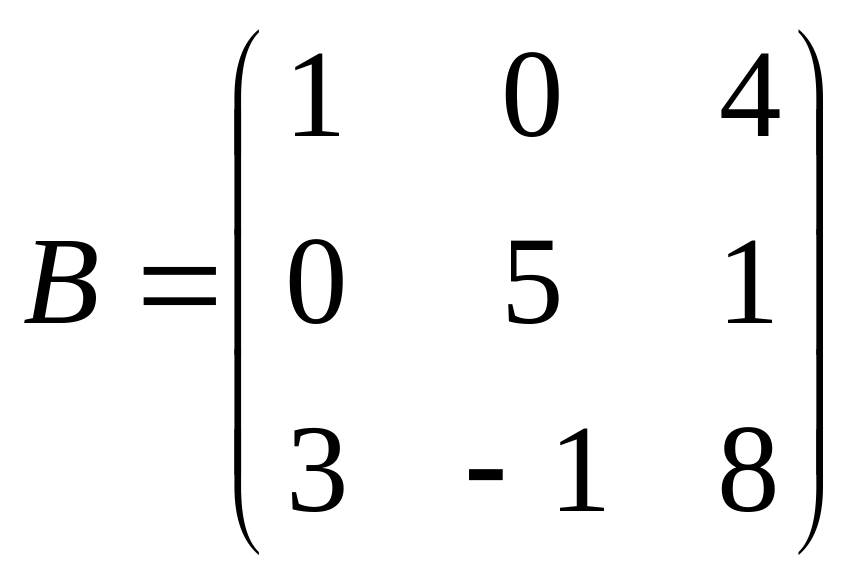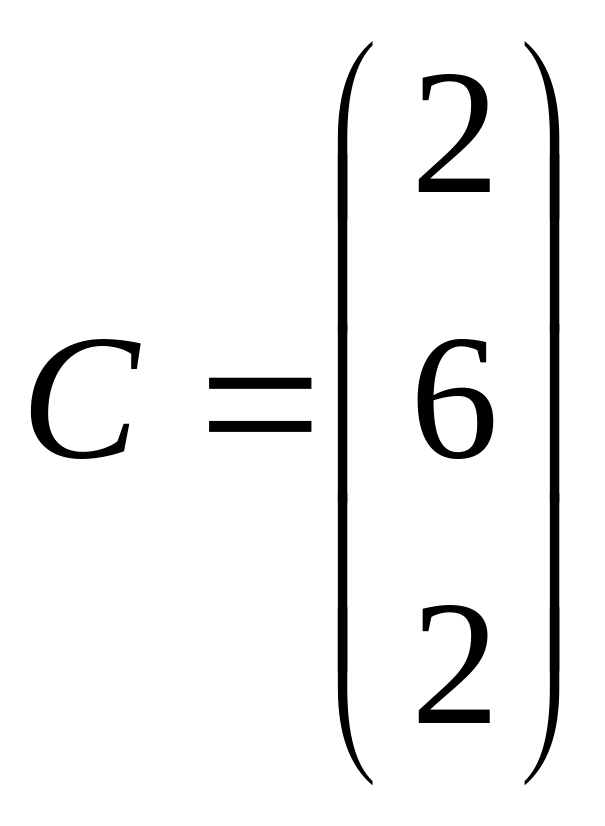где «?»
- порядковый номер по журналу
2 Задание. Вычислить определитель
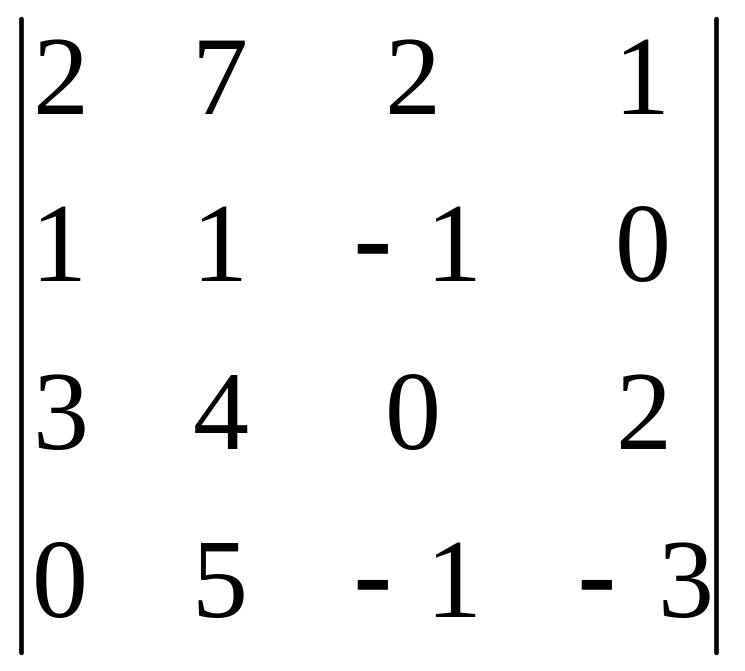
3 Задание. Найти ранг матрицы
4 Задание. Исследовать на совместность, найти решение системы уравнений
а) методом Крамера;
б) с помощью обратной матрицы.
Сделайте проверку полученного решения.
5 Задание. Найти многочлен 3-ей степени f (x) , для которого
f (−3) = −20 , f (−2) = −5, f (2) =15, f (1) = 4.
6
Задание.
Докажите, что векторы
,
,
образуют
базис
и
найдите
разложение
вектора
по
векторам
,
,
если
,
,
,
.
7 Задание На предприятии работают служащие пяти категорий в количестве 12, 15, 21, ?, 25 человек соответственно. Заработная плата работников равна 5670,7800,8230,9450,10210 руб. соответственно. Составить вектор численности сотрудников, вектор заработной платы, определить фонд заработной платы, как изменится фонд заработной платы, если число сотрудников первой категории увеличилось вдвое, а сотрудников третьей категории уменьшилось на 20%.
«?» - порядковый номер по журналу
8 Задание. В декартовой прямоугольной системе координат даны 3 точки:
А(2,1,-4), В(-3,-5,6), С(0,-3,-1).
Найдите:
а) длину отрезка АВ и координаты точки М – середины этого отрезка;
б) уравнение прямой АВ и прямой ВС;
в) угол между прямыми АВ и ВС;
г) уравнение плоскости АВС.
Вариант 6
1 Задание: найдите AB, BA, AC, :
;
;
;
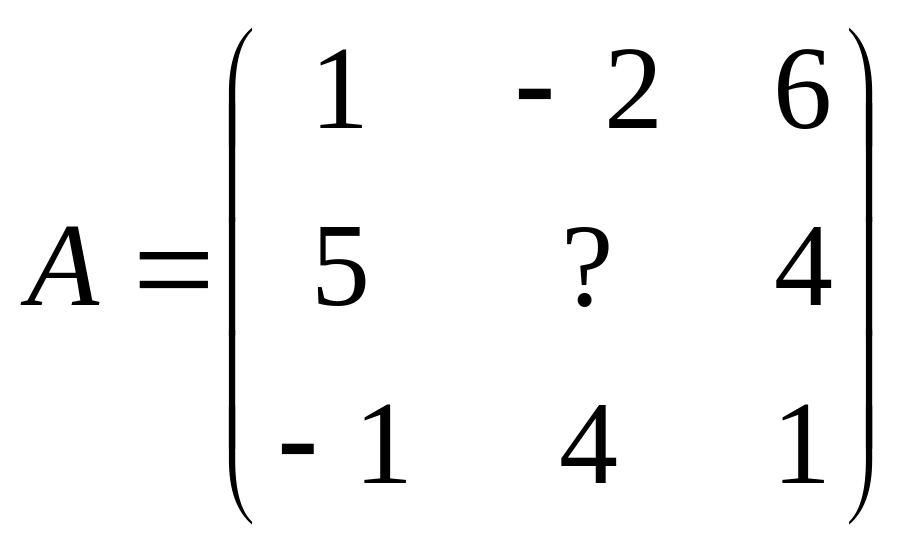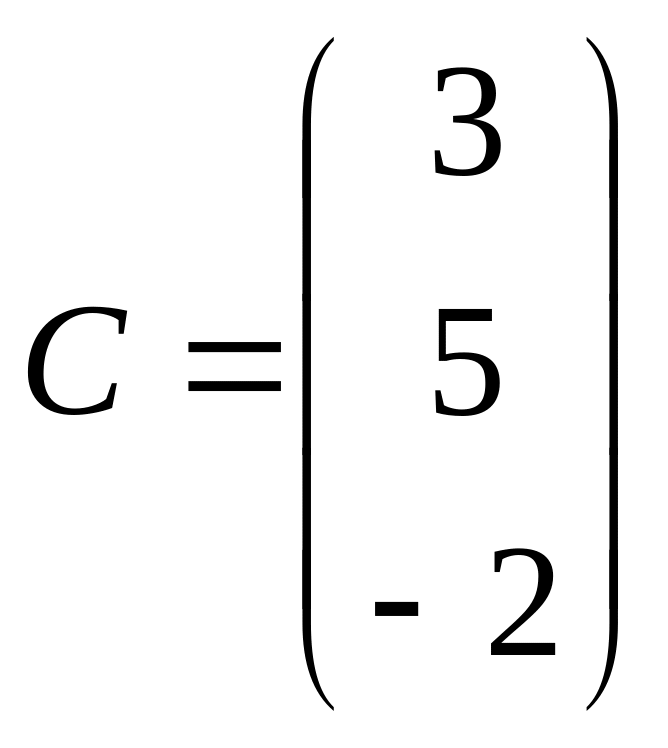где
,
«?»
- порядковый номер по журналу
2 Задание. Вычислить определитель
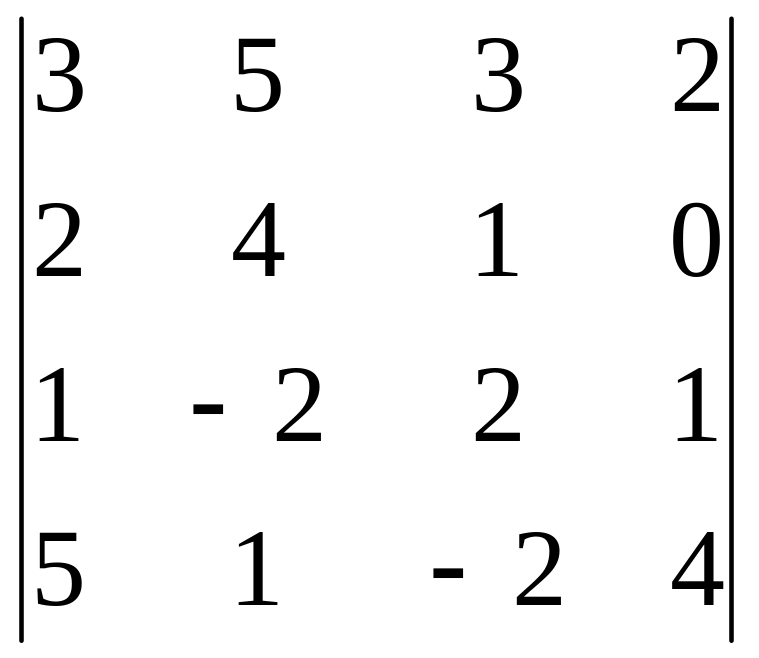
3 Задание. Найти ранг матрицы
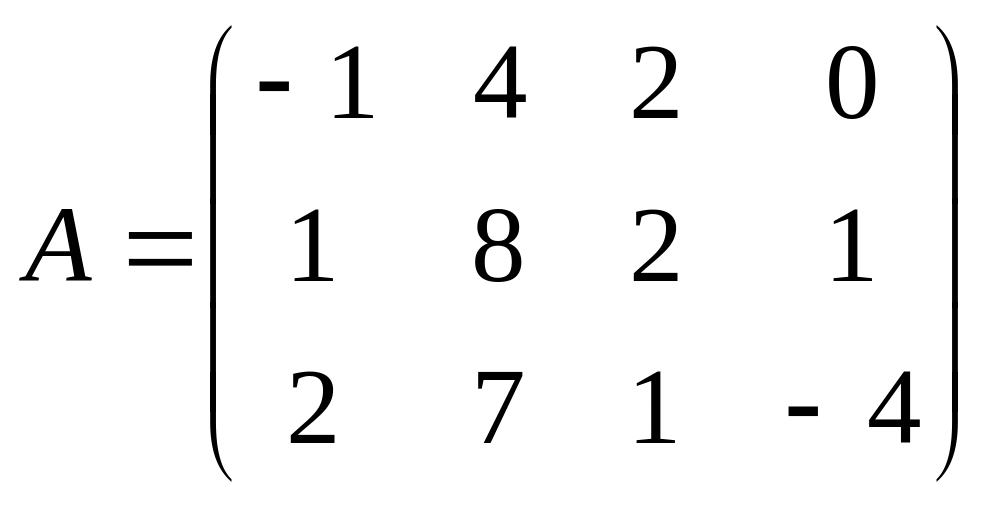
4 Задание. Исследовать на совместность, найти решение системы уравнений
а) методом Крамера;
б) с помощью обратной матрицы.
Сделайте проверку полученного решения.
5 Задание. Найти многочлен 3-ей степени f (x) , для которого
f (1) = −2 , f (−1) = −6 , f (−2) = −20 , f (3) =10.
6
Задание.
Докажите, что векторы
,
,
образуют
базис
и
найдите
разложение
вектора
по
векторам
,
,
если
,
,
,
.
7 Задание Сельскохозяйственное предприятие засевает пятью культурами площади 200 , 120 , 230, 160 , 180 га соответственно. Урожайности культур равны 12 , 13 , 16 , 26 , ? ц/га. Составить вектор площадей и урожайностей культур, определить общий сбор культур, определите количество дней, необходимых для обработки площади под каждой культурой, если обрабатывается 20 га в день
«?» - порядковый номер по журналу
8 Задание. В декартовой прямоугольной системе координат даны 3 точки:
А(3,0,1), В(1,3,0), С(4,-1,2).
Найдите:
а) длину отрезка АВ и координаты точки М – середины этого отрезка;
б) уравнение прямой АВ и прямой ВС;
в) угол между прямыми АВ и ВС;
г) уравнение плоскости АВС.