
- •Введение
- •1 Требования к выполнению и оформлению контрольных работ
- •2 Вопросы для подготовки к экзаменам
- •I семестр
- •II семестр
- •3 Содержание контрольных работ
- •4 Задания Контрольной работы № 1
- •5 Задания Контрольной работы № 2
- •6 Задания Контрольной работы № 3
- •7 Задания контрольной работы № 4
- •8 Задания контрольной работы № 5
- •Библиографический список
4 Задания Контрольной работы № 1
Задание 1.1.
Решить матричное уравнение АХ=В, если:
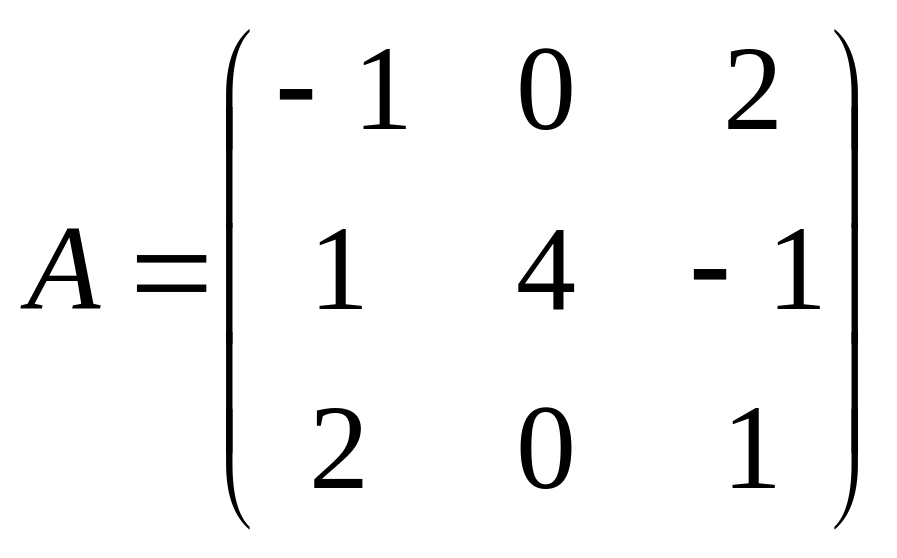 ,
,
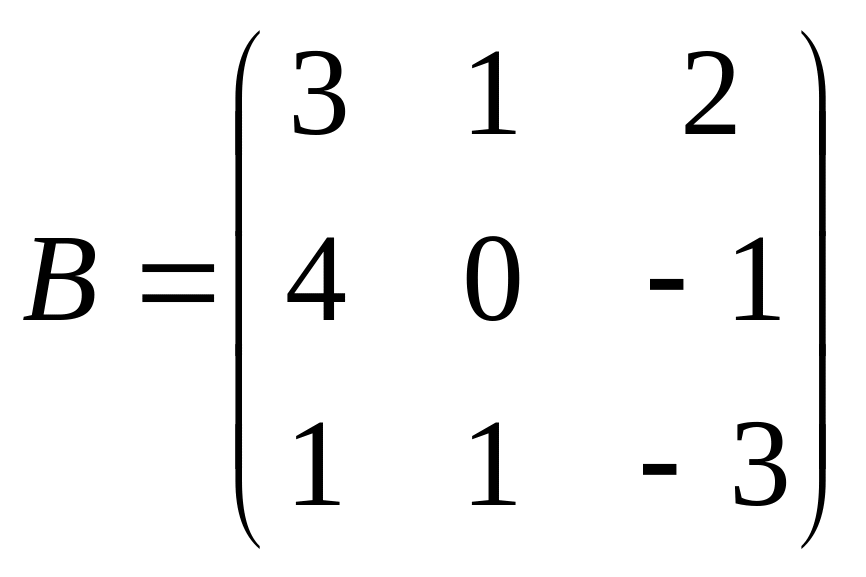 .
. ,
,
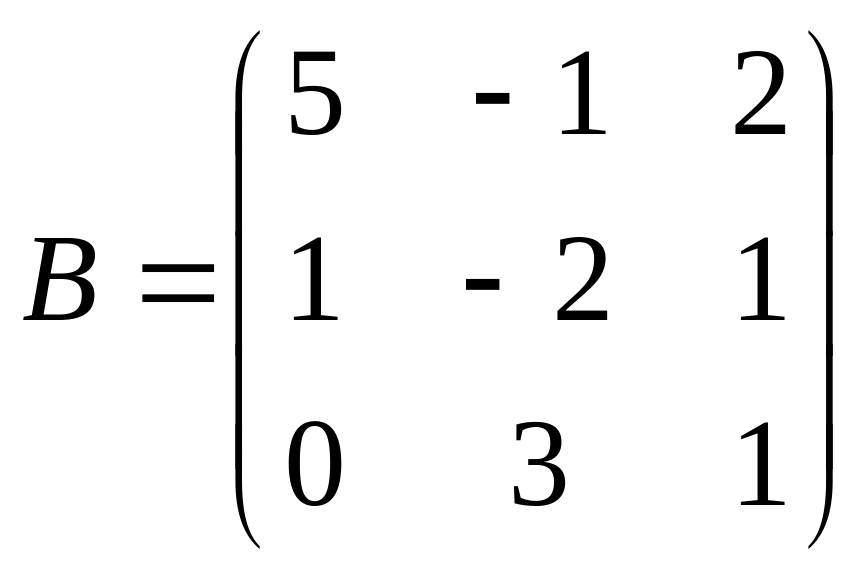 .
.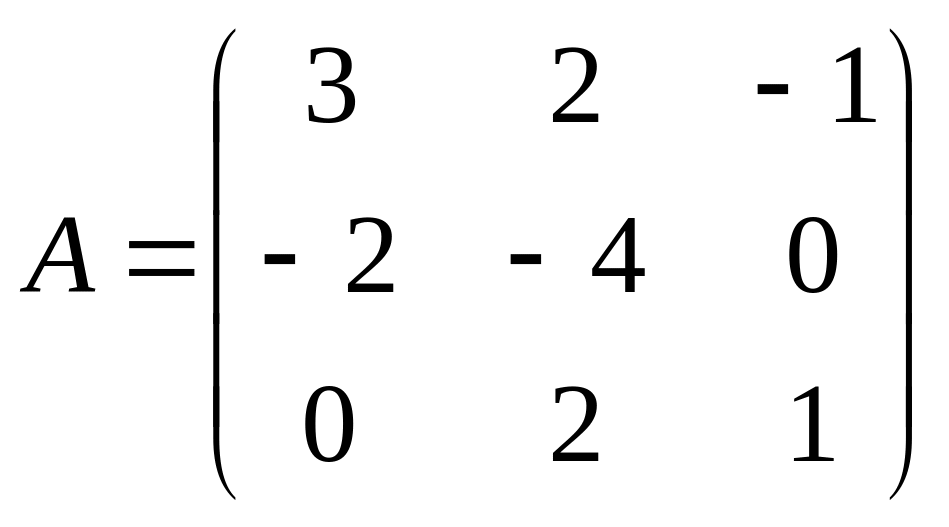 ,
,
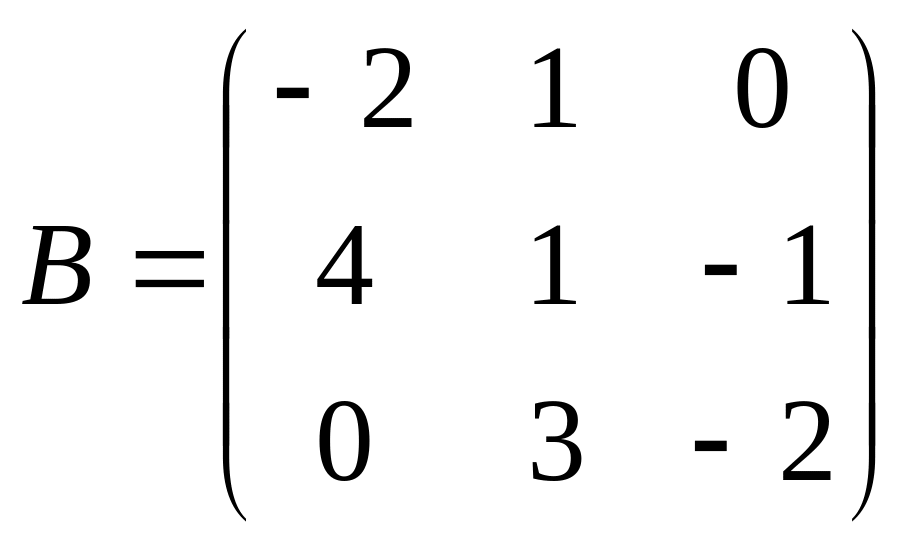 .
.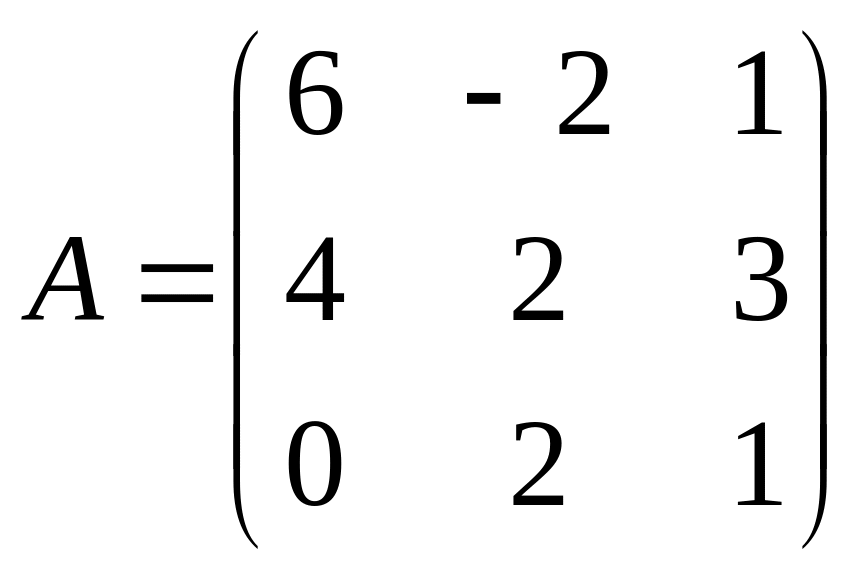 ,
,
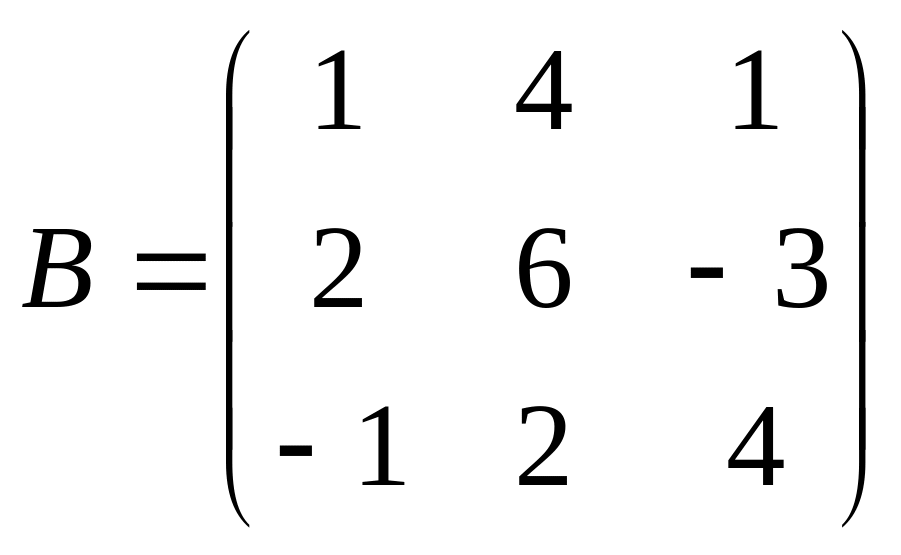 .
.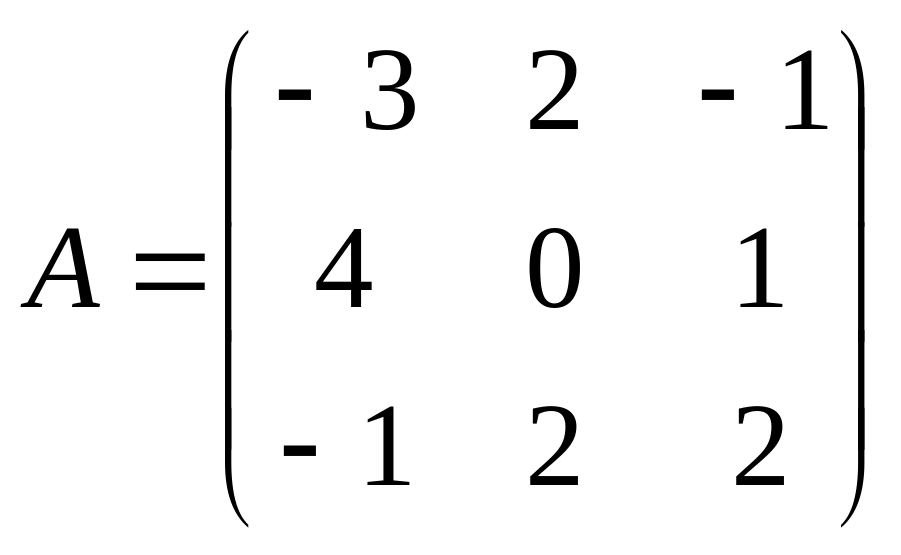 ,
,
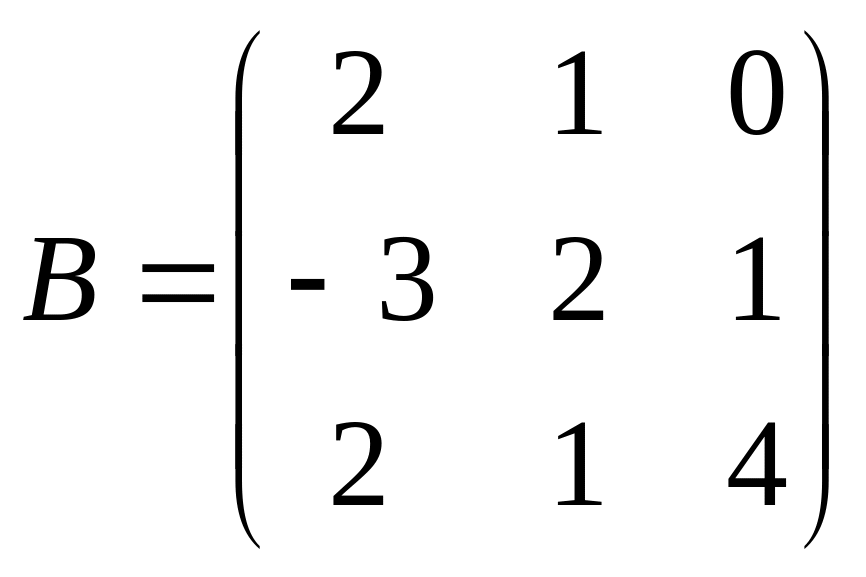 .
.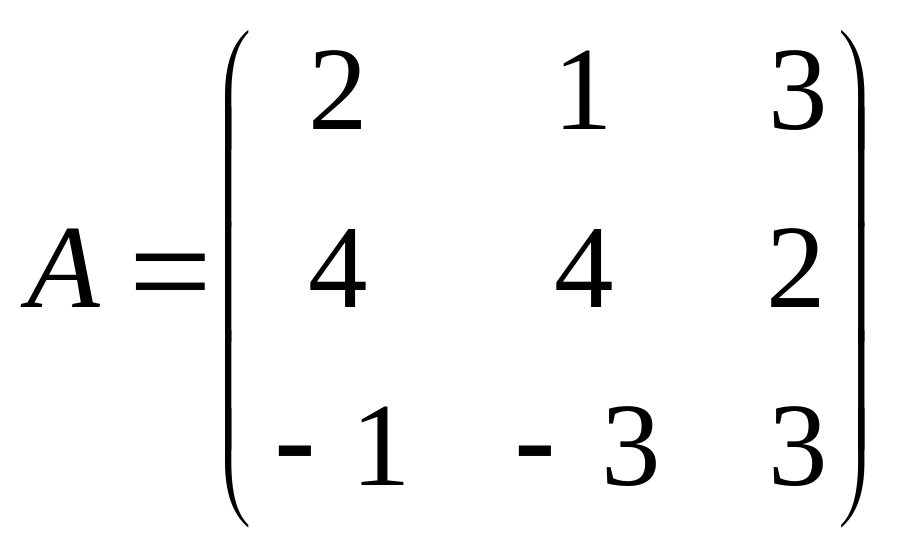 ,
,
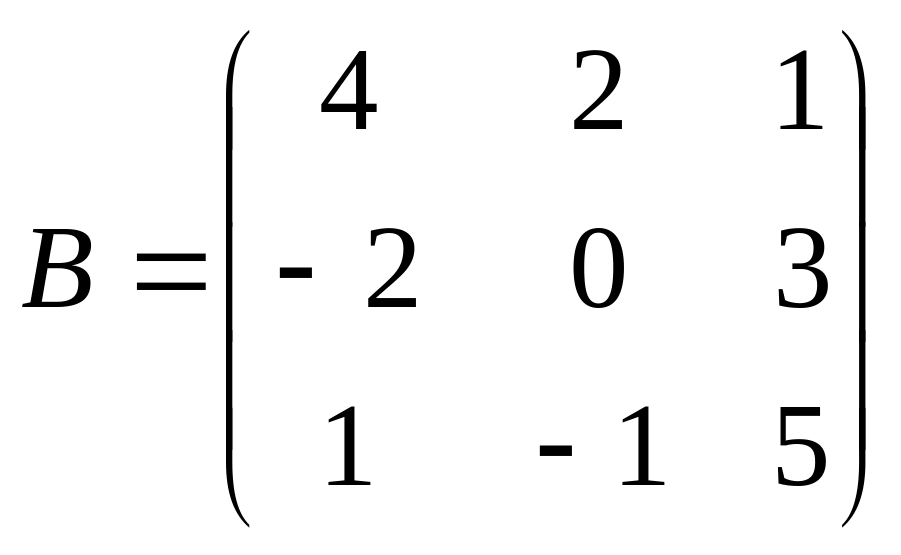 .
.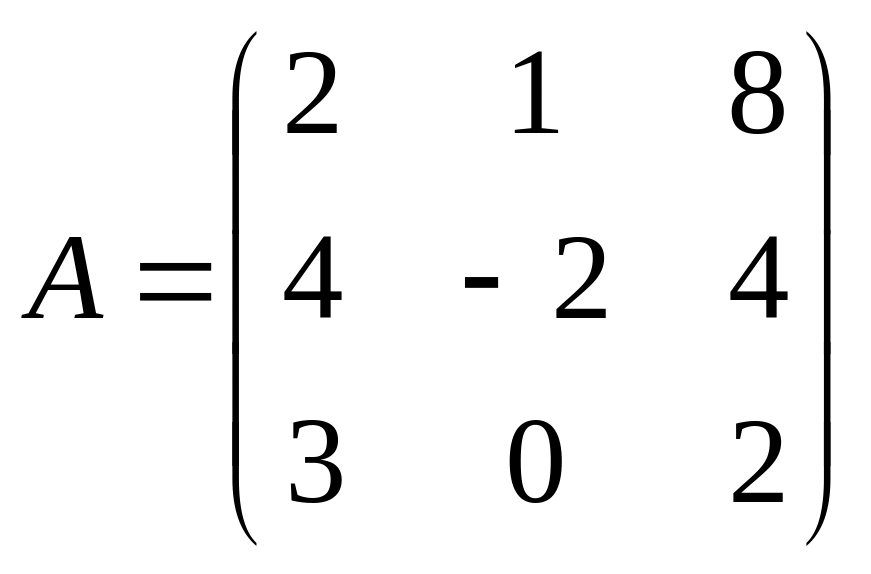 ,
,
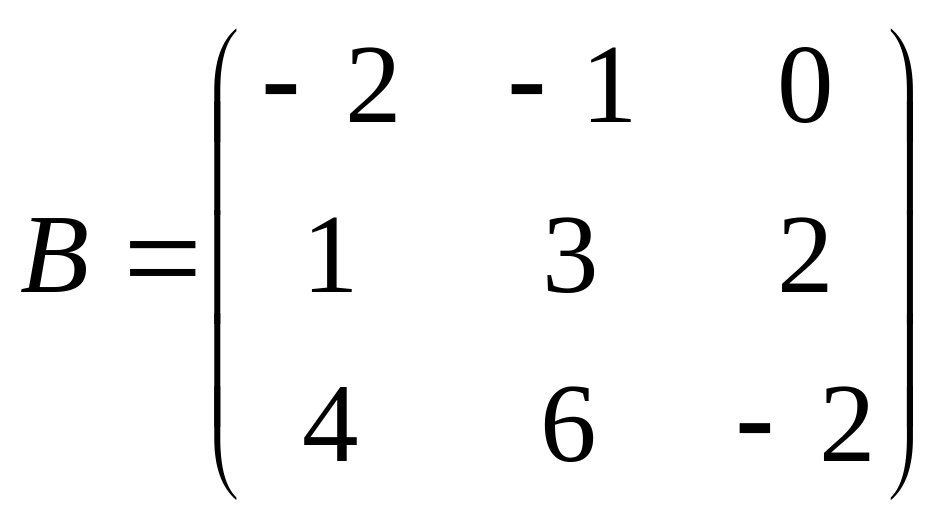 .
.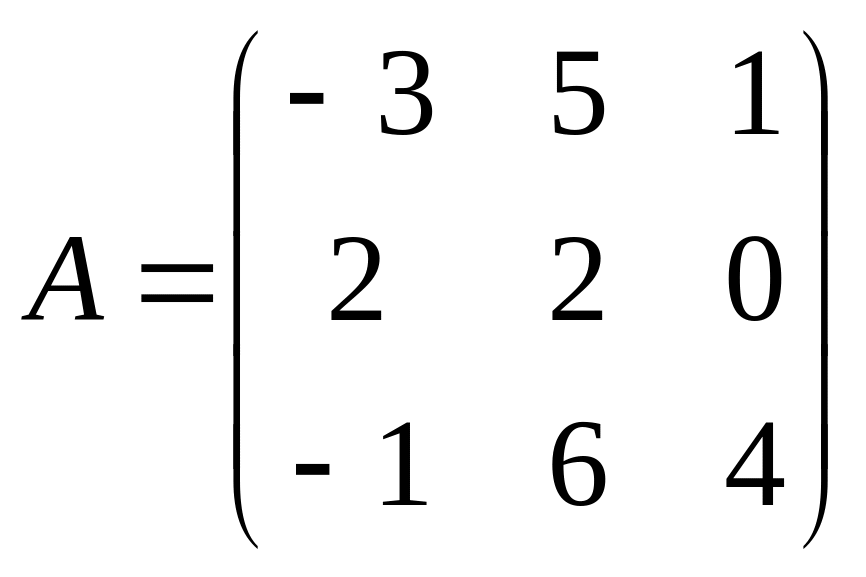 ,
,
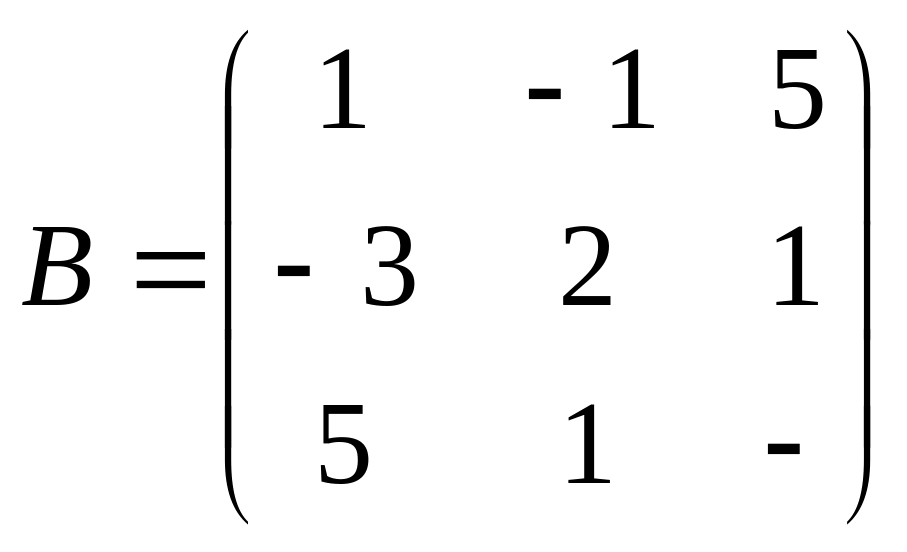 .
.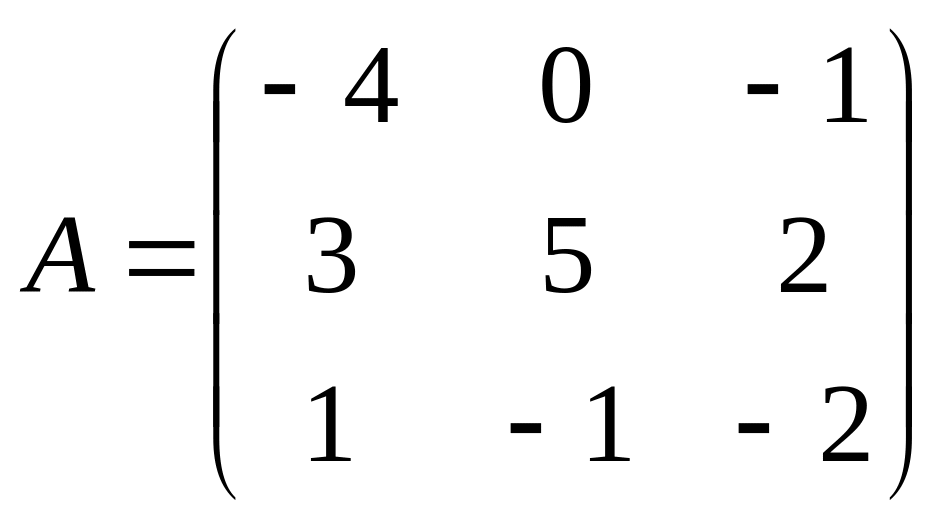 ,
,
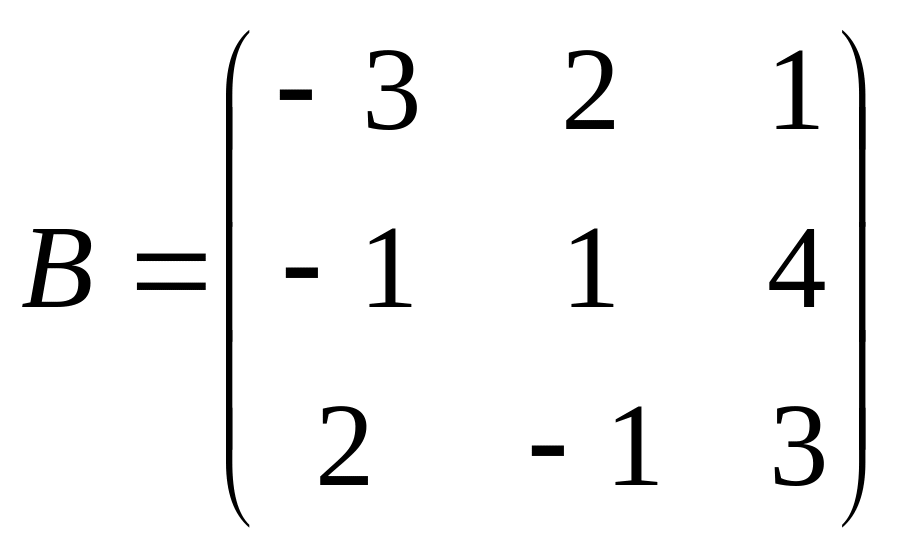 .
.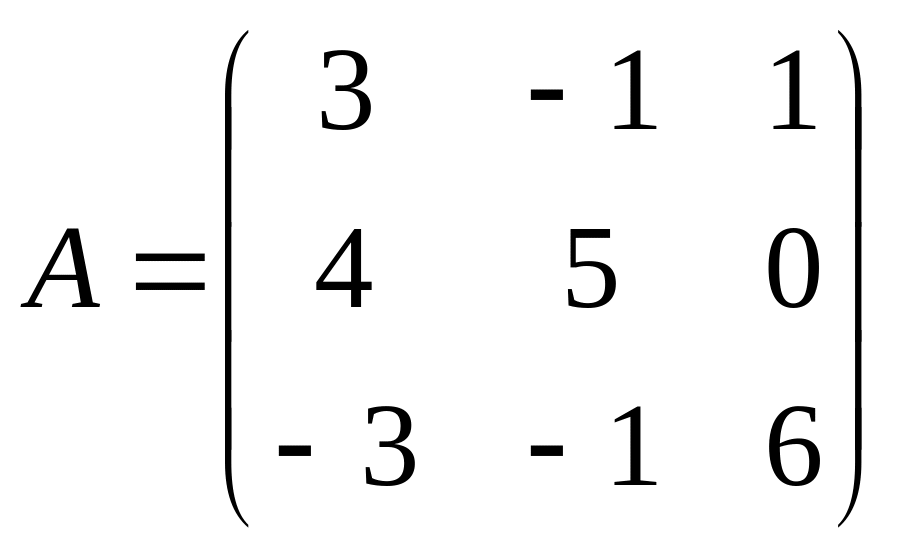 ,
,
 .
.
Задание 1.2.
Найти все решения системы линейных уравнений:
а) по формулам Крамера;
б) методом Гаусса.
-
а)
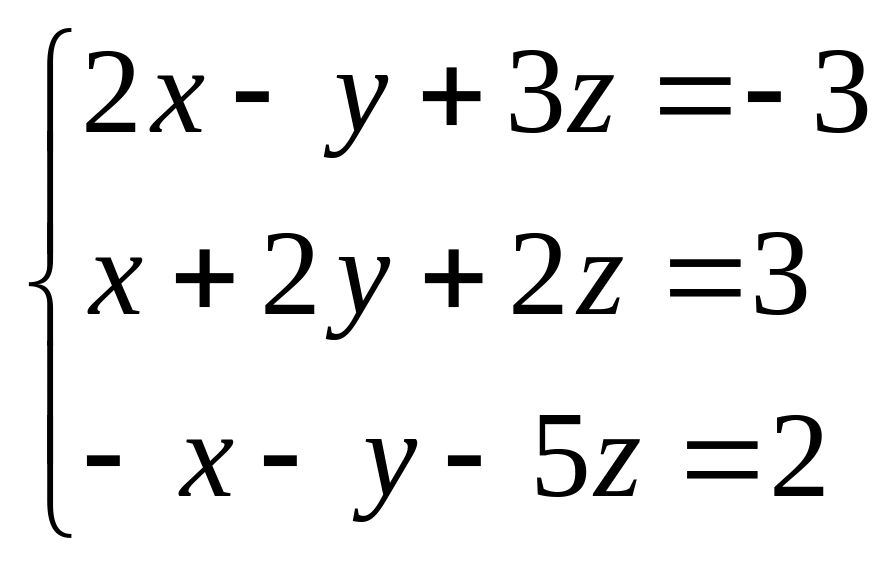
б)
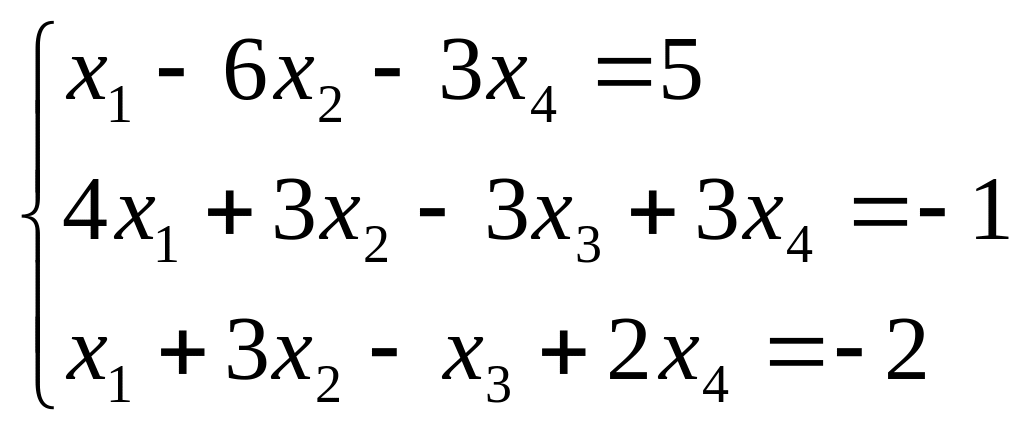
а)
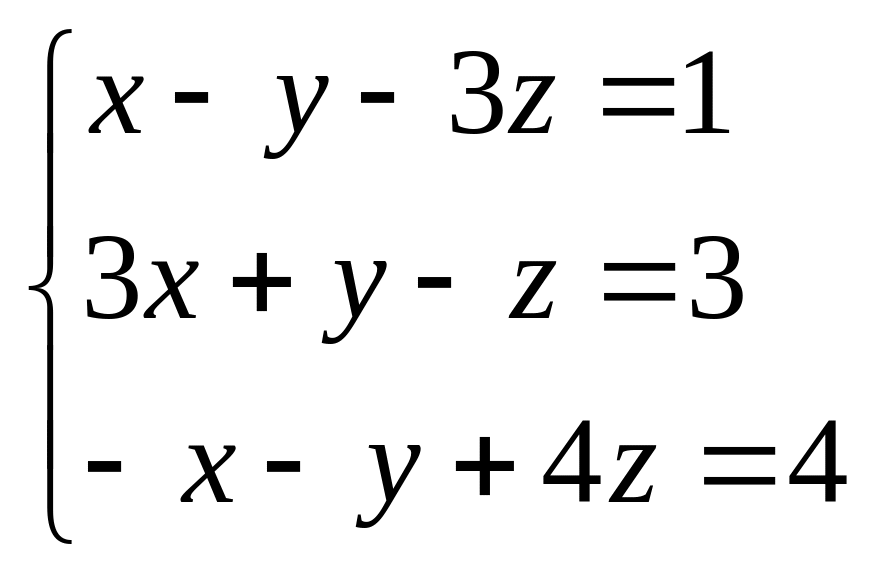
б)
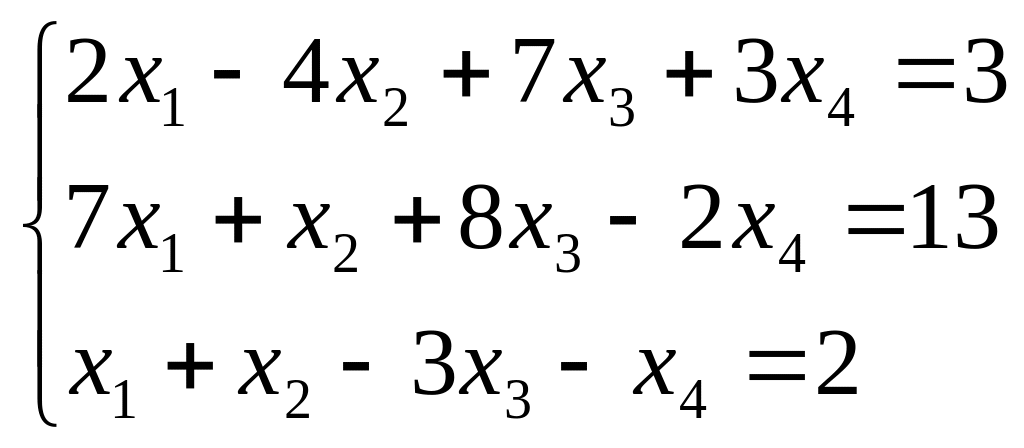
а)
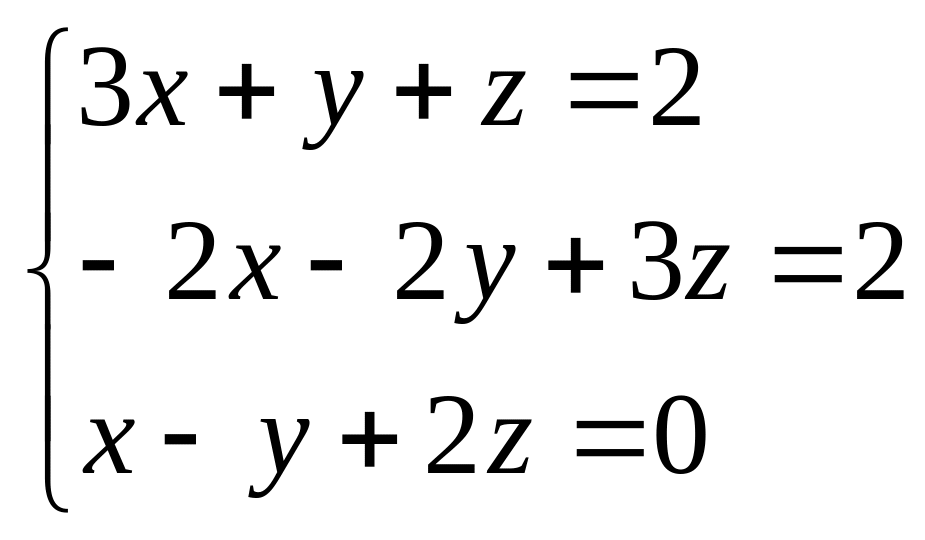
б)
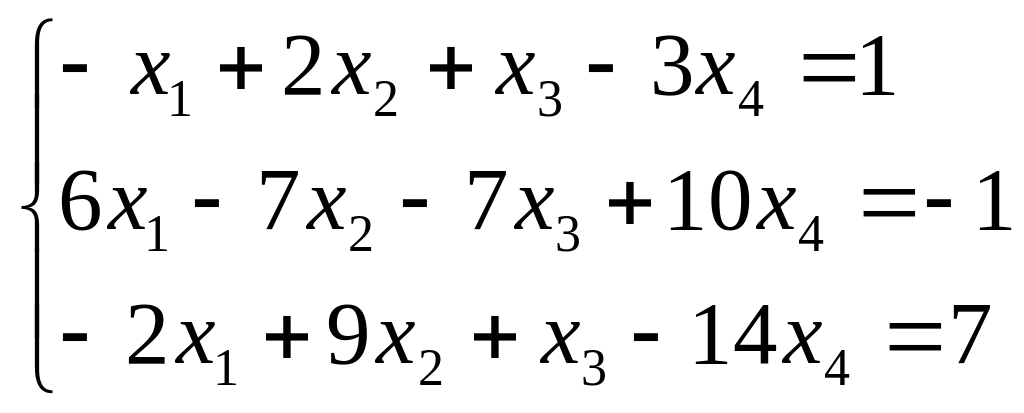
а)
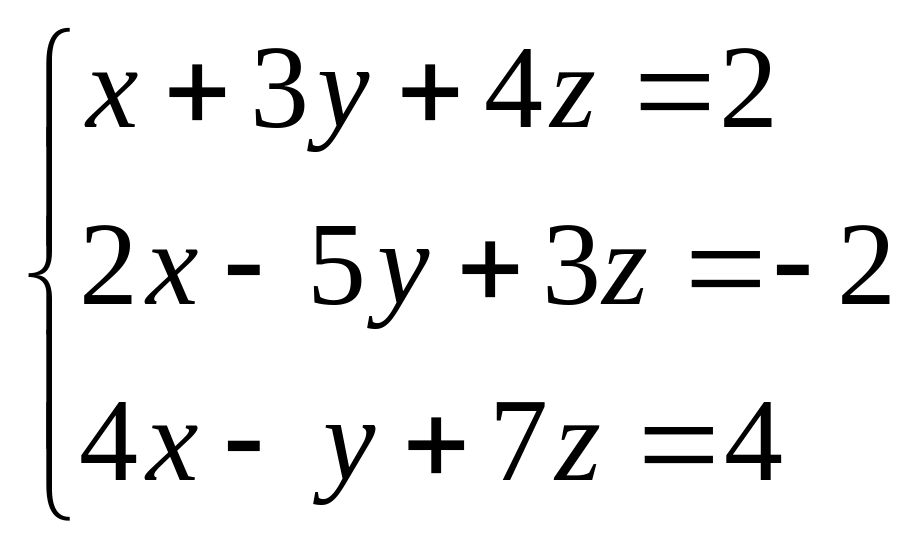
б)
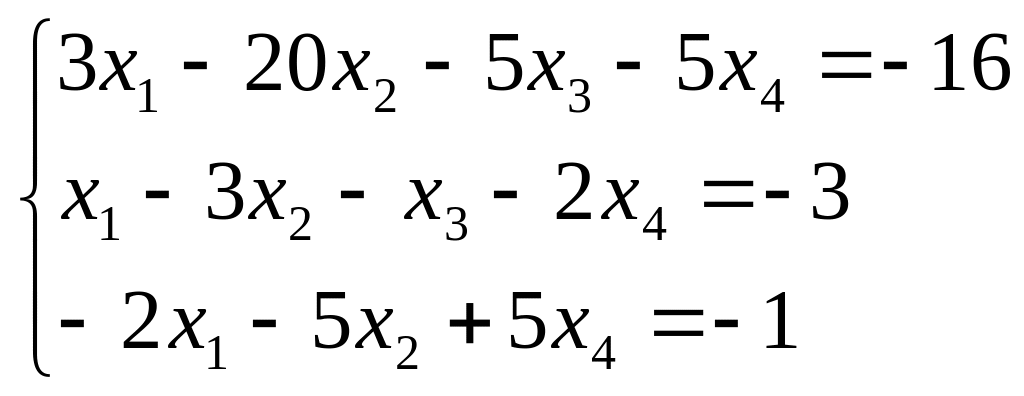
а)
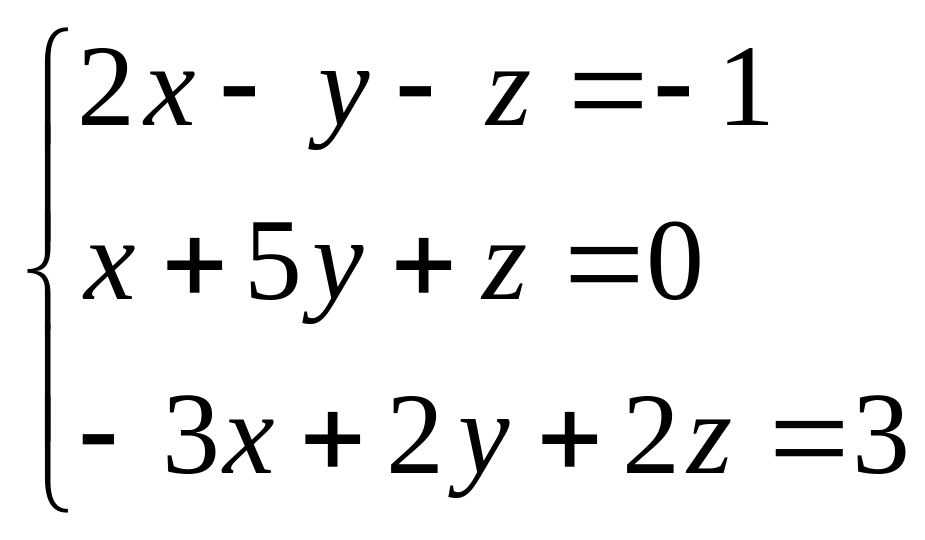
б)
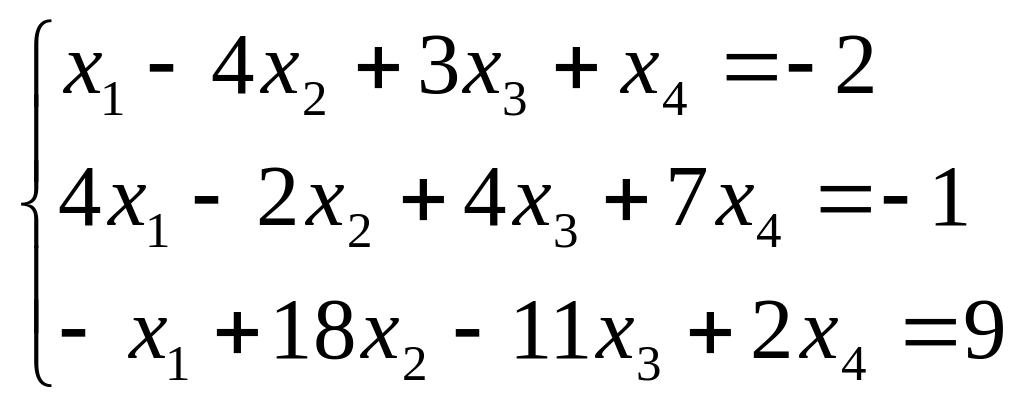
а)
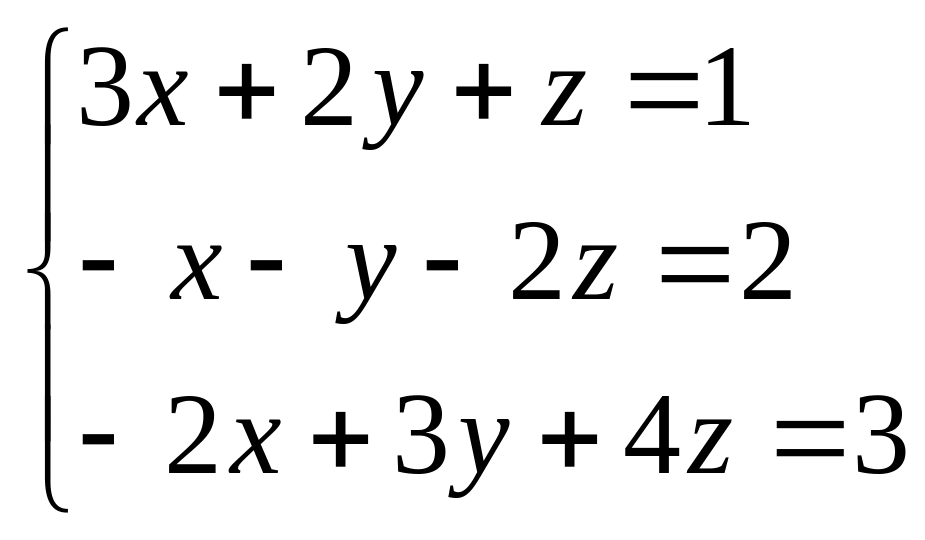
б)
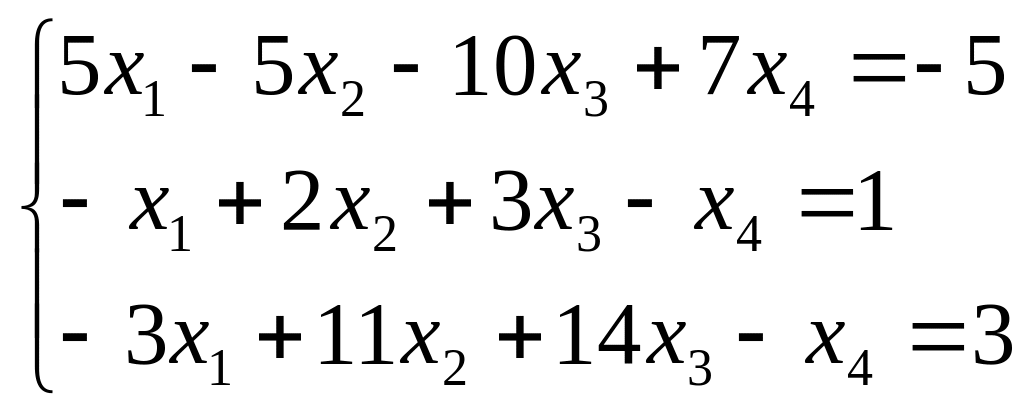
а)
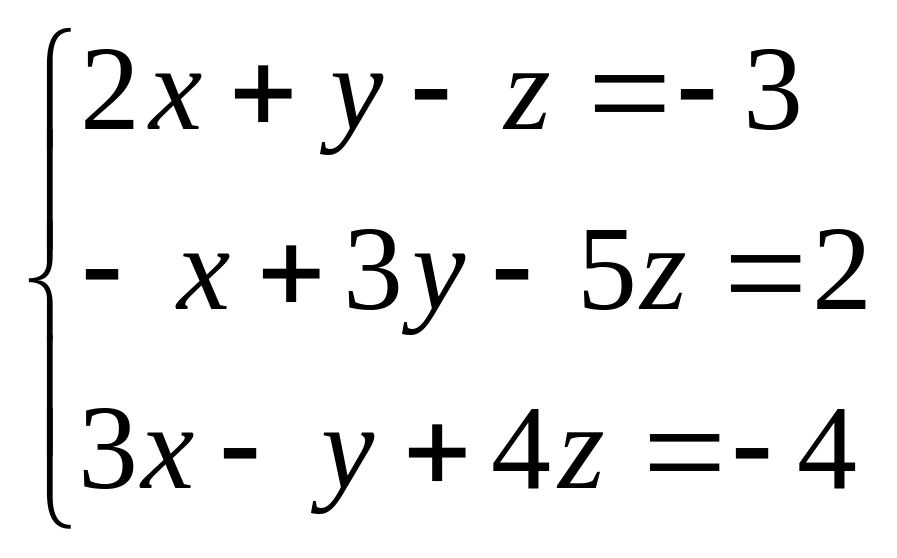
б)

а)
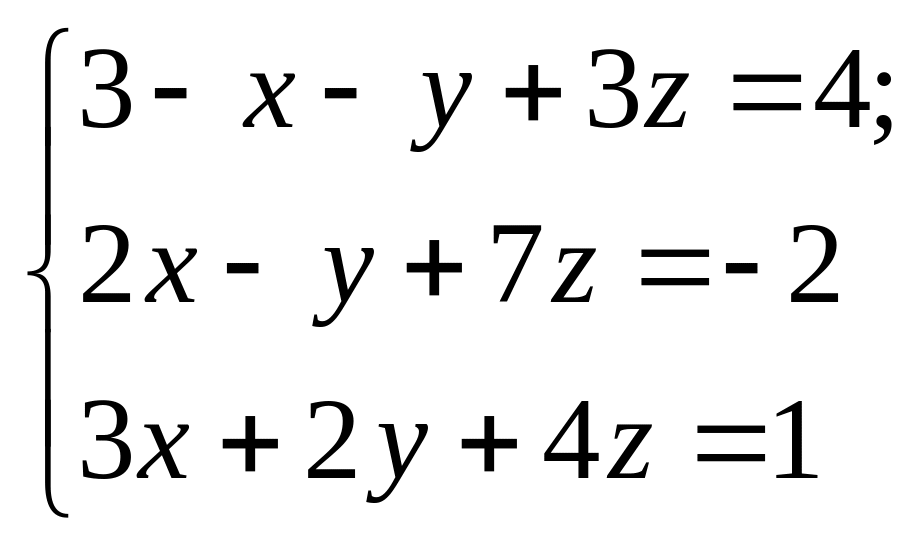
б)
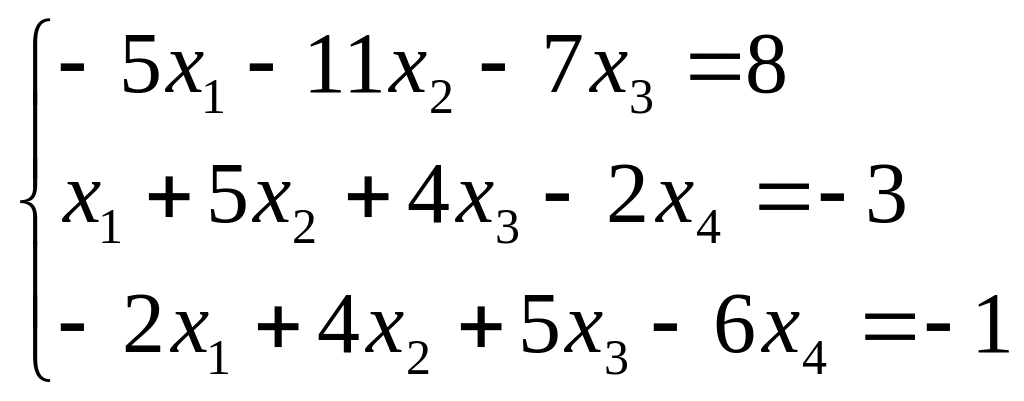
а)
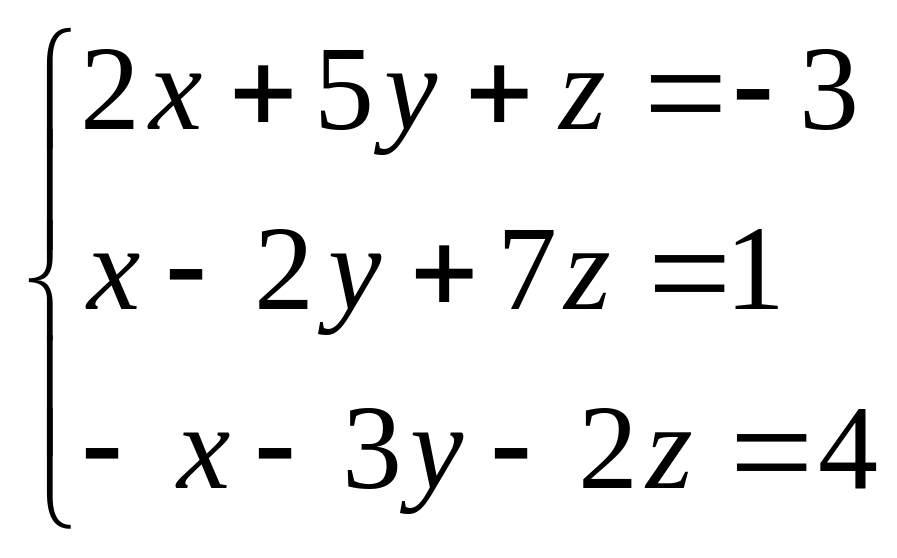
б)
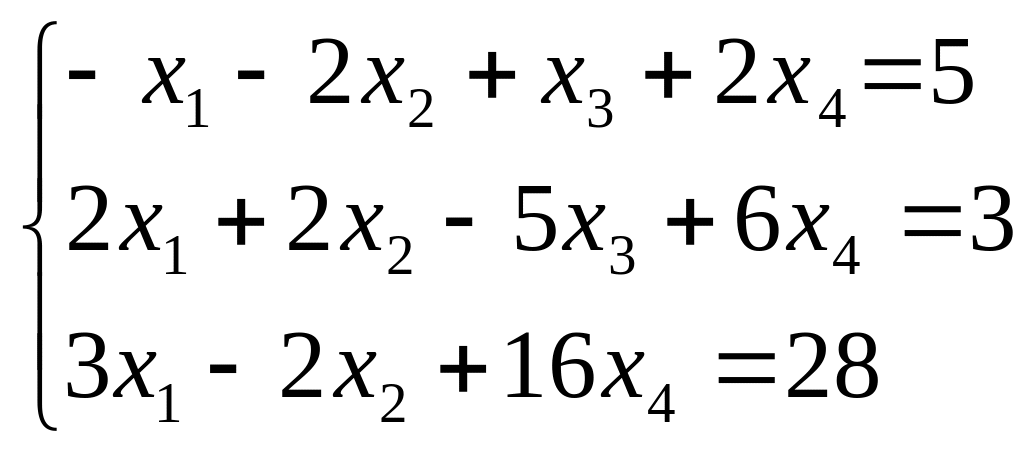
а)
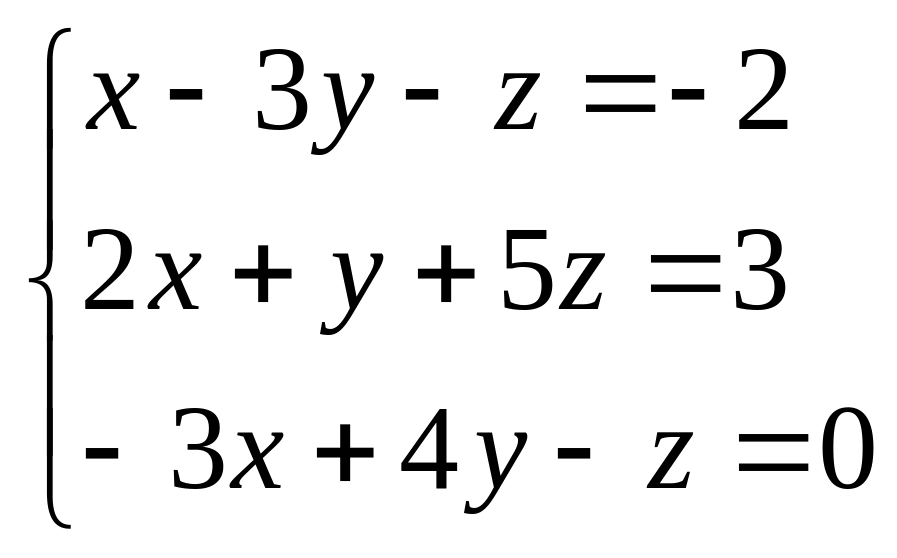
б)
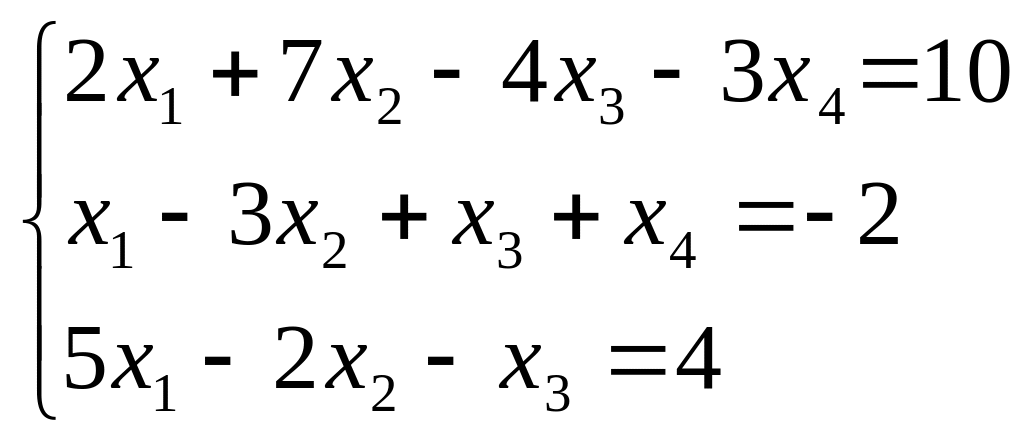
Задание 1.3. Даны вершины треугольника АВС. Найти:
а) длины сторон треугольника;
б) тангенс угла между высотой ВН и медианой ВМ треугольника, проведенных из одной вершины;
в) длину высоты ВН;
г) площадь треугольника.
А(4;2), В(2;-5), С(-5;-1);
А(-3;-4), В(2;6), С(7;-2);
А(-2;-7), В(-4;-1), С(4;2);
А(-3;3), В(5;5), С(0;-3);
А(-2;-3), В(0;5), С(7;3);
А(-4;3), В(6;4), С(2;-8);
А(4;-1), В(-4;5), С(5;8);
А(1;6), В(2;-3), С(-5;-2);
А(2;6), В(-1;-4), С(-5;-1);
А(7;0), В(-2;-4), С(-5;5);
Задание 1.4.
Пирамида ABCD задана координатами вершин.
1)Найти угол между
векторами
![]() и
и
![]() .
.
2)Найти площадь основания ABC.
3)Найти объём пирамиды.
4) Составить уравнение плоскости ABC.
5) Составить канонические уравнения прямой, проходящей через высоту DH.
6)Найти длину высоты DH.
5 Задания Контрольной работы № 2
Задание 2.1.
Вычислить пределы.
-
а)
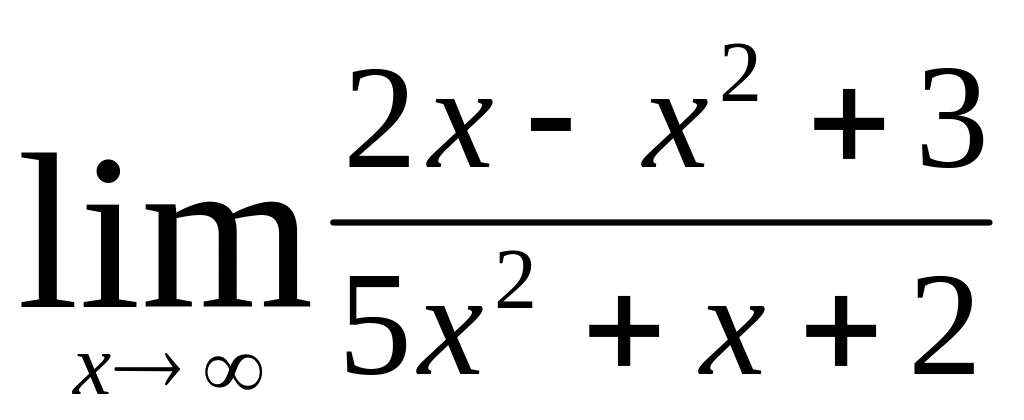 ;
;б)
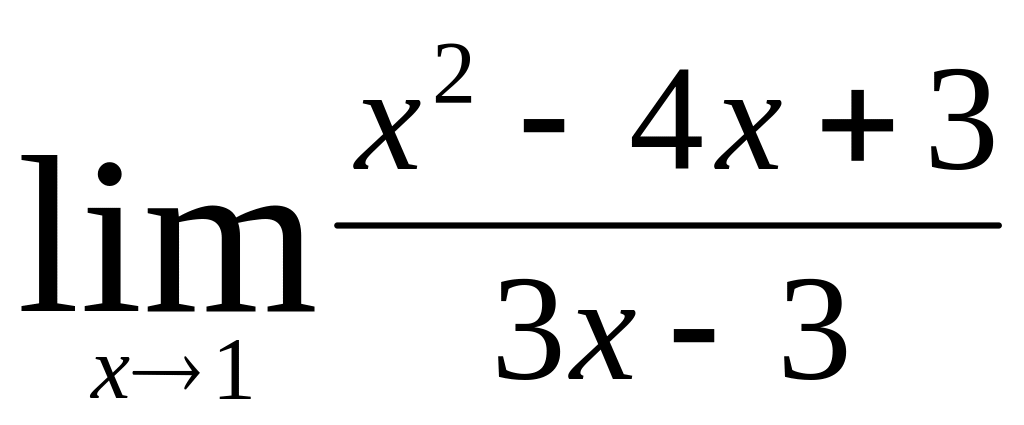 ;
;в)
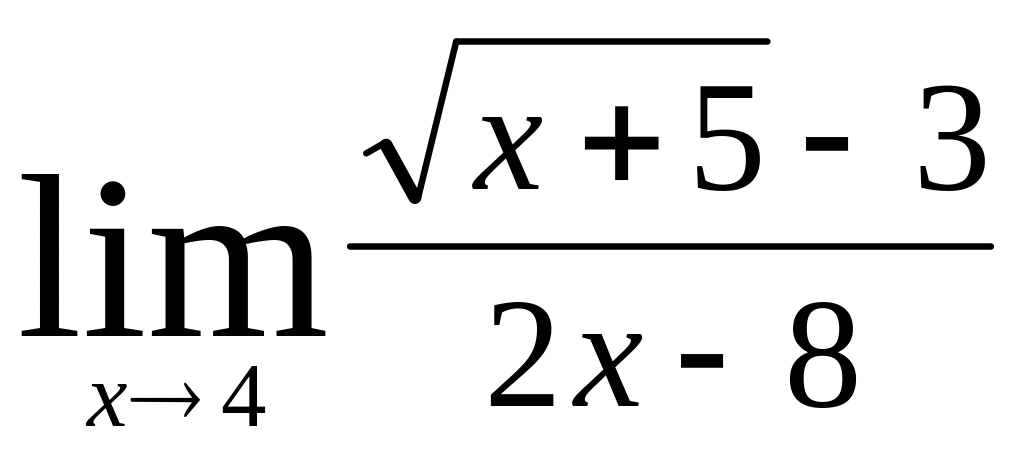 ;
;г)
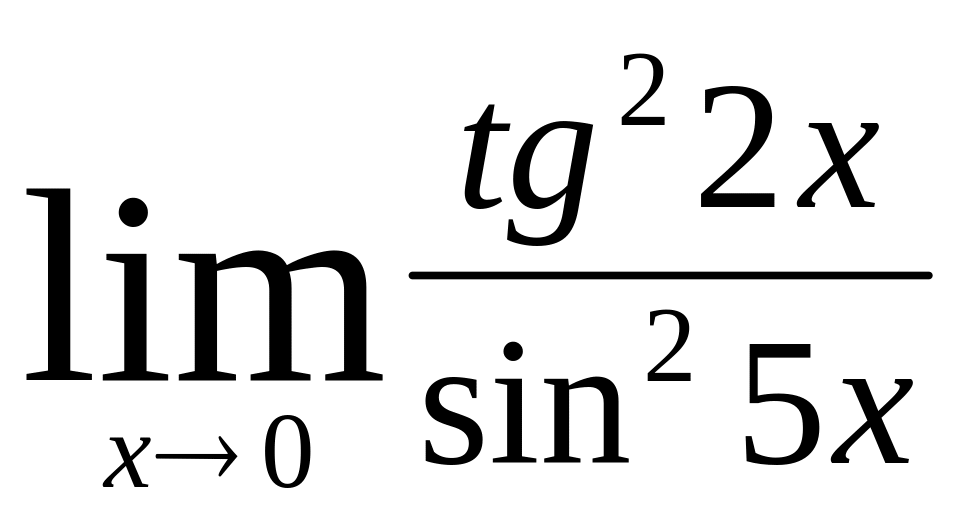 .
.а)
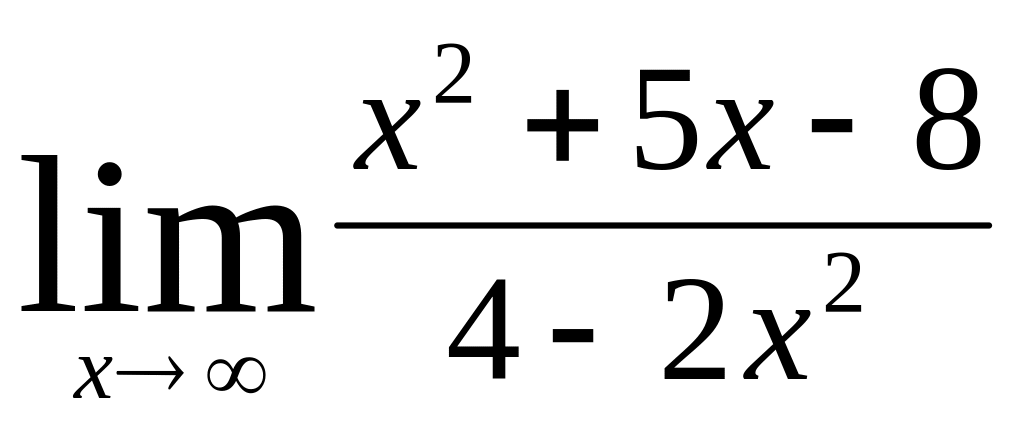 ;
;б)
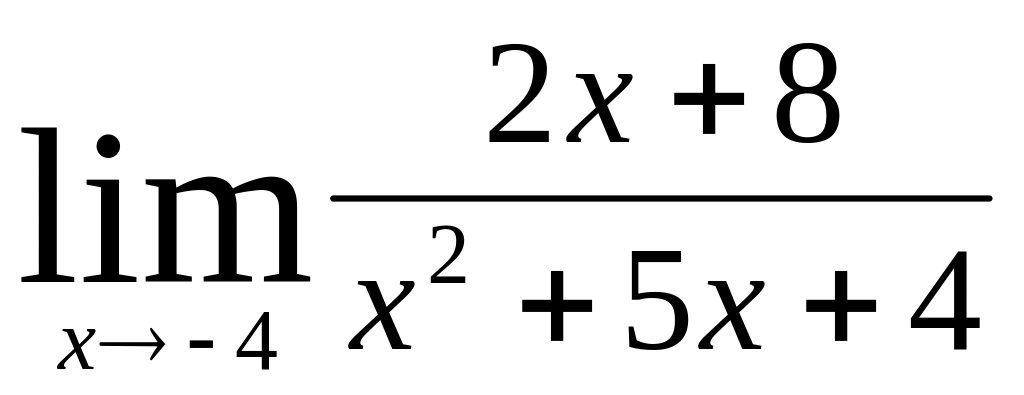 ;
;в)
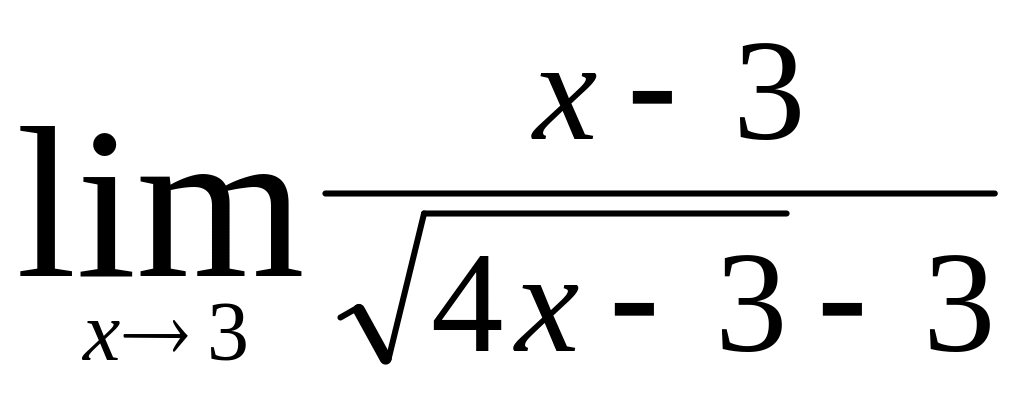 ;
;г)
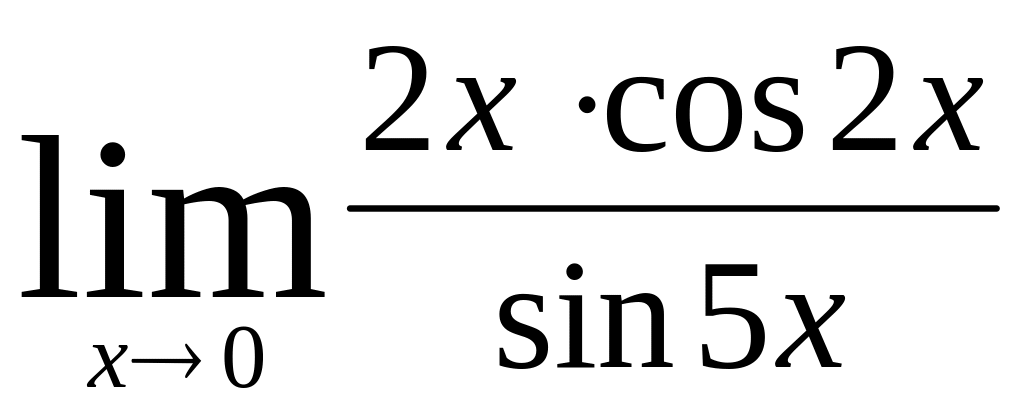 .
.а)
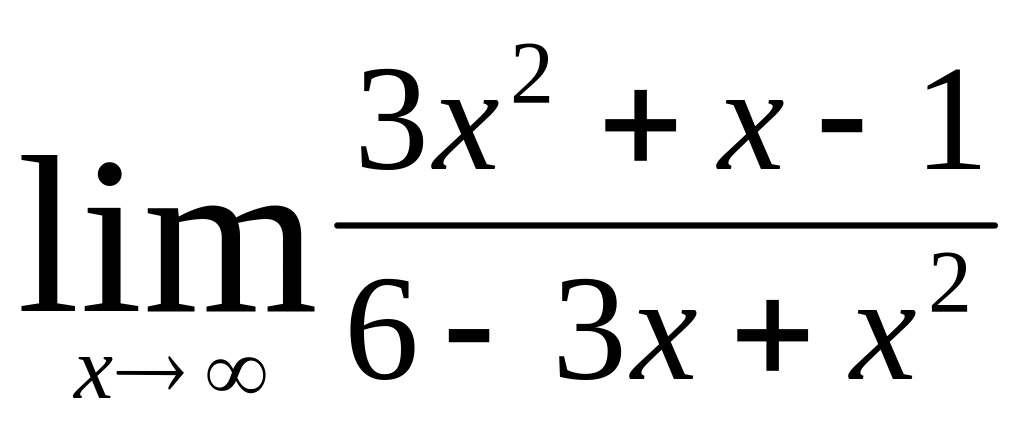 ;
;б)
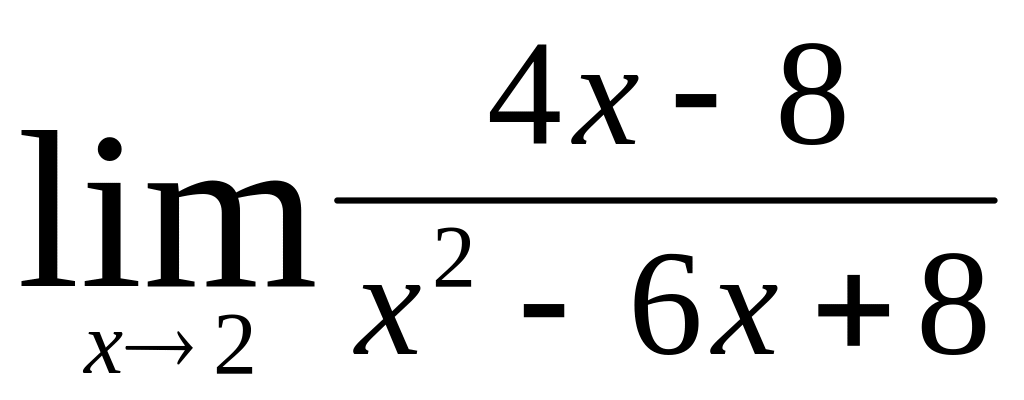 ;
;в)
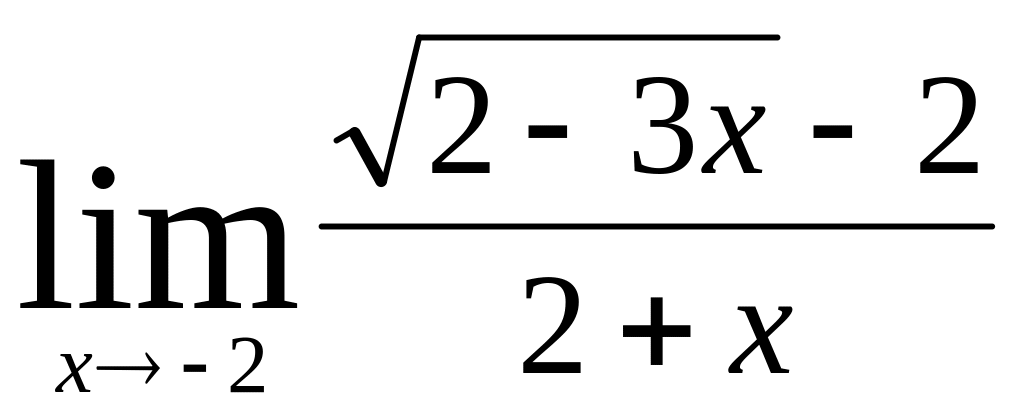 ;
;г)
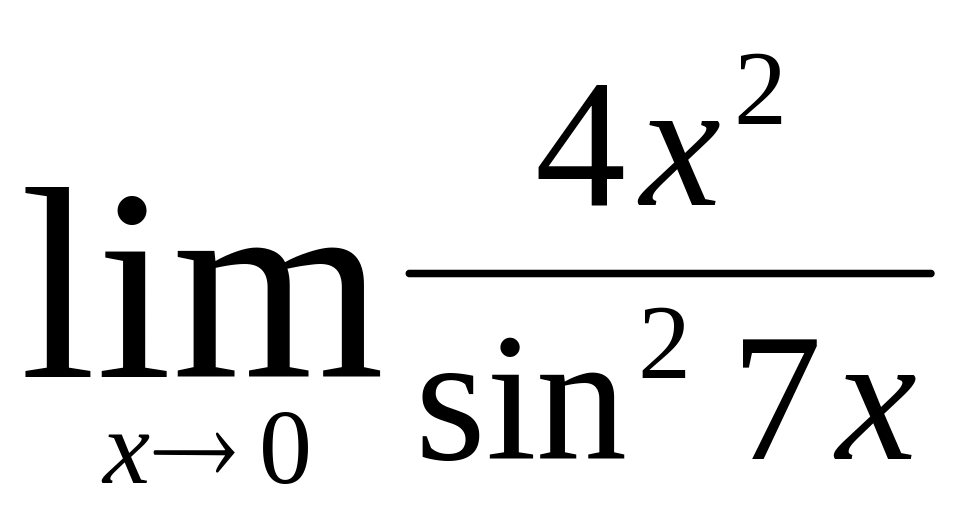 .
.а)
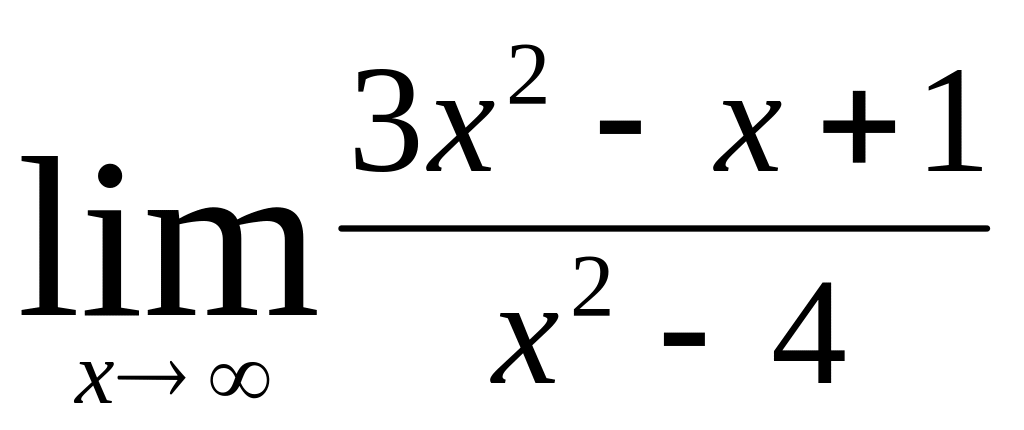 ;
;б)
 ;
;в)
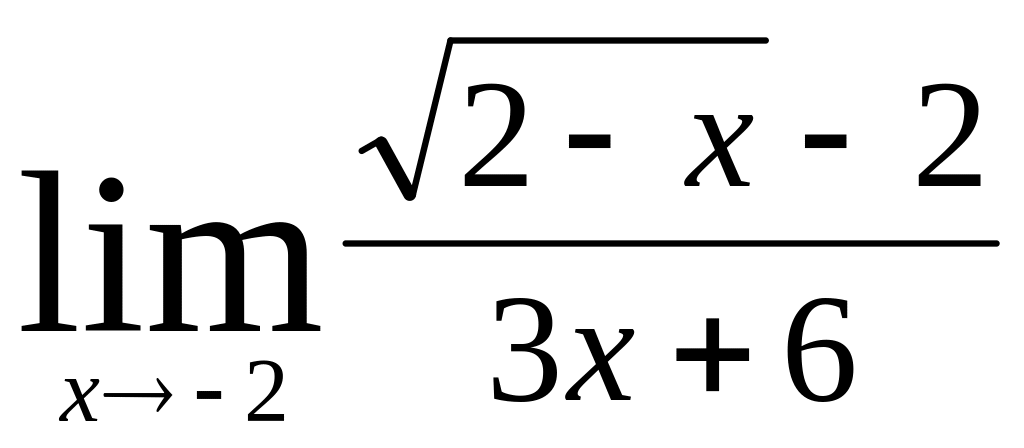 ;
;г)
 .
.а)
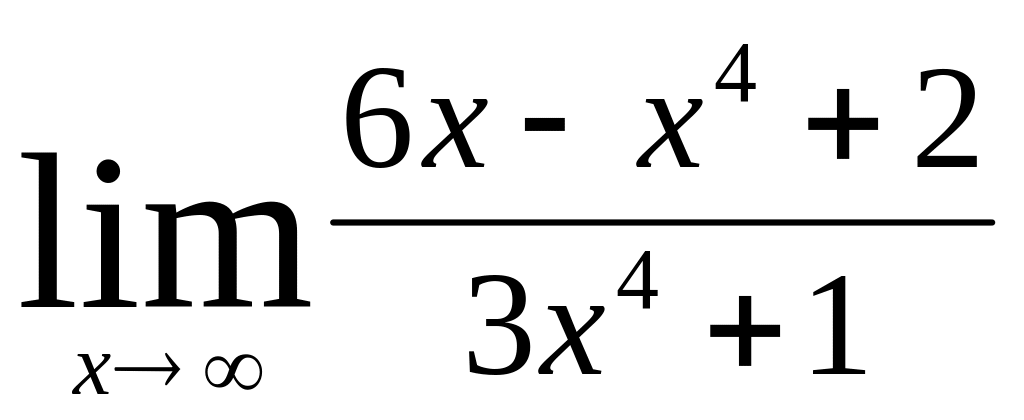 ;
;б)
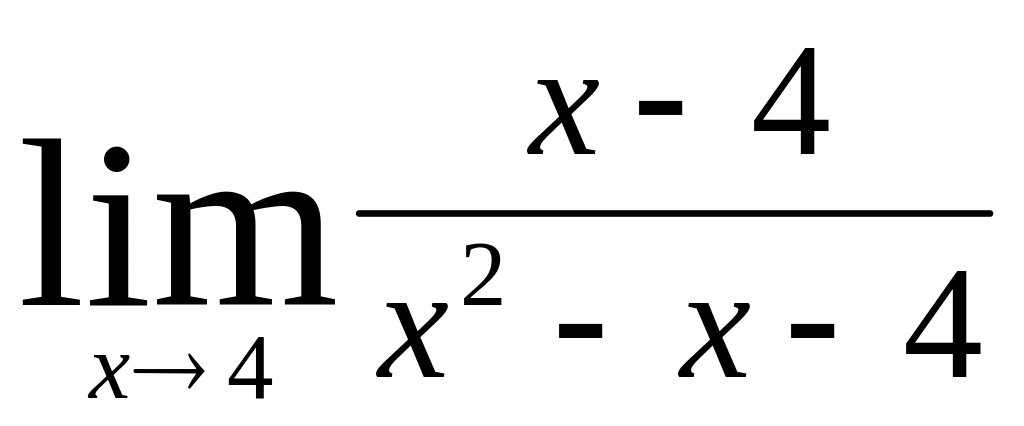 ;
;в)
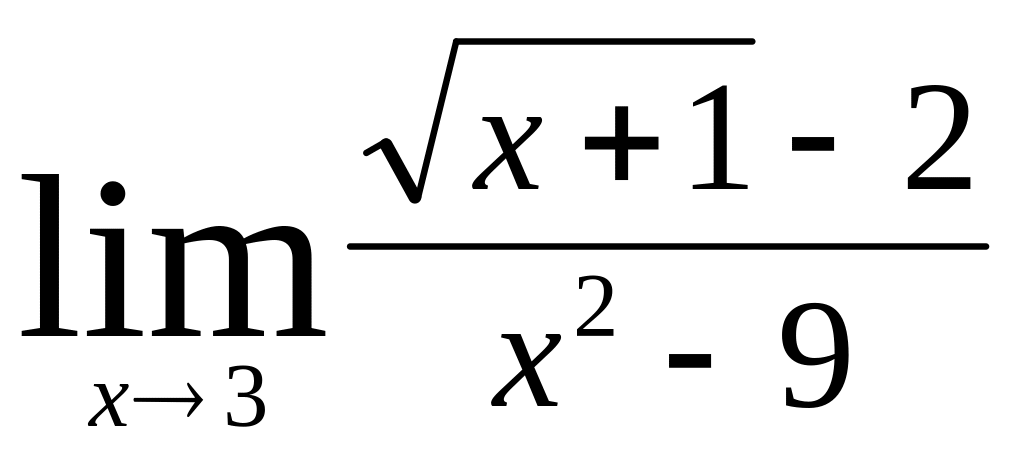 ;
;г)
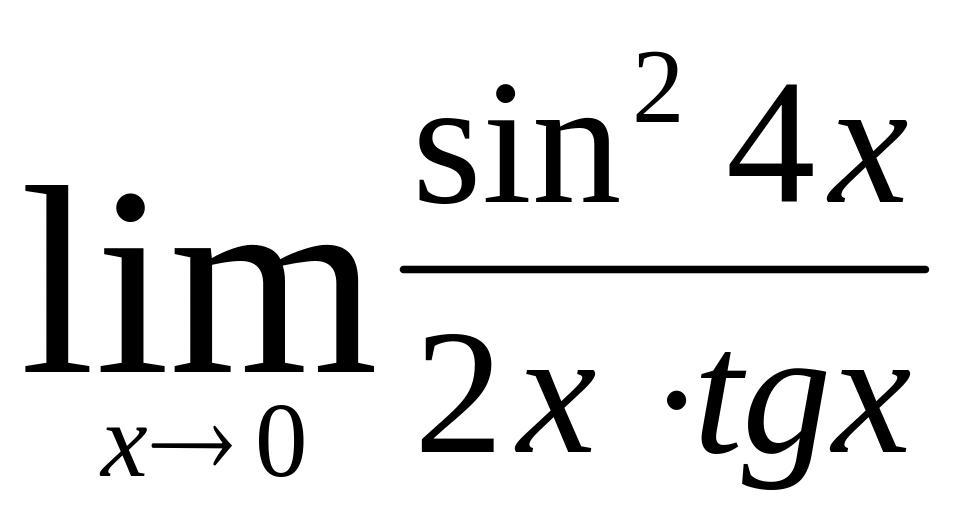 .
.а)
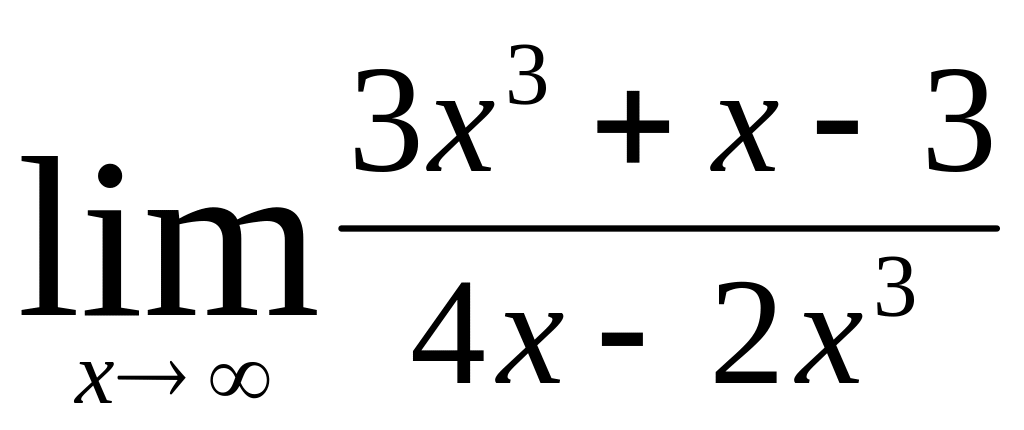 ;
;б)
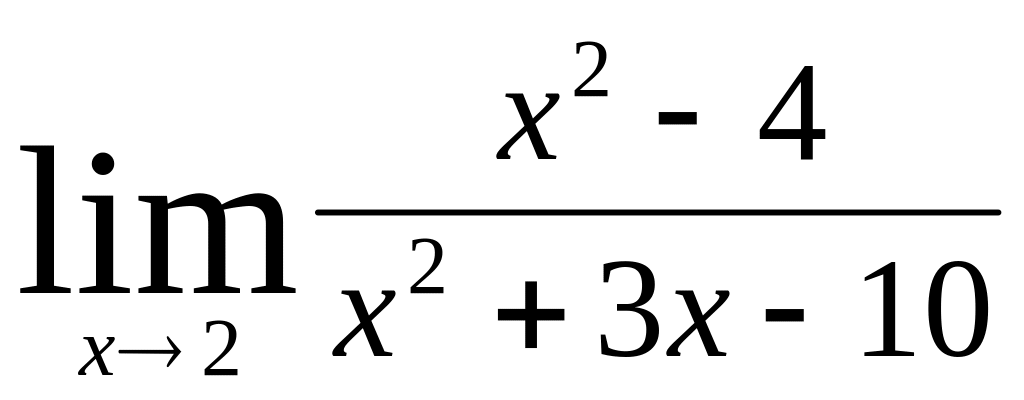 ;
;в)
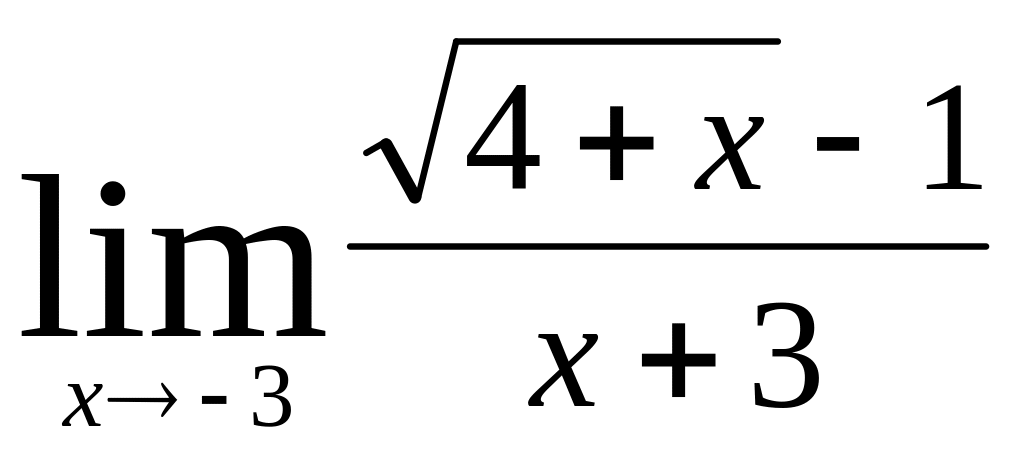 ;
;г)
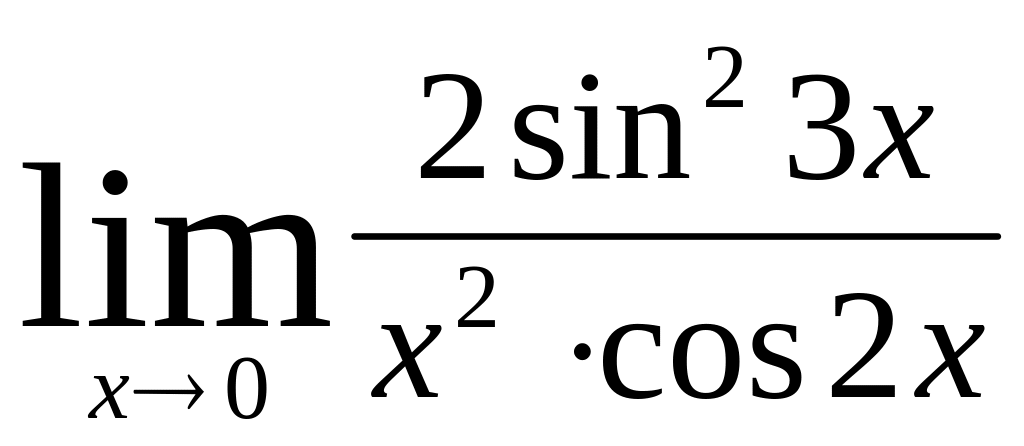 .
.а)
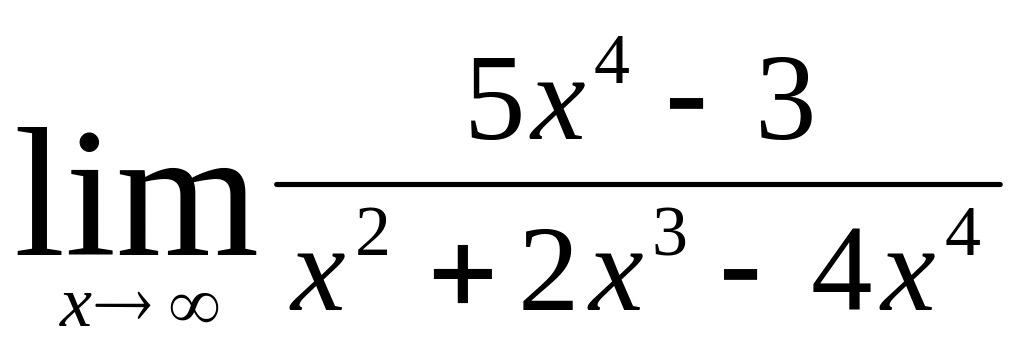 ;
;б)
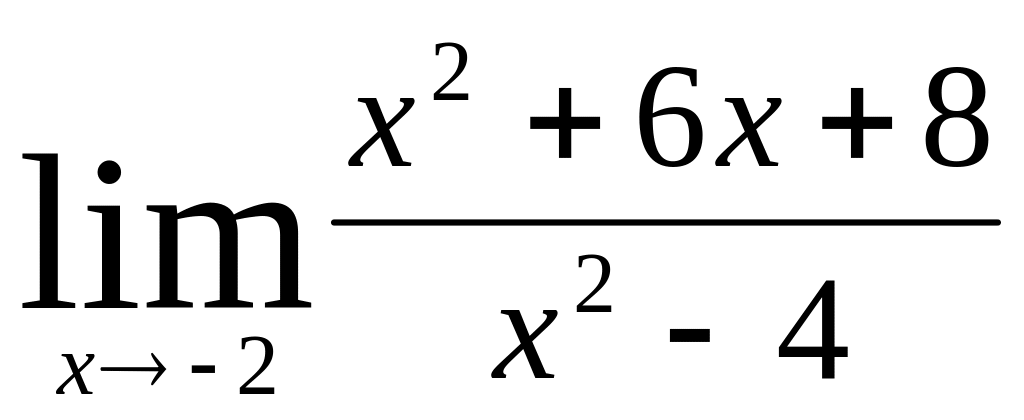 ;
;в)
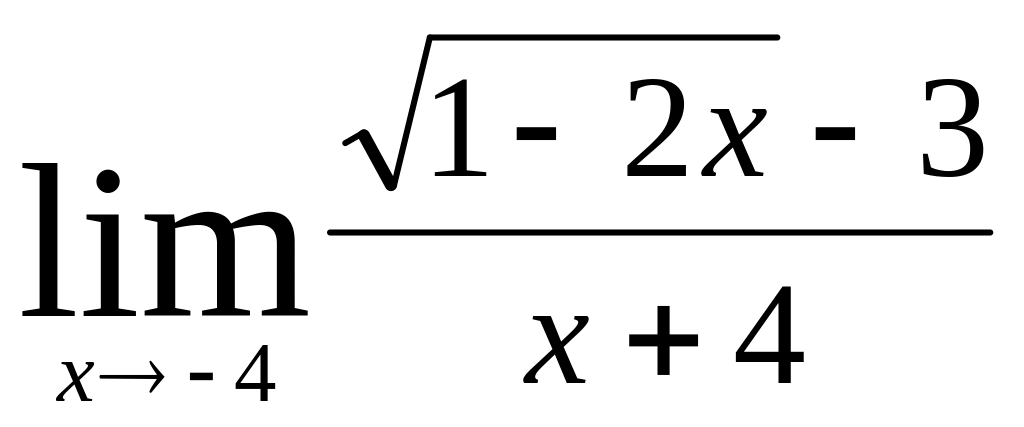 ;
;г)
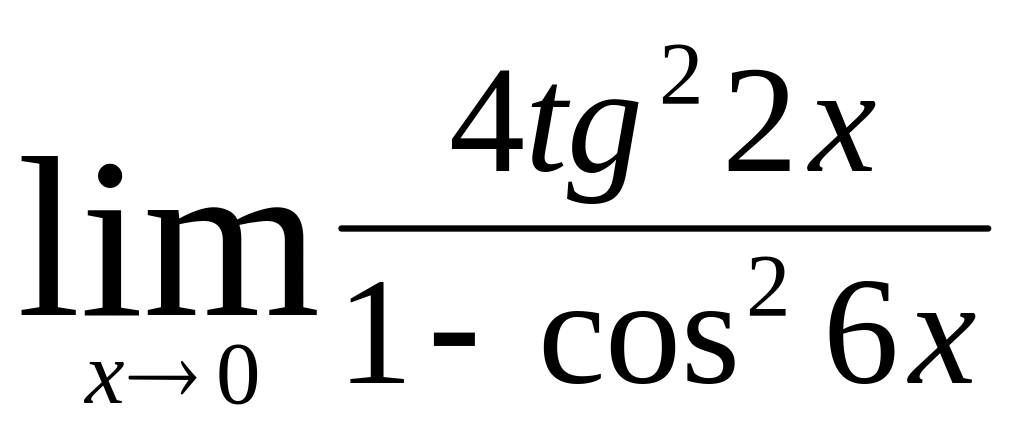 .
.а)
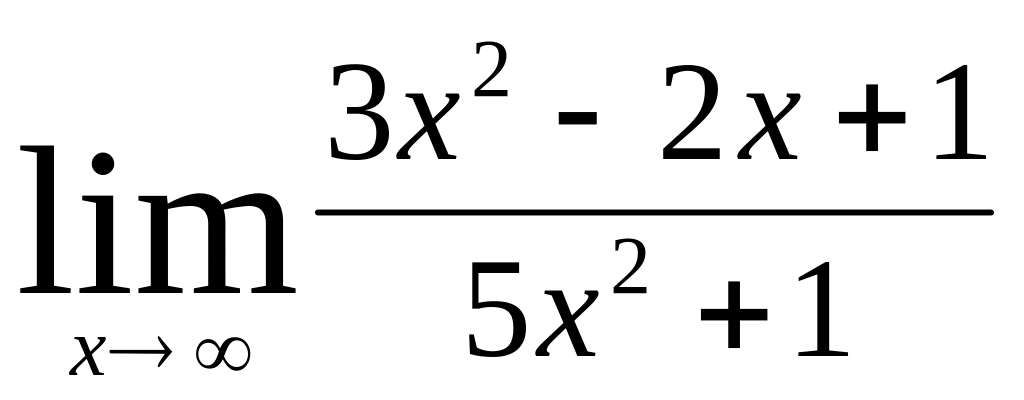 ;
;б)
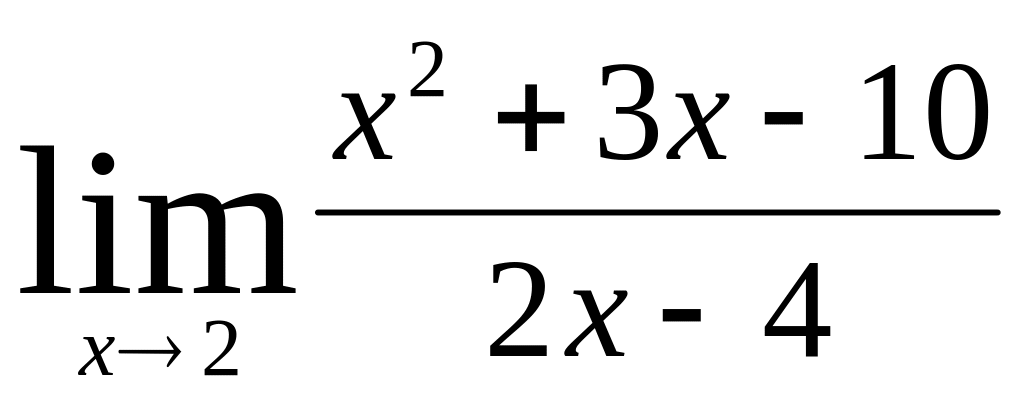 ;
;в)
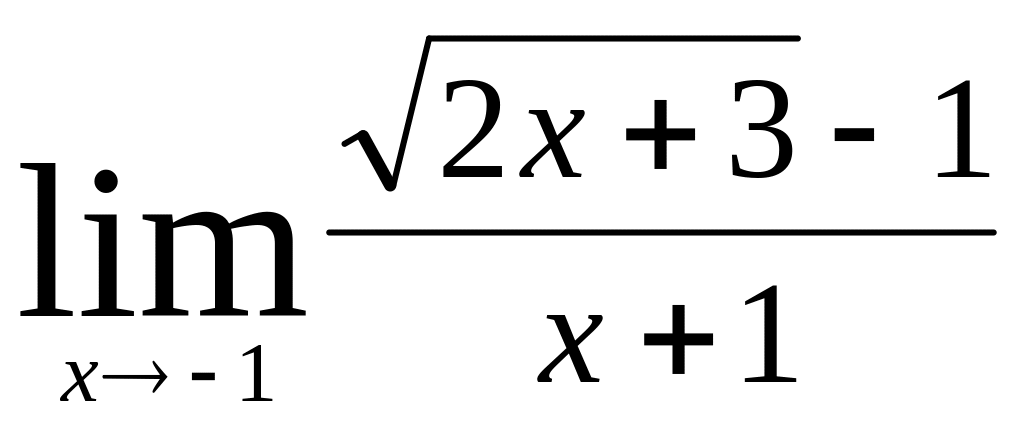 ;
;г)
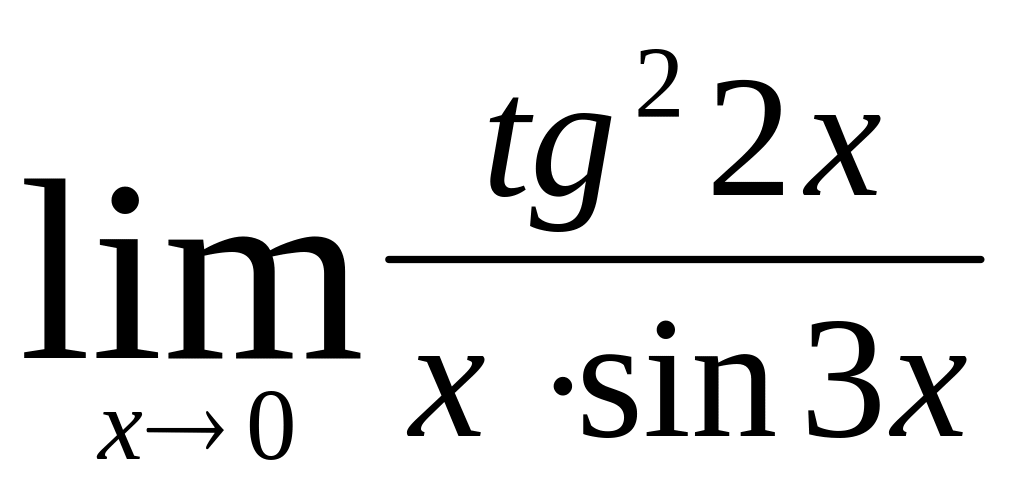 .
.а)
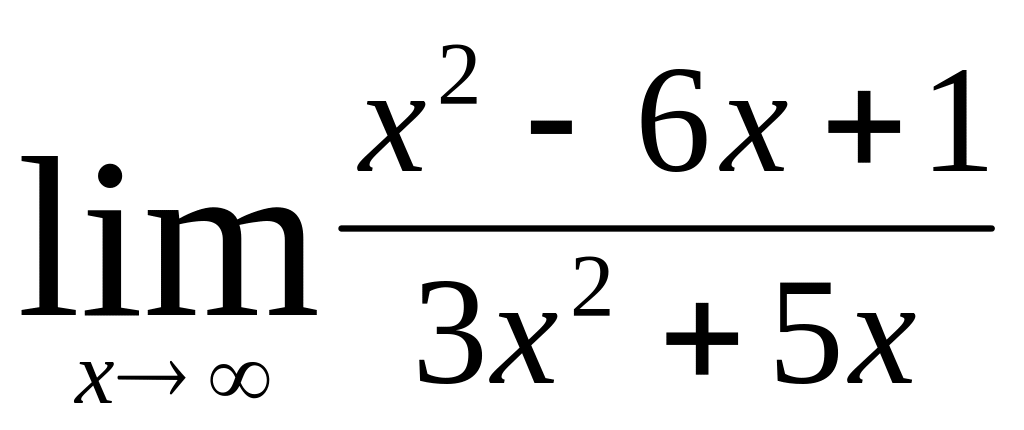 ;
;б)
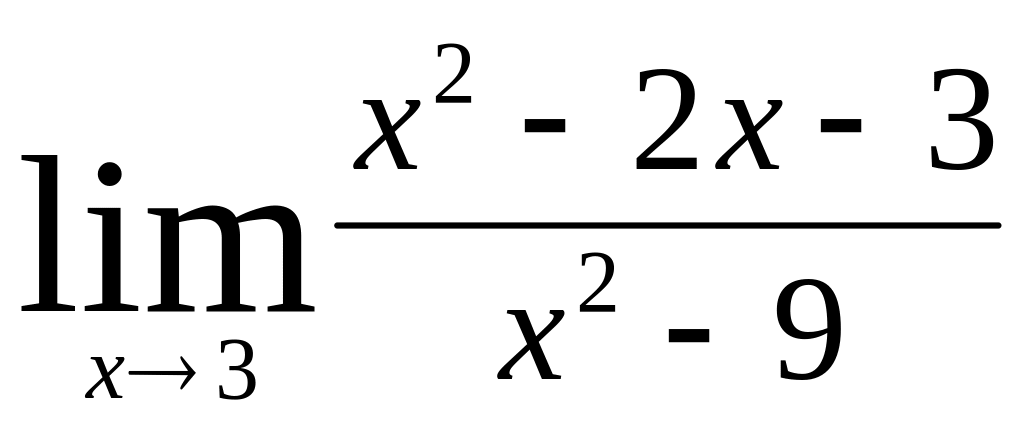 ;
;в)
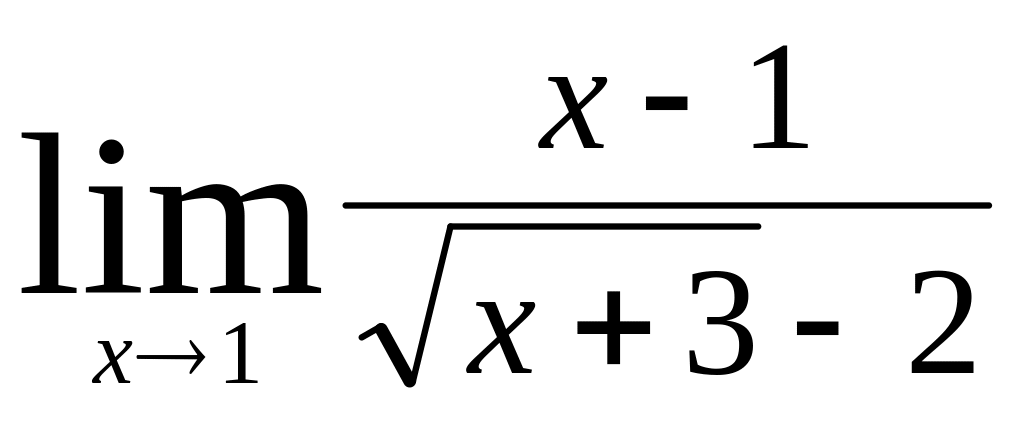 ;
;г)
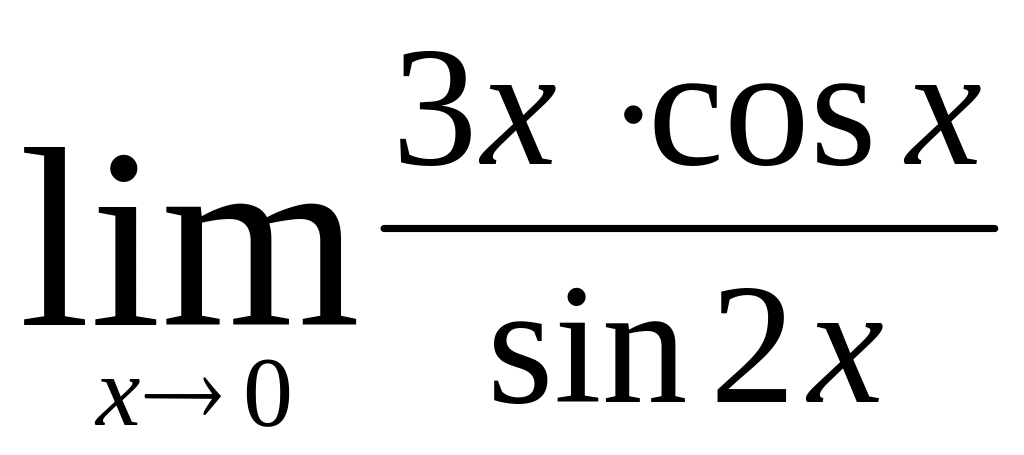 .
.а)
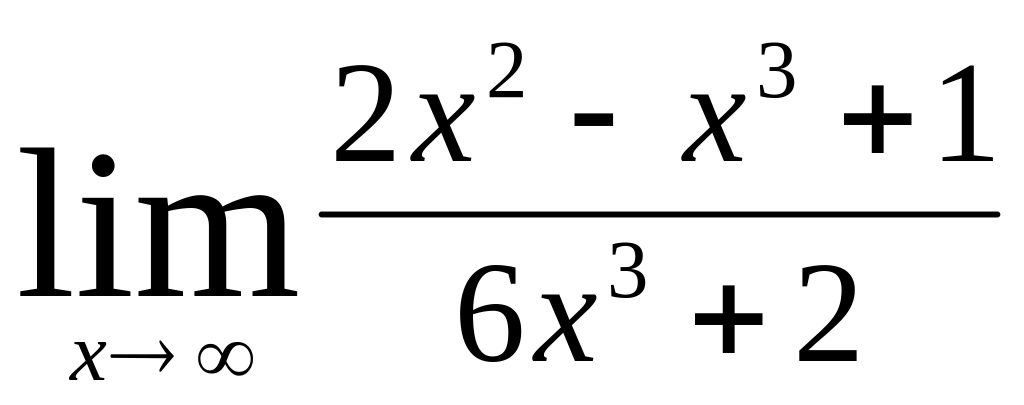 ;
;б)
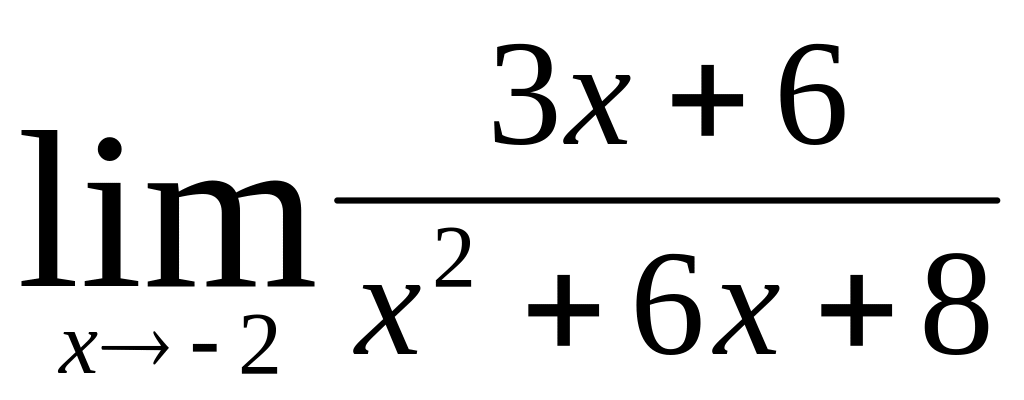 ;
;в)
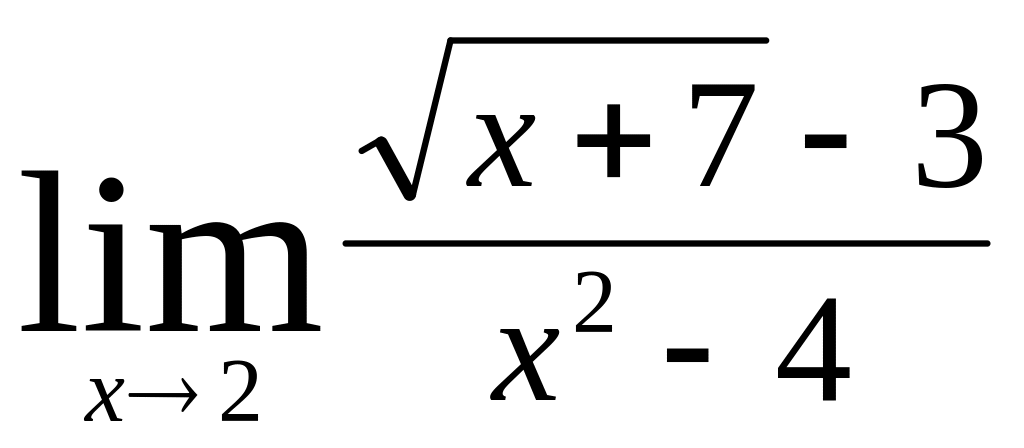 ;
;г)
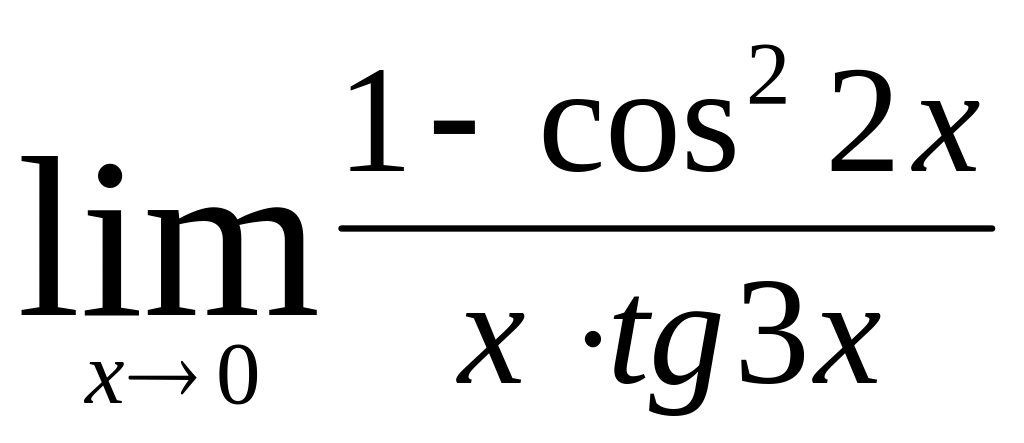 .
.
Задание 2.2.
Исследовать на непрерывность данные функции, указать точки разрыва и их характер. Выполнить схематический чертеж.
-
а)
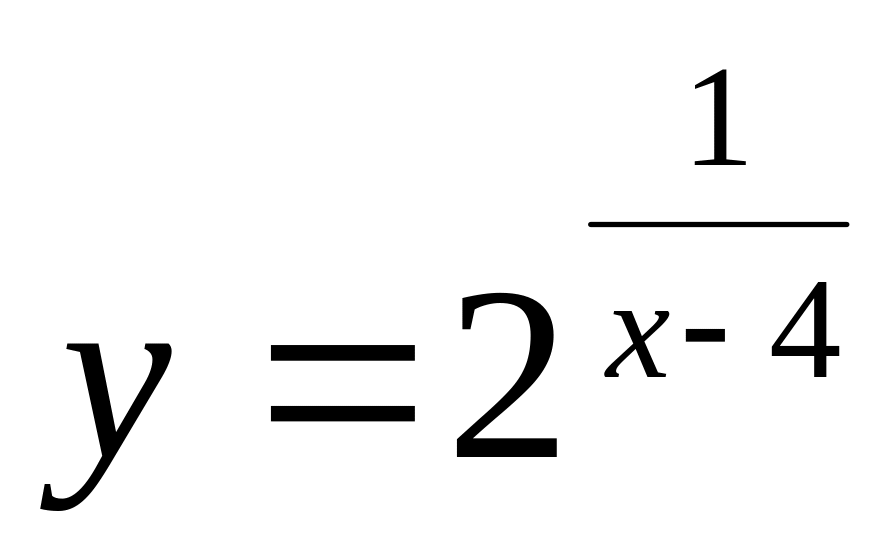 ;
;
б)
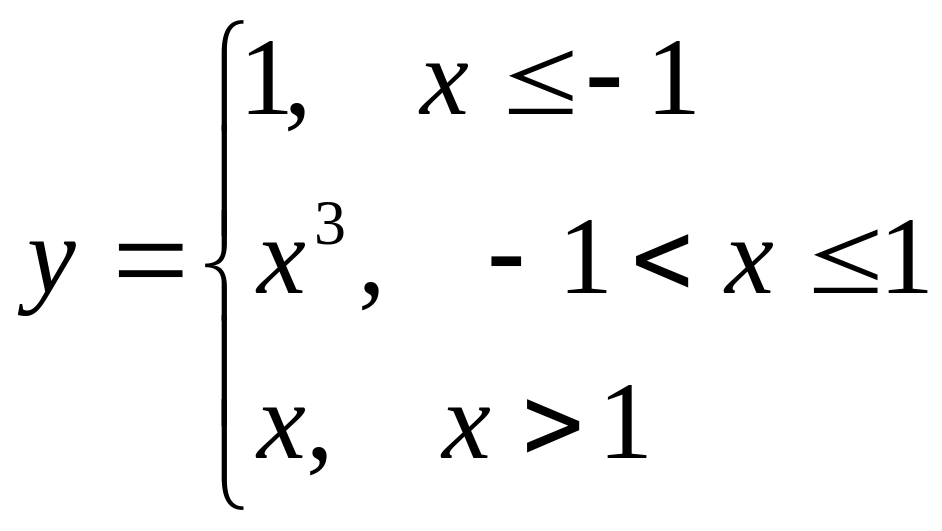 .
.а)
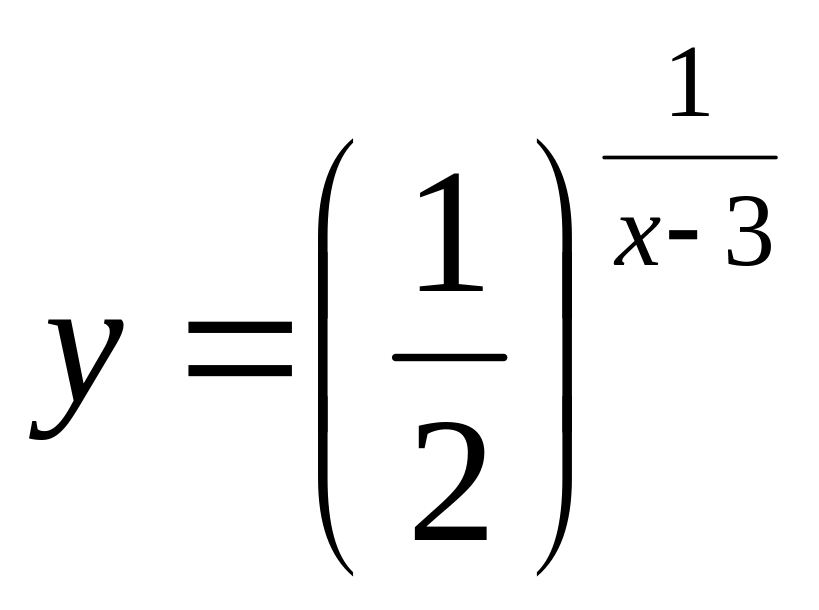 ;
;
б)
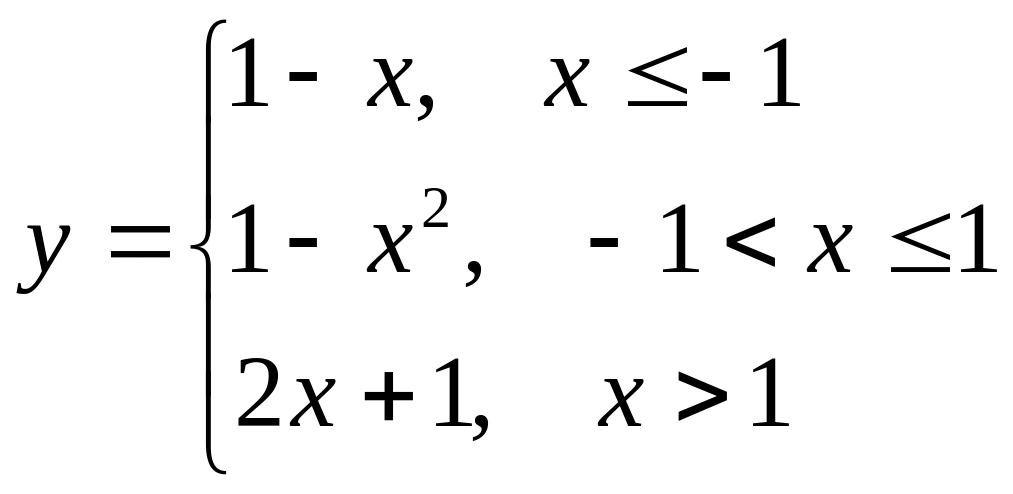 .
.а)
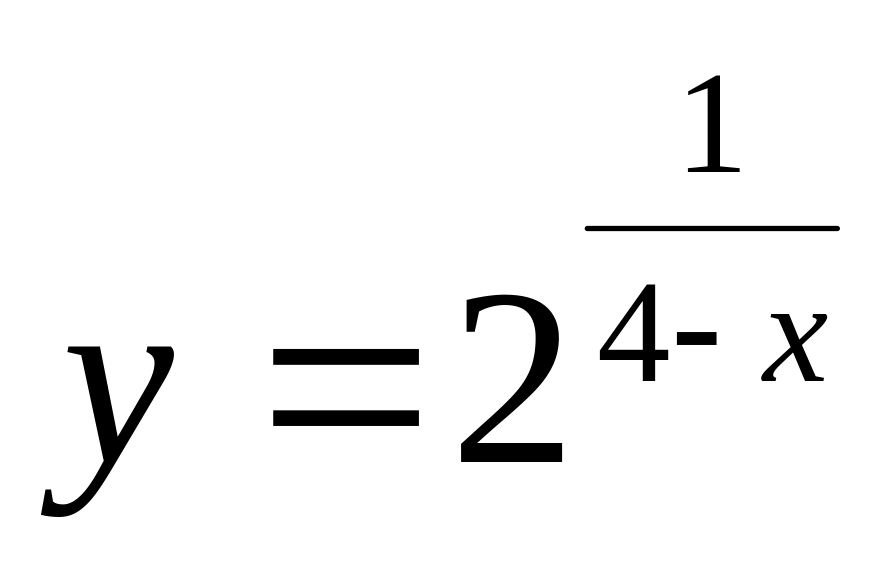 ;
;
б)
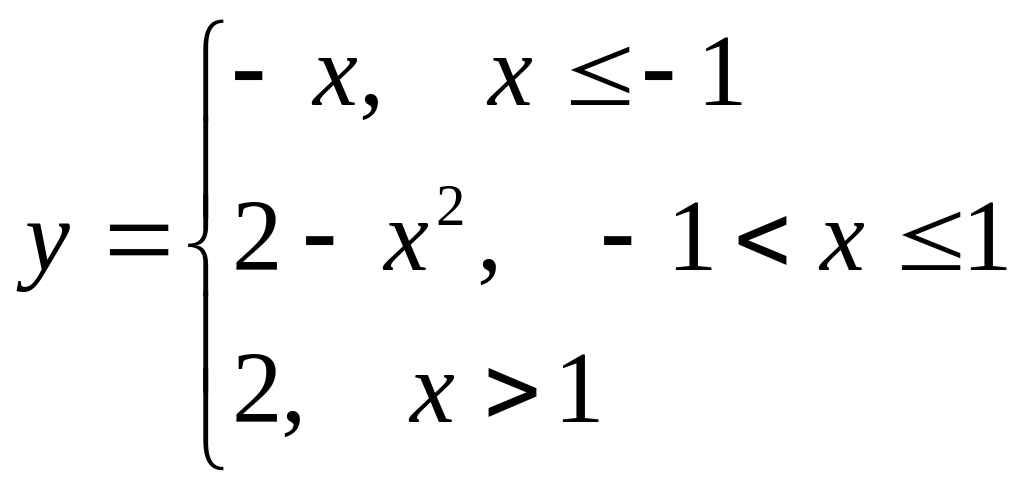 .
.а)
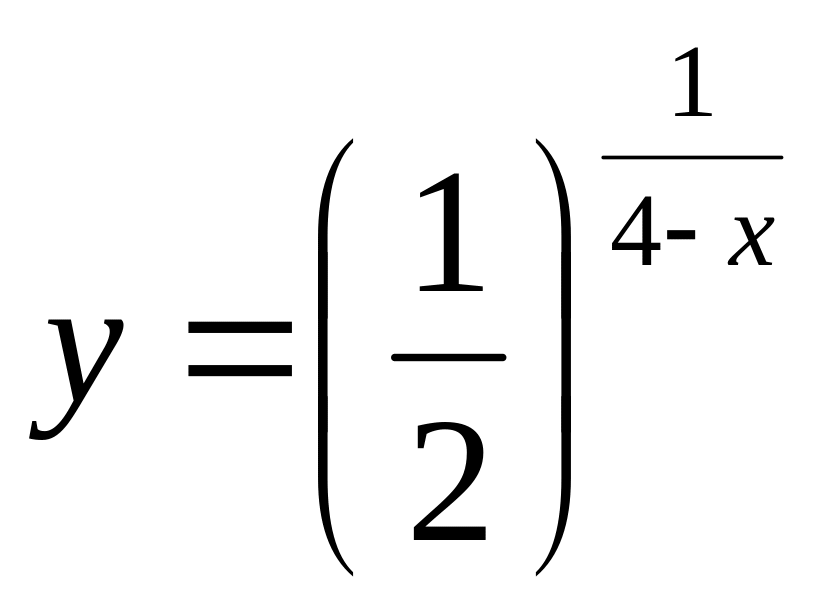 ;
;
б)
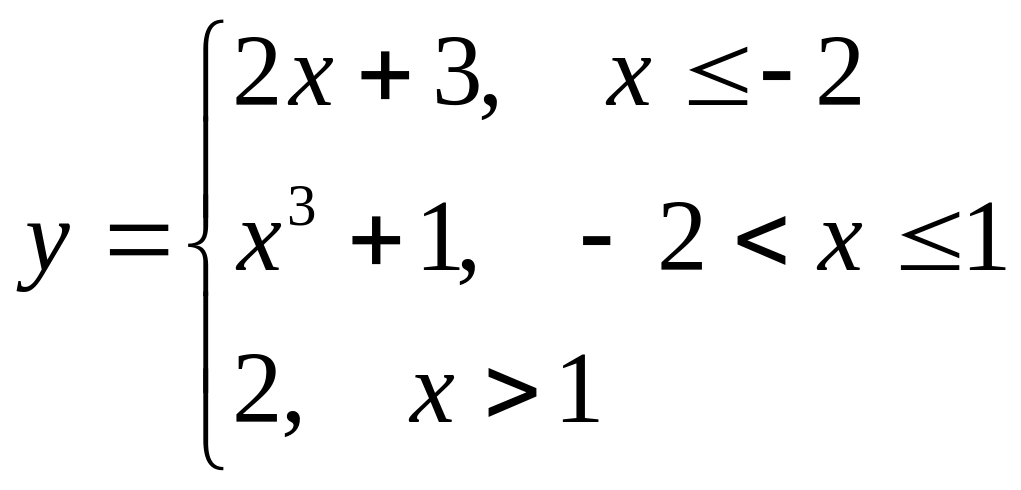 .
.а)
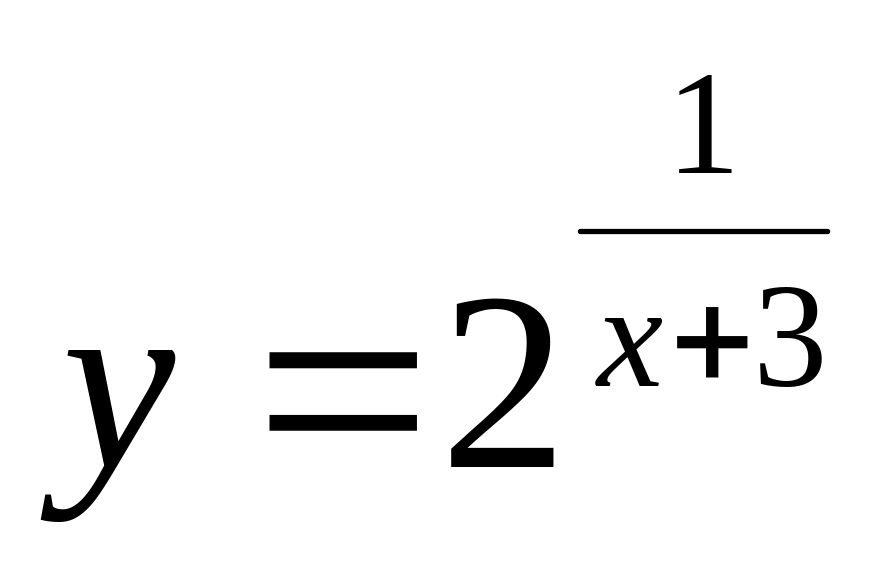 ;
;
б)
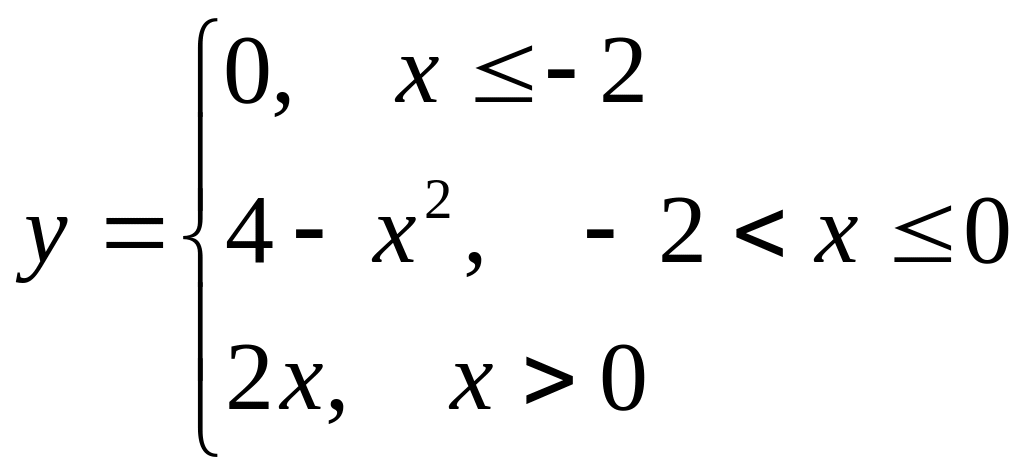 .
.а)
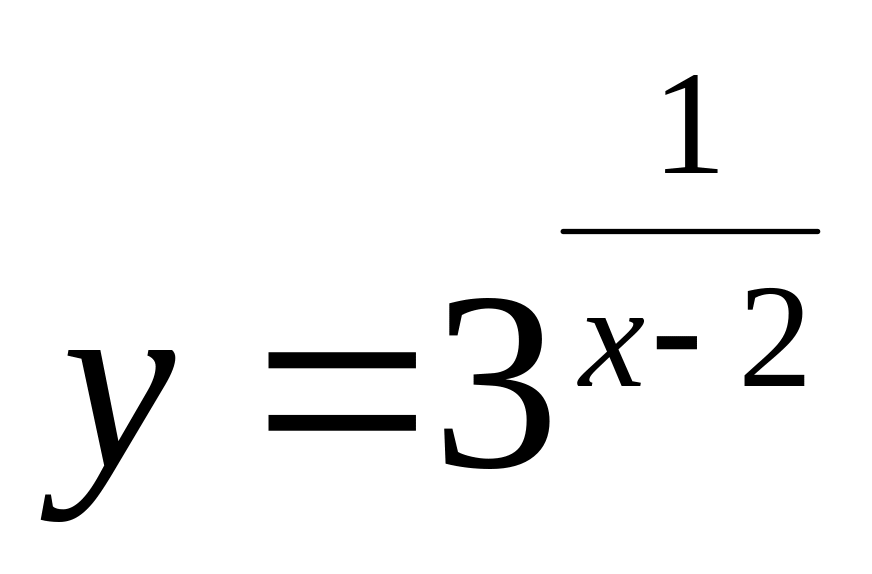 ;
;
б)
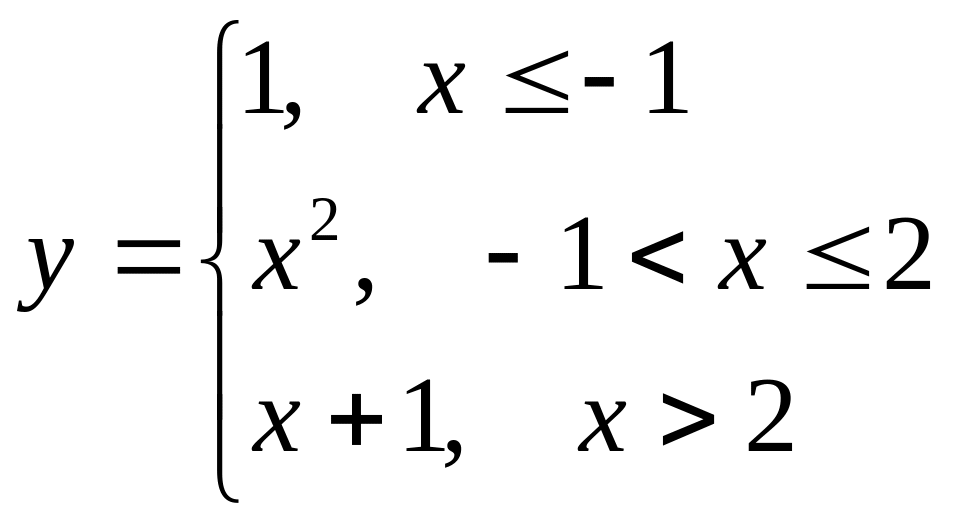 .
.а)
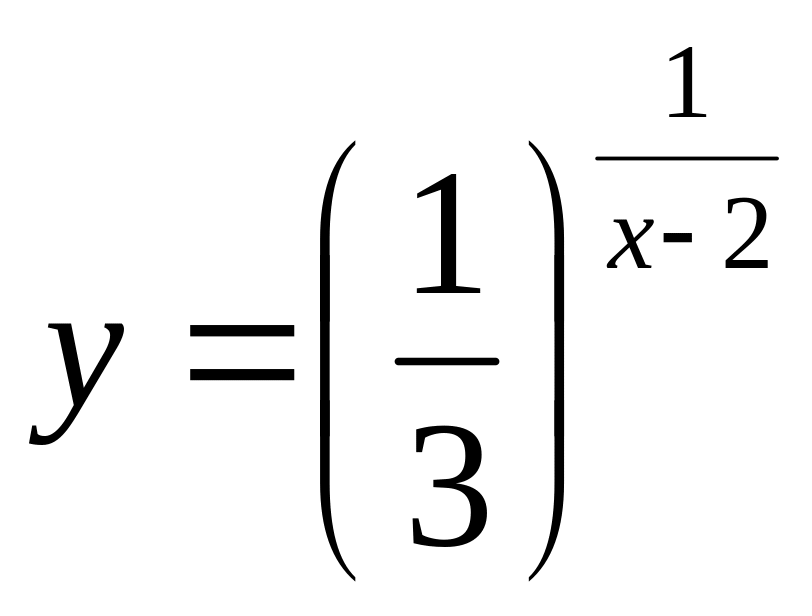 ;
;
б)
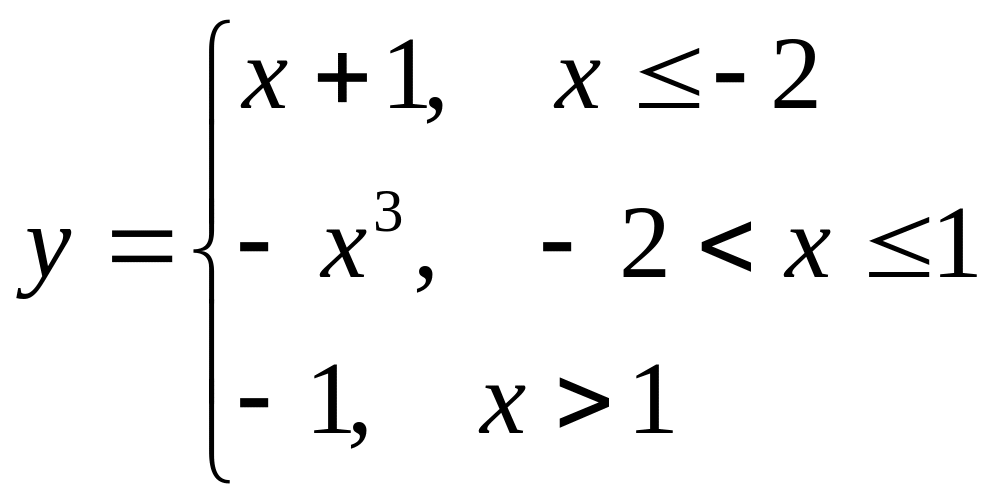 .
.а)
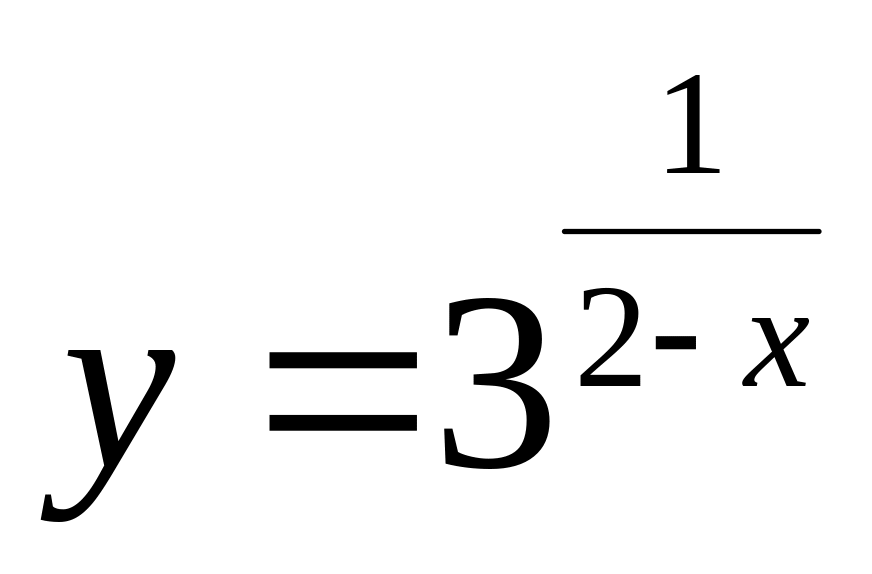 ;
;
б)
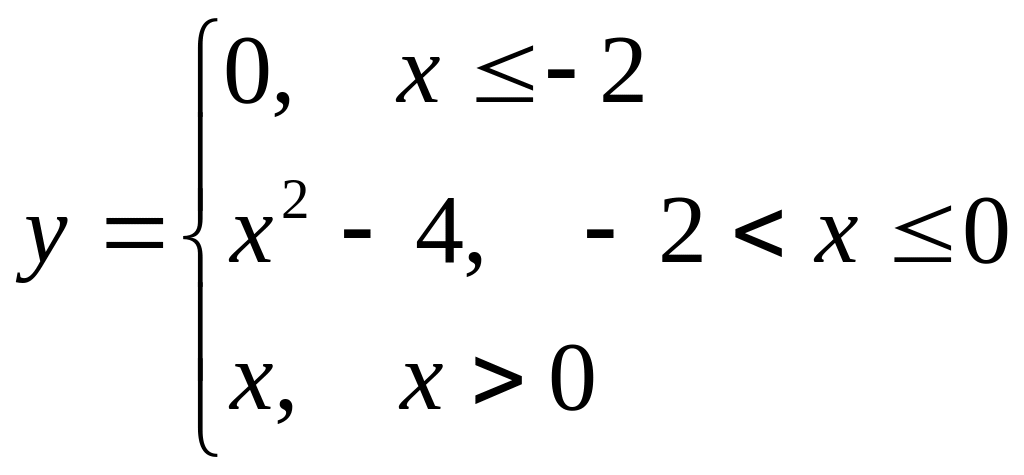 .
.а)
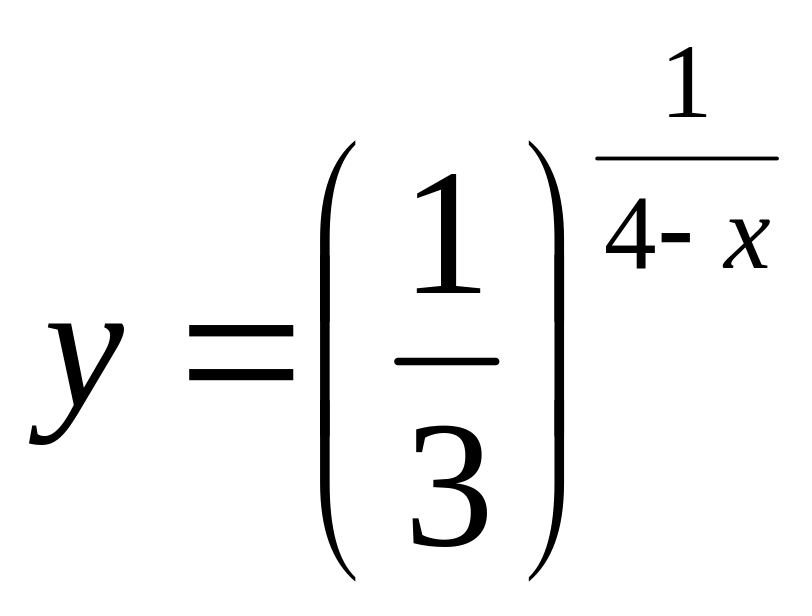 ;
;
б)
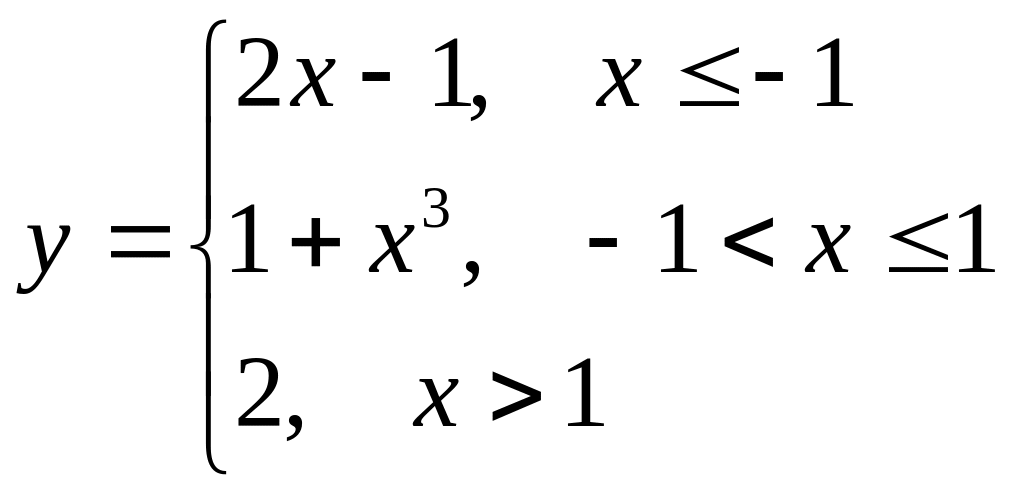
а)
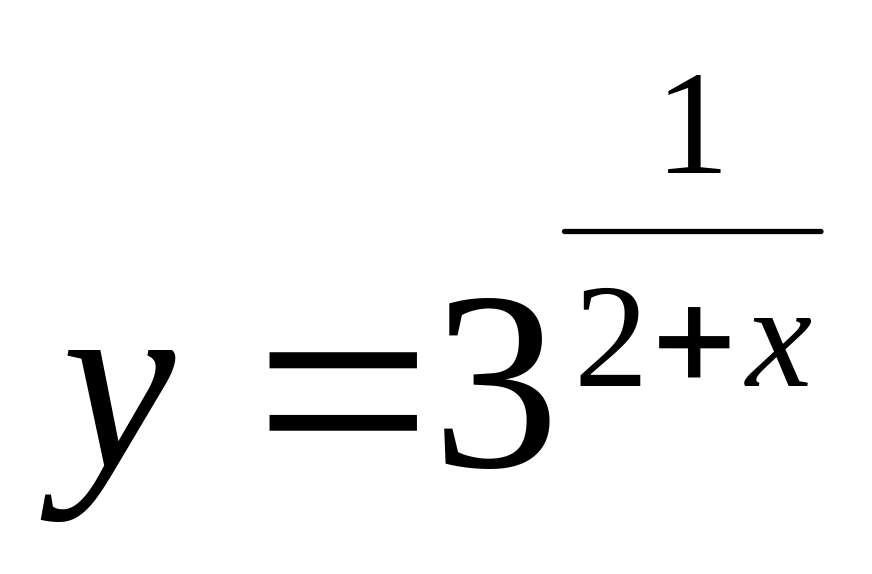 ;
;
б)
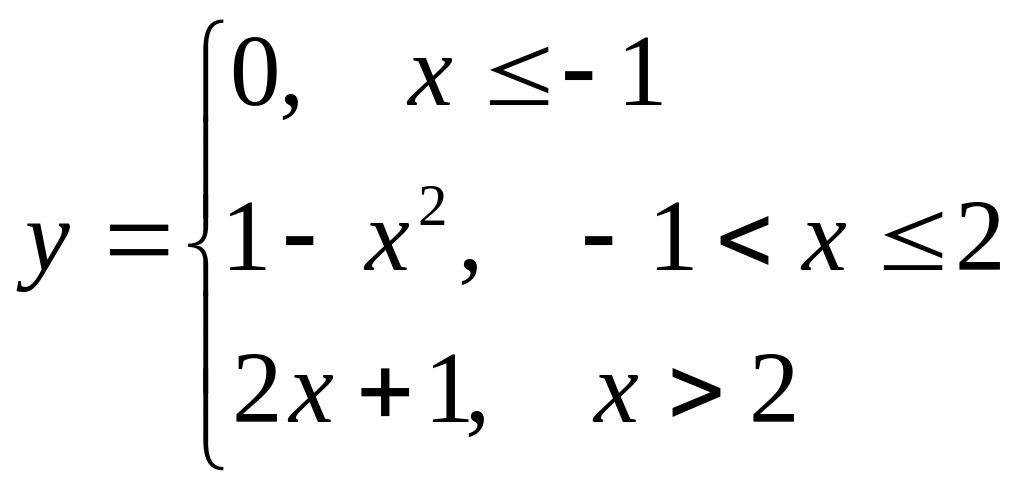
Задание 2.3.
Вычислить производные данных функций.
-
а)
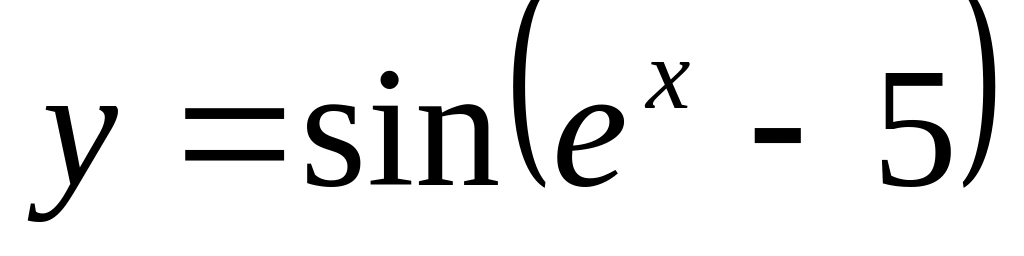 ;
;б)
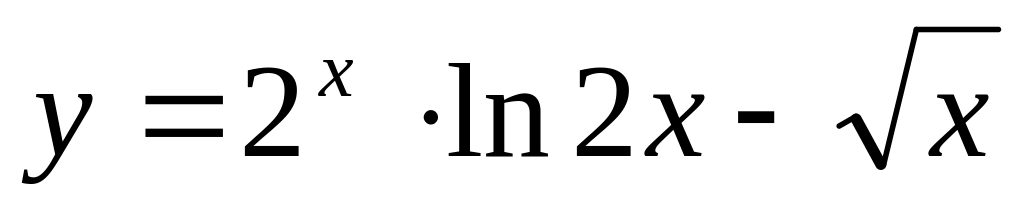 ;
;в)
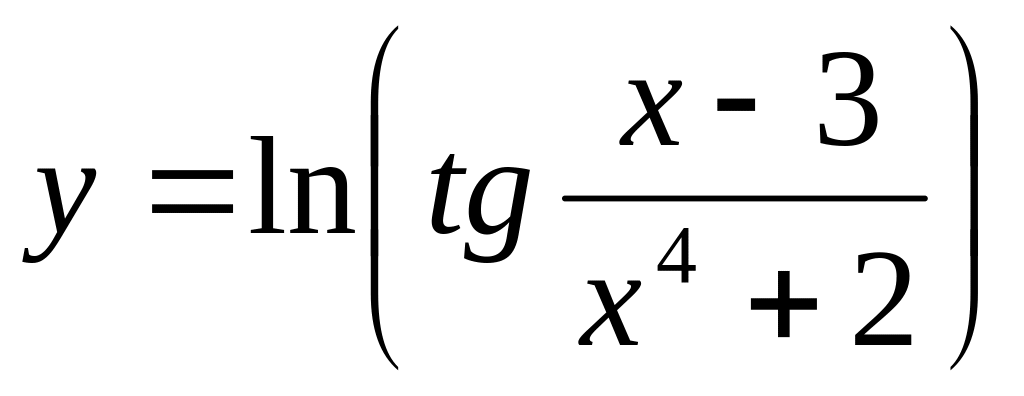 .
.а)
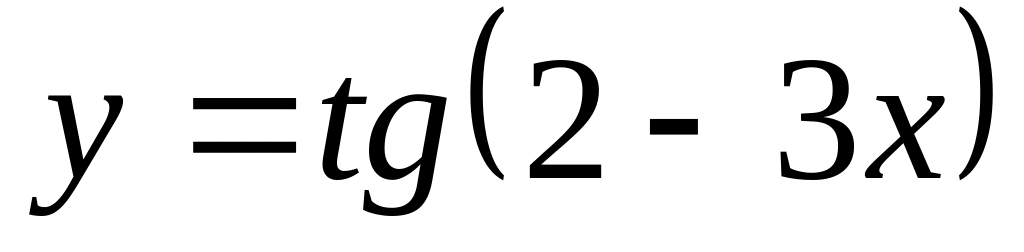 ;
;б)
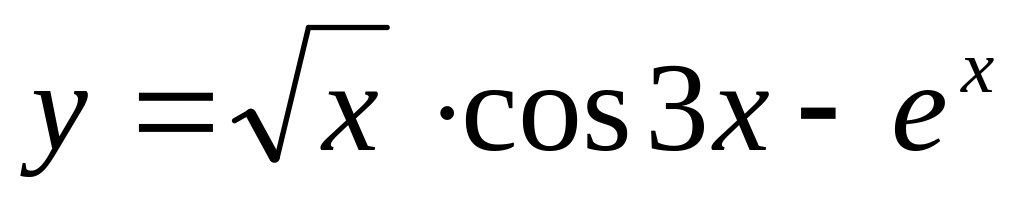 ;
;в)
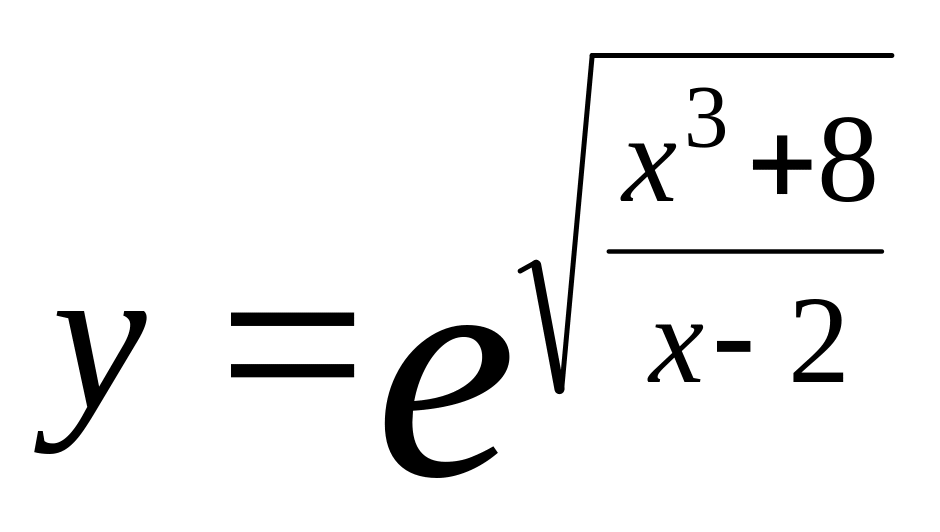 .
.а)
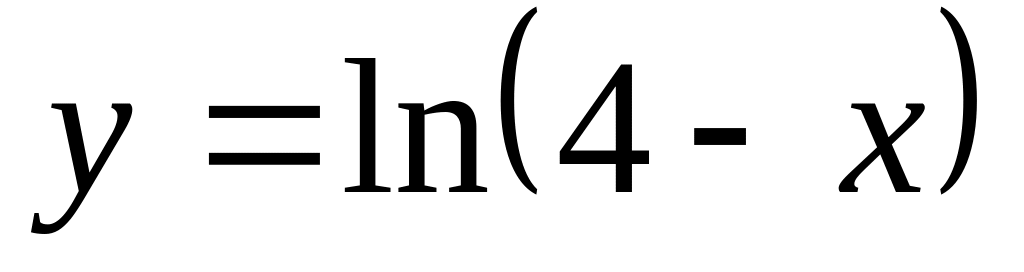 ;
;б)
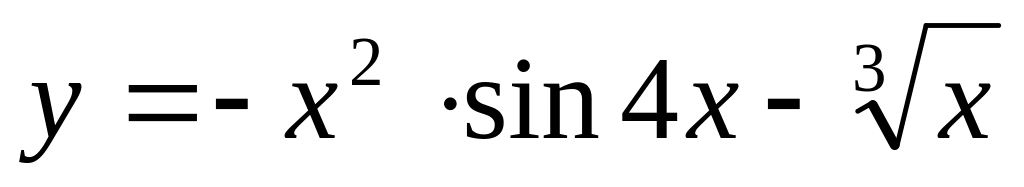 ;
;в)
 .
.а)
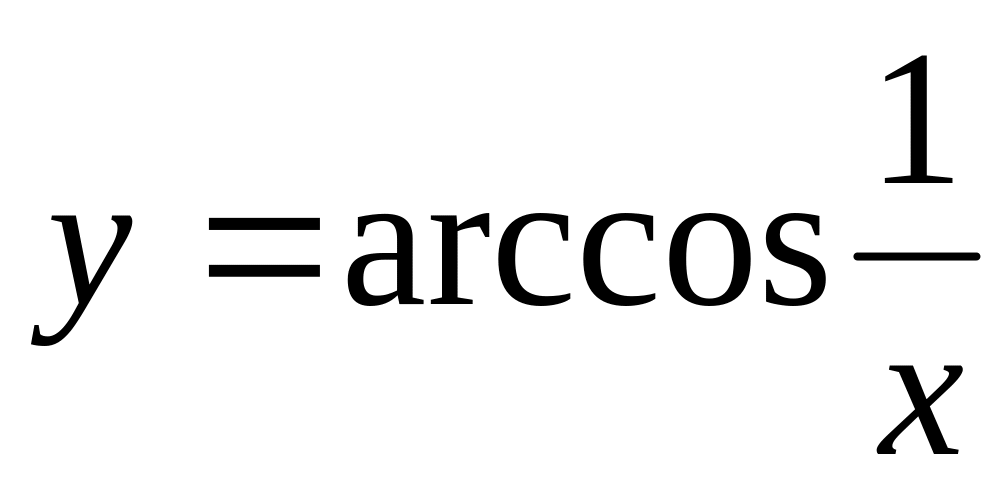 ;
;б)
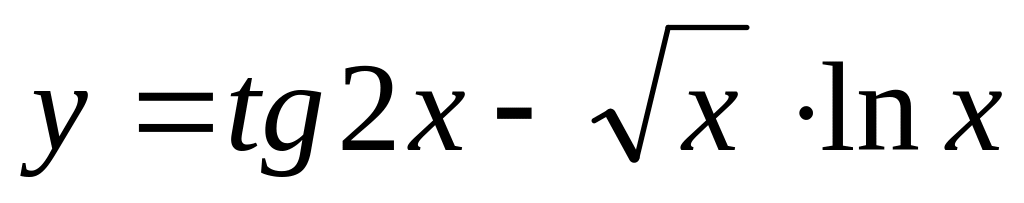 ;
;в) .
а)
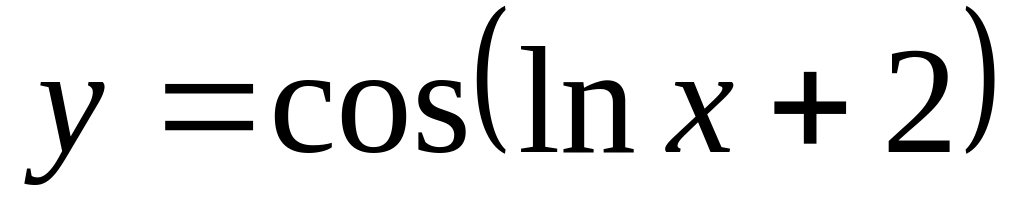 ;
;б)
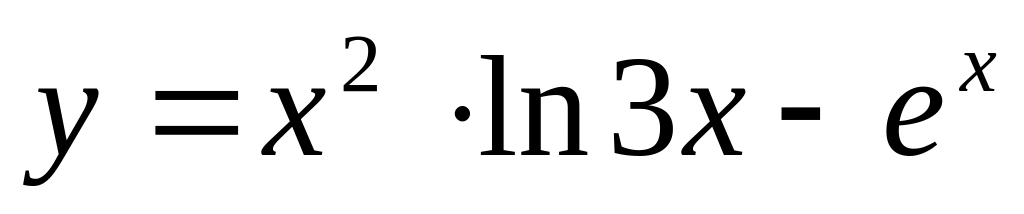 ;
;в)
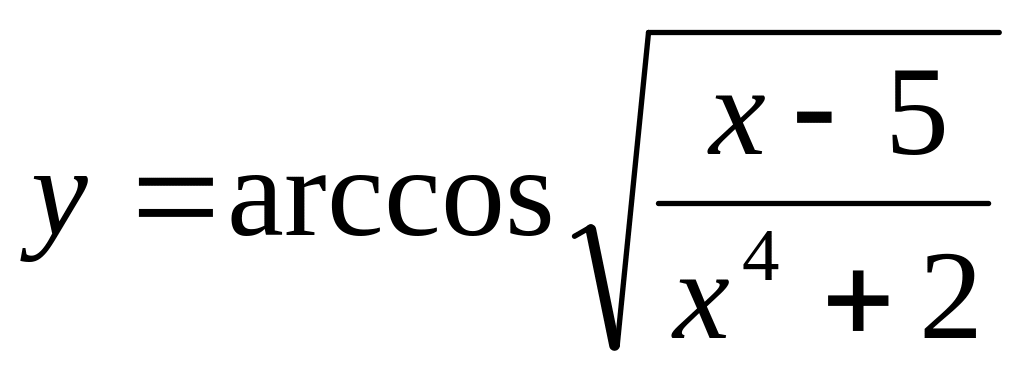 .
.а)
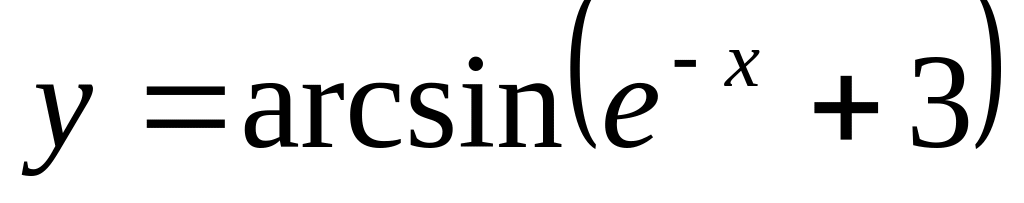 ;
;б)
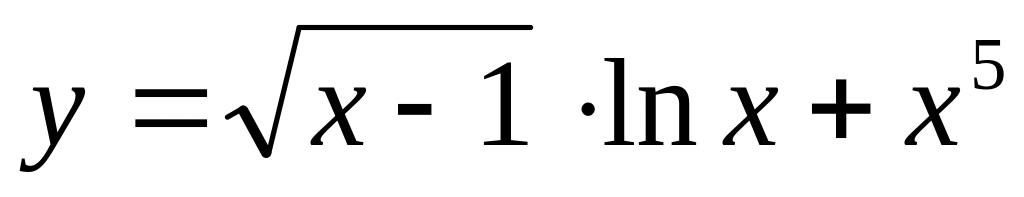 ;
;в)
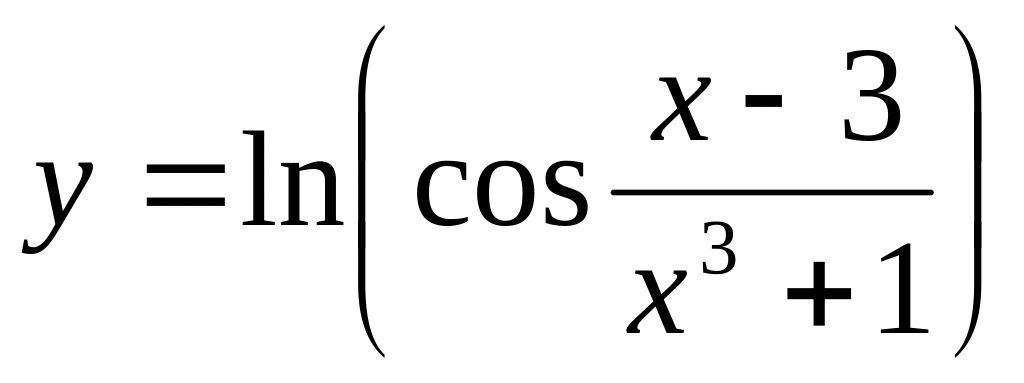 .
.а)
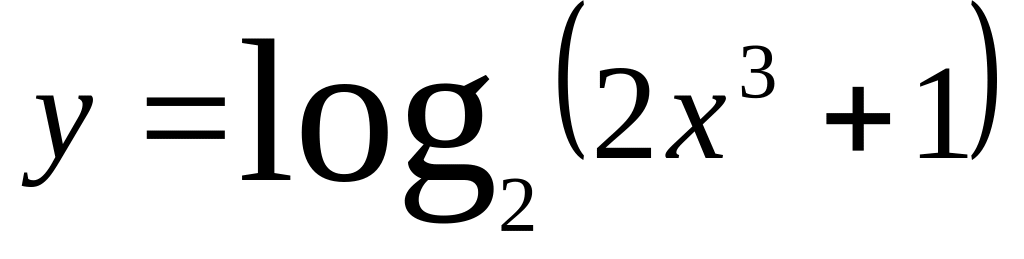 ;
;б)
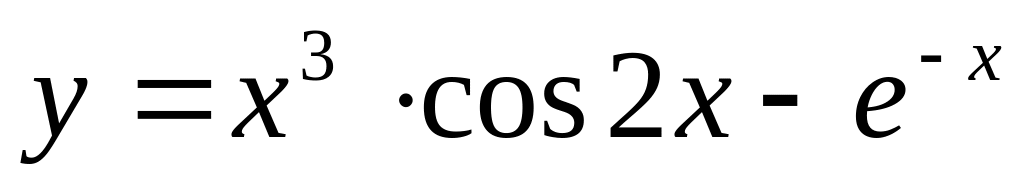 ;
;в)
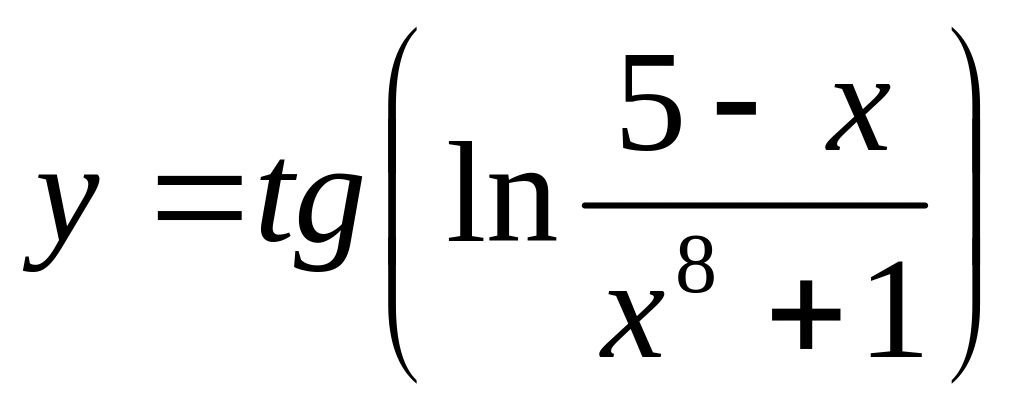 .
.а)
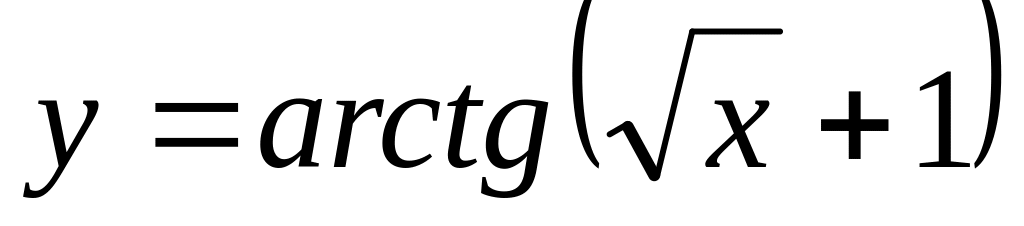 ;
;б)
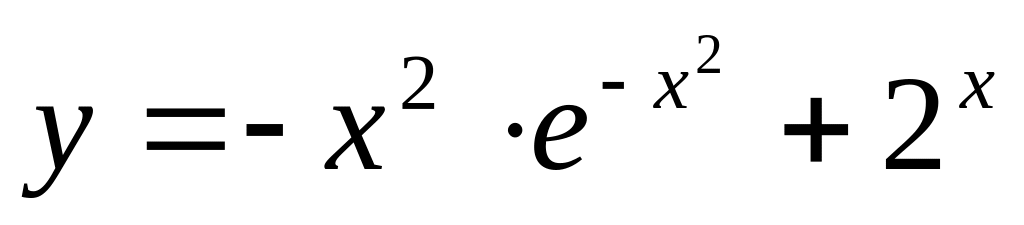 ;
;в) .
а)
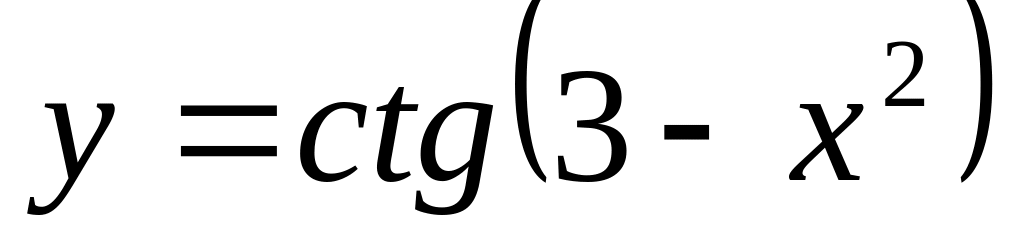 ;
;б)
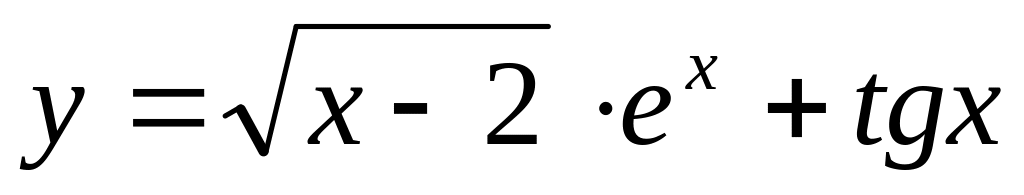 ;
;в)
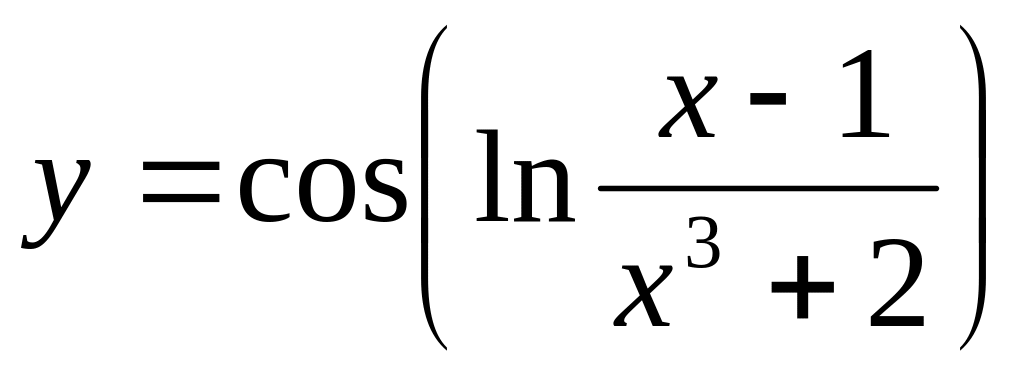 .
.а)
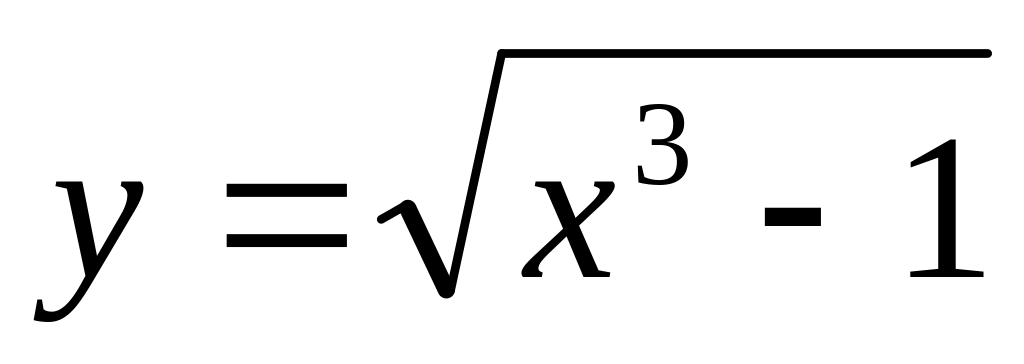 ;
;б)
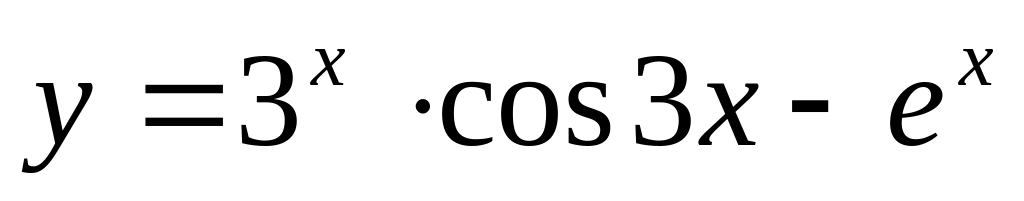 ;
;в)
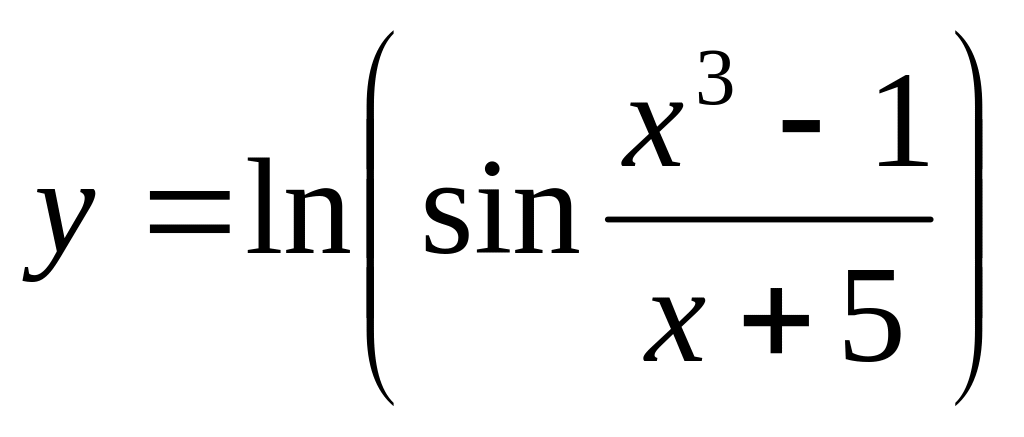 .
.
Задание 2.4.
Дана функция
z=f(x;y).
Найти частные производные второго
порядка
![]() ,
,
![]() .
Убедиться, что смешанные производные
.
Убедиться, что смешанные производные
![]() и
и
![]() равны.
равны.
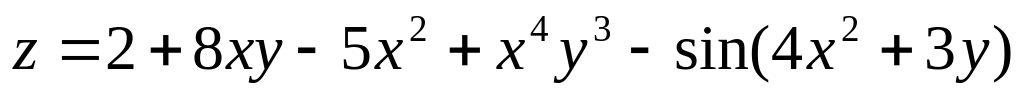 .
. .
. .
.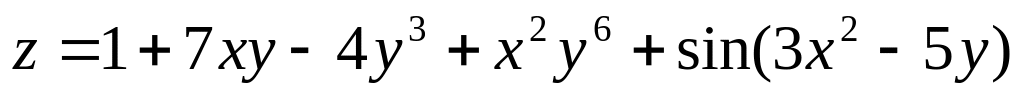 .
.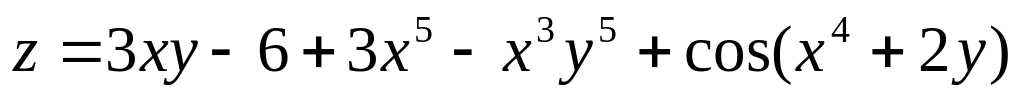 .
.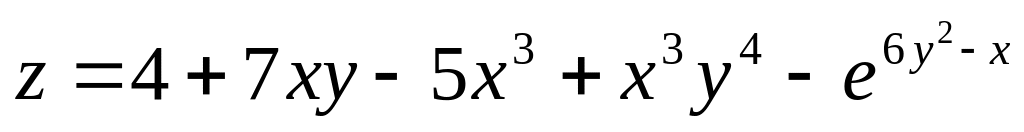 .
.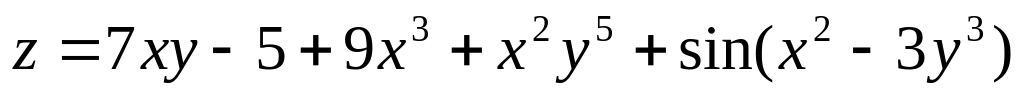 .
.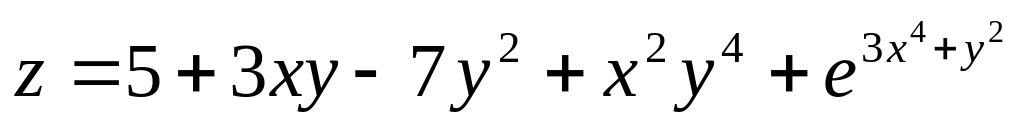 .
.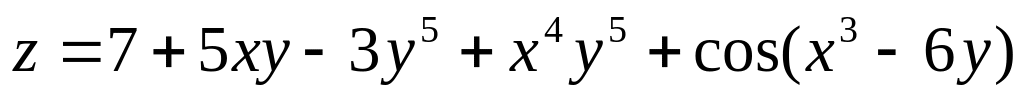 .
.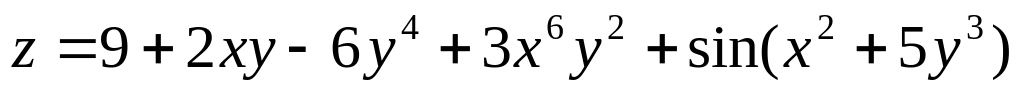 .
.
