2.3. Фазовый переход ферромагнетик-парамагнетик для коллективизированных моментов. Парамагнетизм Паули. Критерий Стонера. Зонный метамагнетизм. Спиновые флуктуации. Пиромагнетизм.

В металлах, сплавах, интерметаллических соединениях наряду с локализованными электронами имеются электроны, которые отрываются от ионов и коллективизируются. Эти электроны легко двигаются в кристаллической решетке, обусловливая высокую проводимость. Можно представить металл как решетку из ионов, омываемую газом коллективизированных электронов. Электростатические силы отталкивания между электронами в первом приближении компенсируются силами притяжения между электронами и ионами. Поэтому в простейшей модели свободных электронов (модели Друде-Лоренца) не учитывается взаимодействие электронов друг с другом.

Каждый электрон обладает спином s_e = 1/2. С учетом g-фактора электрона g_e = 2 каждый электрон несет магнитный момент _e = g_es_e = 1 _B. Поэтому можно было бы ожидать, что в случае свободных электронов классический газ магнитных стрелок (магнитных диполей) должен обладать такой же парамагнитной восприимчивостью как и система невзаимодействующих локализованных моментов, то есть должен выполняться закон Кюри (2.12). Однако магнитная восприимчивость многих металлов и сплавов почти не зависит от температуры и ее величина значительно меньше рассчитанной из закона Кюри. Эти особенности магнитных свойств металлов были объяснены в 1928 году швейцарским ученым В. Паули, который показал, что электронный газ нельзя рассматривать в классическом приближении, а необходимо учитывать, что электроны являются квантовыми объектами и подчиняются квантовой статистике Ферми, отличающейся от классической статистики Больцмана.

Квантовый характер электрона приводит к тому, что для электронного газа должен выполняться принцип Паули: в каждом энергетическом квантовом состоянии может находиться не более двух частиц с полуцелыми спинами. Поэтому, в отличие от статистики Больцмана, все частицы не могут находиться в наинизшем энергетическом состоянии. Между соседними уровнями энергетическое расстояние должно удовлетворять принципу неопределенности, согласно которому состояние квантовых частиц, близких по энергии, можно различить, если произведение изменения координат на изменение импульсов равно постоянной Планка h:

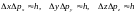. (1)

Пусть в куске металла, представляющем собой куб с ребром L и объемом V находятся N невзаимодействующих электронов. Мы не интересуемся положением электрона в пределах этого куба. Тогда элементарный квантовый объем в пространстве импульсов составит

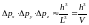. (2)

При Т = 0 все n электронов заполняют в p – пространстве сферу, радиус которой P_F определяется из условия, что каждый элементарный объем h³/V в сфере объемом 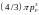содержит по 2 электрона:

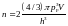. (3)

Максимально возможные значения импульса

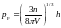(4)

получили название импульса Ферми, а соответствующее ему значение энергии

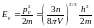. (5)

называется энергией Ферми.

Число электронных состояний dn, имеющих энергию от E до E + dE равно удвоенному числу элементарных квантовых ячеек в p – пространстве в сферическом слое радиусом 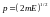и толщиной 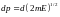. Следовательно, плотность электронных состояний для кристалла единичного объема равна

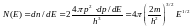. (6)

Зависимость плотности состояний свободных электронов от энергии приведена на рис. 2. Сплошная вертикальная линия – положение уровня Ферми. При повышении температуры уровень Ферми размывается (штриховая линия), так как из-за термических возбуждений заполняются электронные состояния, лежащие выше уровня Ферми.

Величину энергии Ферми можно оценить с использованием (5). Плотность электронов в металле составляет 10²² – 10²³ см^-3. Учитывая, что масса электрона m = 9.1 10^-28 г и постоянная Планка h = 6.62 10^-27 эрг, находим E_F = 10^-11 – 10^-12 эрг. Эта энергия соответствует температуре Ферми T_F = E_F/k_B = 10⁴ – 10⁵ К (k_B = 1.38 10^-16 эрг/К). Таким образом, квантовый характер поведения электронного газа сохраняется до высоких температур. При учете взаимодействия электронов с кристаллической решеткой картина принципиально не изменяется, но кривая плотности состояний становится более сложной.

В магнитном поле энергии электронов с противоположно ориентированными спинами различаются (рис. 2). Энергетическая зона разбивается на две подзоны, сдвинутые друг относительно друга на величину 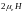, где _e = 1 _B. Часть электронов из энергетически невыгодной подзоны (-) перейдет в выгодную подзону (+). При этом возникает магнитный момент

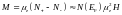. (7)

Таким образом, магнитная восприимчивость электронного газа

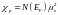. (9)

не зависит от температуры. Этот вывод отражает слабое влияние термических возбуждений на электроны вблизи уровня Ферми, которые обладают температурой Ферми порядка 10⁴ – 10⁵ К.

В системе невзаимодействующих электронов фазовые переходы отсутствуют. Если между электронами существует положительное обменное взаимодействие, то оно стремится выстроить все спины параллельно. В результате обменное взаимодействие ведет к усилению парамагнитной восприимчивости:

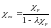, (10)

где  = I/_B². Из формулы (10) видно, что восприимчивость обменно-усиленного парамагнетика возрастает по мере возрастания _p. При выполнении условия _p = 1 восприимчивость стремится к бесконечности. Значит, обменное взаимодействие приводит к самопроизвольному ферромагнитному упорядочению. С учетом (9) условие возникновения ферромагнетизма в системе коллективизированных электронов, которое носит название критерия Стонера, имеет вид:

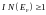. (11)

Различают слабые и сильные ферромагнетики. Слабыми называют ферромагнетики, в которых спонтанное расщепление подзон меньше, чем энергетическая ширина зоны. Они характеризуются небольшим спонтанным моментом и сильной высокополевой восприимчивостью, связанной с тем, что с постом поля продолжается перераспределение электронов между подзонами. В сильных ферромагнетиках все электроны находятся в одной подзоне, и магнитная восприимчивость близка к нулю.

В модели Стонера разрушение ферромагнетизма с ростом температуры должно происходить при температуре порядка температуры Ферми 10⁴ – 10⁵ К. Однако экспериментальные значения температуры Кюри значительно ниже (самая высокая – у кобальта, 1403 К). Этот экспериментальный факт удается объяснить в модели, предложенной Т. Мория, которая учитывает неоднородности намагниченности, изменяющиеся в пространстве и во времени (спиновые флуктуации), амплитуда которых растет при повышении температуры.

Зонный метамагнетизм

Зонный метамагнетизм в обменном поле

Обратный зонный метамагнетизм

Пиромагнетизм.