2.2. Теория Нееля молекулярного поля многоподрешеточных магнетиков. Фазовый переход антиферромагнетик-парамагнетик и ферримагнетик-парамагнетик. Слабый ферромагнетизм.

Антиферромагнетики, как и ферромагнетики, обладают спонтанным упорядочением магнитных моментов. Но магнитные моменты ориентированы в разных направлениях, так что результирующий макроскопический магнитный момент равен нулю. В простейшем случае магнитная структура антиферромагнетика представляет собой суперпозицию двух ферромагнитных подрешеток с одинаковыми магнитными моментами, ориентированными антипараллельно друг другу.

Первое теоретическое описание антиферромагнетизма было выполнено Ландау в 1933 году. Он показал, что несмотря на отсутствие спонтанного магнитного момента при низкой температуре, с ростом температуры в антиферромагнетиках происходит разрушение спонтанного упорядочения в подрешетках, которое сопровождается появлением максимумов магнитной восприимчивости, теплоемкости и других аномалий, соответствующих фазовым переходам 2-го рода. Немного позднее Неель разработал теорию антиферромагнетизма в приближении молекулярного поля. В его честь точка перехода из антиферромагнитного в парамагнитное состояние носит название температуры Нееля.

Рассмотрим подход Нееля к описанию антиферромагнетиков. Пусть в образце есть две подрешетки A и B эквивалентных магнитных ионов. Поля, действующие на каждую из подрешеток, равны

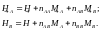(1)

Здесь n_ij – параметры молекулярного поля, М_i – намагниченности подрешеток:

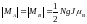(2)

Коэффициенты n_AA = n_BB = n₁ положительны и для антиферромагнетика равны между собой, а коэффициент n_AB = n₂ всегда отрицательный.

Температурная зависимость намагниченности каждой подрешетки определяется функцией Бриллюэна:

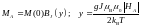(3)

где

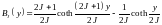(4)

Аналогичное выражение можно записать для подрешетки M_B.

При высоких температурах намагниченность каждой подрешетки равна восприимчивости, определяемой из закона Кюри, умноженной на результирующее (внешнее плюс молекулярное) поле:

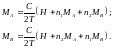(5)

где константа Кюри равна

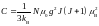6)

Два самосогласованных уравнения для M_A и M_B ведут к возникновению спонтанной намагниченности подрешеток при температуре Неля T_N, когда детерминант коэффициентов равен нулю:

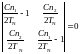(7)

Отсюда 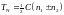. Поскольку коэффициент n₂ всегда отрицательный, а температура Неля не может принимать отрицательные значения, физический смысл имеет лишь решение

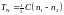(8)

Для температур выше T_N

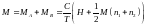(9)

Поскольку  = M/H, получаем

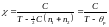(10)

где парамагнитная температура Кюри задается соотношением

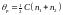(11)

Из уравнения (10) следует, что восприимчивость антиферромагнетика, как и для ферромагнетика, подчиняется закону Кюри-Вейсса. Но антиферромагнитная температура _p не равна температуре магнитного упорядочения. Из сравнения (8) и (11) следует, что всегда _p < T_N. Более того, если константа межподрешеточного обмена больше константы внутриподрешеточного обмена (это выполняется для большинства антиферромагнетиков), парамагнитная температура Нееля будет отрицательной. Восприимчивость при температуре Нееля равна

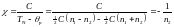(12)

В магнитоупорядоченной области для монокристалла восприимчивости вдоль оси антиферромагнетизма (в направлении выстраивания магнитных подрешеток) и в перпендикулярном направлении будут различаться. Выражение для параллельной восприимчивости может быть получено из (5) с учетом (3). 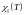оказывается монотонной функцией. При Т = 0 имеем 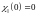, а в точке Нееля . Когда внешнее поле приложено перпендикулярно намагниченностям подрешеток оно отклоняет моменты на угол  и индуцирует перпендикулярный момент

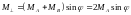(13)

Равновесное положение векторов намагничивания скошенной структуры определяется из условия, что вращающий момент на подрешетку, вызванный внешним полем, компенсируется обратным вращающим моментом молекулярного поля другой подрешетки:

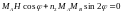(13)

Отсюда получаем, что

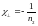(14)

то есть перпендикулярная восприимчивость антиферромагнетика не зависит от температуры.

Примеры антиферромагнетиков

Сложности определения T_N магнитными методами

Магнитная нейтронография.

Ферримагнетики

В отличие от антиферромагнетиков, в ферримагнетиках магнитные моменты двух противоположно направленных подрешеток A и B не равны между собой. Поэтому они обладают спонтанным магнитным моментом. При нуле температур его величина равна

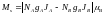(15)

Теория молекулярного поля по отношению к ферримагнетикам позволяет получить примерно те же результаты, какие были получены для антиферромагнетиков. Аналогично (5), для температур выше температуры магнитного упорядочения имеем:

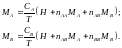(16)

где C_A и C_B – константы Кюри для каждой подрешетки. Из равенства нулю детерминанта

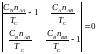(17)

получаем выражение для температуры Кюри:

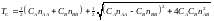(18)

Магнитная восприимчивость ферримагнетика при высоких температурах следует модифицированному закону Кюри-Вейсса:

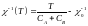(19)

где

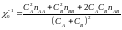(20)

Как правило, при использовании теории молекулярного поля для двухподрешеточных ферримагнетиков пренебрегают наиболее слабыми взаимодействиями. Так например, для 4f-3d интерметаллидов с железом взаимодействие R-R намного слабее взаимодействия Fe-Fe. В этом случае можно считать, что парамагнитная по своей природе подрешетка R упорядочена в молекулярном поле, действующем со стороны подрешетки Fe. Температурная зависимость магнитного момента подрешетки R определяется только обменным взаимодействием со стороны подрешетки Fe:

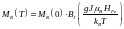(21)

где H_Fe - молекулярное поле, действующее на полный момент J иона R со стороны подрешетки Fe. Величина H_Fe зависит от температуры так же, как зависит от температуры момент подрешетки Fe, поскольку именно этим моментом и создается молекулярное поле:

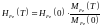(22)

Таким образом, для экспериментального определения молекулярного поля межподрешеточного обмена нужно знать лишь температурную зависимость спонтанного момента и момента подрешетки Fe (ее обычно берут из данных для аналогичного соединения с немагнитными R ионами). От температурного хода намагниченности подрешетки Fe результат слабо зависит, поскольку момент Fe изменяется заметно только вблизи Тс.

Вследствие различного температурного изменения намагниченности подрешеток, с ростом температуры результирующая намагниченность может как возрастать, так и убывать, а также проходить через точку компенсации.

Слабый ферромагнетизм