- •Операційне числення
- •1.Оригінал та зображення
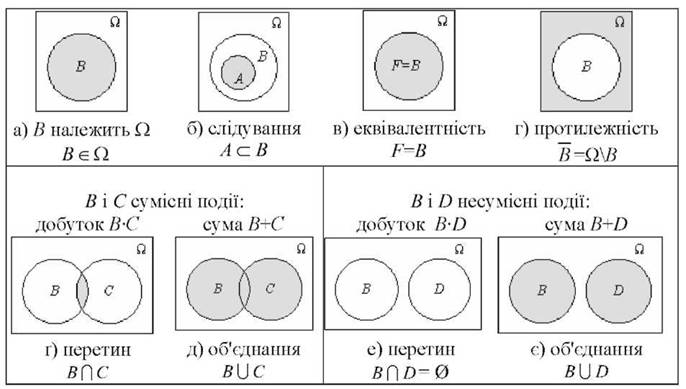
- •2. Подія. Алгебра подій
- •3. Означення ймовірності. (Статистичне, класичне, геометричне).
- •4. Теорема додавання несумісних подій
- •9.Теорема Бернуллі. Теорема Лапласа (інтегральна та локальна)
- •10.Найбілшь ймовірне число появи події. Розподіл Пуассона
- •11.Функція розподілу випадкової величини та ії властивості, графік
- •12.Ймовірність попадання випадкової величини в інтервал (а;в):
- •13.Щільність розподілу неперервної випадкової величини та ії властивості.
- •Властивості
- •Математична статистика
ФКЗ
Означення ФКЗ .Основні геометричні поняття.


Комплексні числа. Дії над ними.


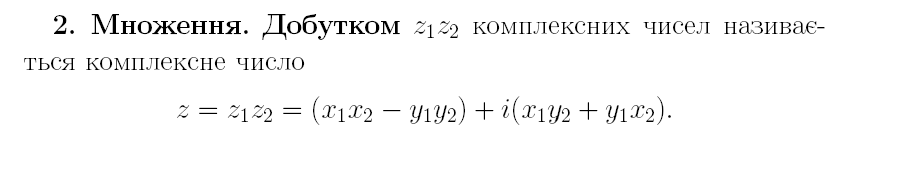
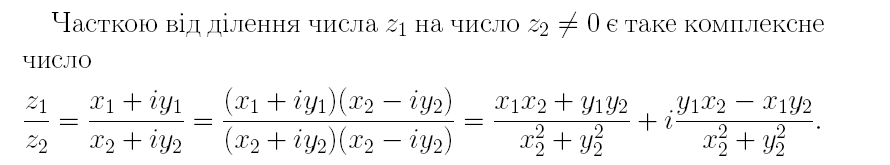
Основні елементарні ФКЗ





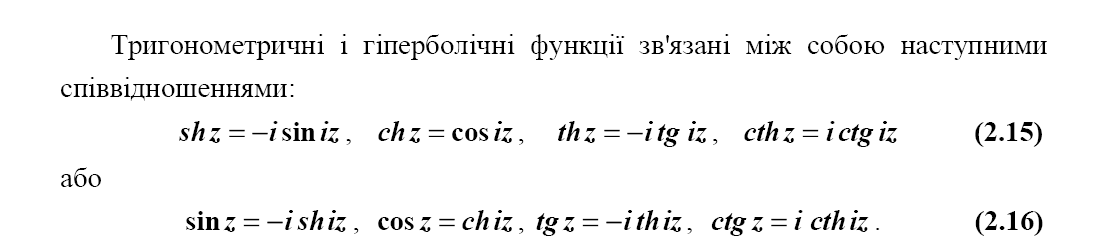

Означення похідної ФКЗ. Аалітичність ФКЗ. Умови Коші-Римана.
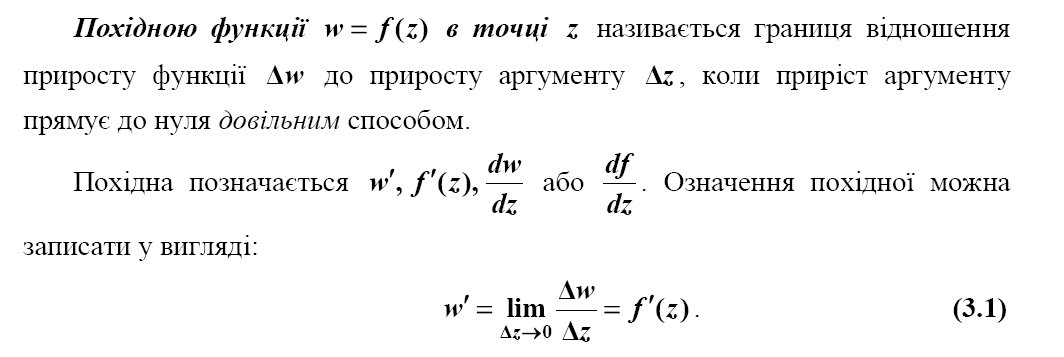


Поняття про конформне відображення. Геометричний зміст модуля та аргумента похідної.


Інтегральна теорема Коші. Формула Коші.

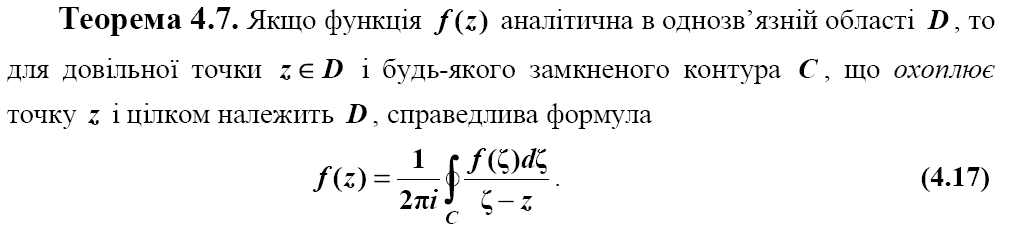
Ряд Лорана.



Класифікація особливих точок.

Поняття лишку. Теорема Коші про лишки.


Операційне числення
1.Оригінал та зображення

2.Теорема про зображення
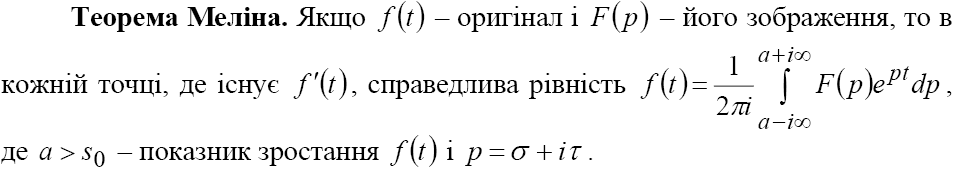
3.Властивості перетворення Лапласа

4.Таблиця зображень


5.Загальна формула обернення
6.Інтеграл Дюамеля.
7. Теорема розкладу.
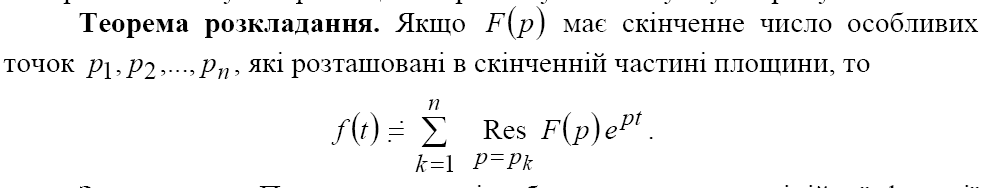
1.Основні формули комбінаторики
Перестановками з
![]() елементів
називаються такі їх сукупності, що
відрізняються одна від іншої тільки
порядком входження елементів. Їх
позначають
елементів
називаються такі їх сукупності, що
відрізняються одна від іншої тільки
порядком входження елементів. Їх
позначають
![]() та
визначають за формулою
та
визначають за формулою
![]()
Розміщеннями з
![]() елементів
по
називаються
такі сукупності
елементів,
що відрізняються одна від іншої принаймні
одним елементом або порядком їх входження
(
елементів
по
називаються
такі сукупності
елементів,
що відрізняються одна від іншої принаймні
одним елементом або порядком їх входження
(![]() ):
):
![]()
Сполученнями з елементів по називаються такі сукупності елементів, що відрізняються одна від іншої принаймні одним елементом ( ) :
![]()
2. Подія. Алгебра подій
Подія – результат випробування.


3. Означення ймовірності. (Статистичне, класичне, геометричне).
Відповідно до класичного визначення ймовірність події А дорівнює відношення кількості випадків, що сприяють настанню події, до загальної кількості випадків.
![]() (1.1)
(1.1)
де Р(А) – ймовірність події А, m – кількість випадків, що сприяють настанню події А, n – загальна кількість випадків.
Статистичною ймовірністю події А називається відносна частота (частість) появи цієї події в n проведених дослідах.
![]()
де P̃(A) – статистична ймовірність події А, w(A) – відносна частість події А, m – кількість дослідів, в яких з’явилася подія А, n – загальна кількість дослідів.
Геометрична ймовірність. Нехай на відрізок L навмання кинута точка. Це означає, що точка обов'язково потрапить на відрізок L і з рівною можливістю може збігтися з будь-якою точкою цього відрізка. При цьому ймовірність потрапляння точки на будь-яку частину відрізка L не залежить від розташування цієї частини на відрізку та пропорційна його довжині. Тоді ймовірність того, що кинута точка потрапить на відрізок l, що є частиною відрізка L, обчислюється за формулою:
![]()
де l - довжина відрізка l, а L - довжина відрізка L.
4. Теорема додавання несумісних подій
Сумою подій А і В називається подія С, яка полягає у здійсненні під час одиничного випробовування або події А, або події В, або обох разом.
![]()
Враховуючи означення суми двох подій і поняття несумісних подій, зауважимо, що сумою С двох несумісних подій А і В є подія, яка полягає в здійсненні або події А, або події В. Одночасна поява подій А і В виключена.
Теорема. Імовірність суми двох несумісних подій дорівнює сумі ймовірностей цих подій, тобто
![]()
5. Теорема додавання довільних подій
Імовірність суми двох довільних випадкових подій А і В дорівнює сумі їх імовірностей без імовірності їхнього добутку, тобто
Р(А + B) = Р(А) + Р(В) - Р(А x B)
6. Теорема добутку незалежних подій
Імовірність добутку двох незалежних подій А і В дорівнює добутку імовірностей цих подій, тобто
![]()
7. Теорема добутку залежних подій
Імовірність добутку двох залежних подій А і В дорівнює добутку ймовірності однієї з них на умовну ймовірність другої, яка знайдена з припущенням того, що перша подія настала, тобто
![]()
8.Формула повної ймовірності та формула Байєса
Формула повної ймовірності:
Нехай в умовах експерименту
подія
![]() з'являється
спільно з однією з групи несумісних
подій (гіпотез)
з'являється
спільно з однією з групи несумісних
подій (гіпотез)
![]() ,
що утворюють повну групу
,
що утворюють повну групу
![]() ,
відомі або можливо встановити апріорні
ймовірністі
,
відомі або можливо встановити апріорні
ймовірністі
![]() кожної
з гіпотез та умовні ймовірності
кожної
з гіпотез та умовні ймовірності
![]() події
за
умови, що здійснилася та або інша
гіпотеза, тоді ймовірність події
визначається
за формулою повної ймовірності:
події
за
умови, що здійснилася та або інша
гіпотеза, тоді ймовірність події
визначається
за формулою повної ймовірності:
![]()
де
![]() –
ймовірність гіпотези
–
ймовірність гіпотези
![]() ;
–
умовна ймовірність події
при
виконанні гіпотези
.
;
–
умовна ймовірність події
при
виконанні гіпотези
.
Формула Байєса: Нехай гіпотези
утворюють повну групу несумісних подій
(
)
і нехай подія
відбувається обов'язково з однією з
гіпотез
![]() .
Нехай подія
відбулася,
тоді ймовірність того, що вона відбулася
саме за умови
визначається формулою:
.
Нехай подія
відбулася,
тоді ймовірність того, що вона відбулася
саме за умови
визначається формулою: