1. недиагональный элемент равен алгебраической сумме сопротив-лений ветвей, одновременно входящих в контуры и . Слагаемое этой сум-мы будет положительным, если направления обхода контуров и в пределах данной ветви совпадают, и отрицательным, если не совпадают. Если контуры и не имеют общих ветвей, то элемент . Матрица является симметричной, поэтому ;

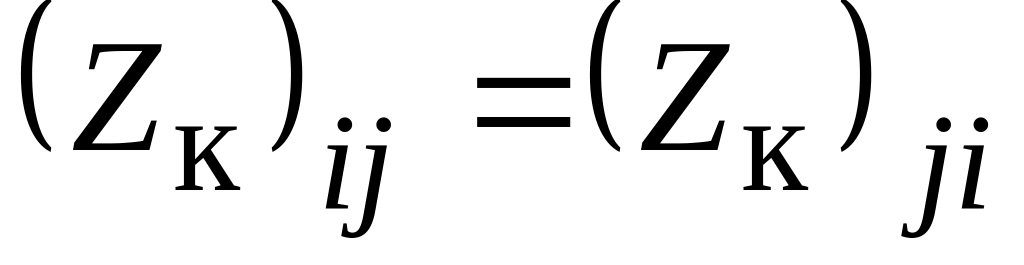2. Диагональный элемент равен сумме сопротивлений ветвей, образующих контур .

Для графа схемы замещения с системой базисных контуров, изображенных на рис. 1, имеем:

. (48)

В этом случае контурное уравнение состояния в развернутом виде есть:

. (49)

Контурное уравнение состояния (46) можно решить относительно токов в хордах путем обращения матрицы :

. (50)

Зная , можно опрделить токи во всех ветвях схемы по формуле (40). Затем определяются падения напряжений в ветвях согласно закону Ома (42) и абсолютные узловые напряжения по формуле:

, (51)

где - напряжение балансирующего узла. Наконец, мощности в узлах можно найти по формуле (29).

РАСЧЕТ ПАРАМЕТРОВ УСТАНОВИВШЕГОСЯ РЕЖИМА

МЕТОДОМ УЗЛОВЫХ НАПРЯЖЕНИЙ

Узловые уравнения основаны на уравнениях первого закона Кирхгофа и закона Ома. Преимущество их состоит в том, что они не требуют определения второй матрицы инциденций и их применение позволяет сократить порядок решаемой системы уравнений до числа независимых узлов по сравнению с использованием системы обобщенных уравнений состояния, имеющей порядок, равный числу ветвей схемы . Поэтому метод узловых напряжений широко применяется при расчетах установившихся режимов сложных электрических систем.

Подставляя матричное уравнение закона Ома

(53)

в выражение, связывающее падения напряжений в ветвях с относительными узловыми напряжениями ,

, (54)

получим:

. (55)

Матрица сопротивлений ветвей - квадратная и неособенная, поэтому

. (56)

Подставляя (56) в уравнение первого закона Кирхгофа

, (57)

получаем:

(58)

или

. (59)

Величина

(60)

представляет собой квадратную матрицу порядка , называемую матрицей узловых проводимостей. Введем величину

, (61)

которая представляет собой столбец, содержащий элементов и называемый столбцом «приведенных» токов в узлах. При отсутствии ЭДС в ветвях ( ), что характерно для многих схем замещения реальных электрических систем, . В результате введенных обозначений получим систему узловых уравнений в матричной форме:

. (62)

Формирование узловых уравнений сводится к определению матрицы узловых проводимостей . В случае, когда матрица сопротивлений ветвей является диагональной, произвольный элемент матрицы можно записать в виде:

,. (63)

где и - элементы первой матрицы инциденций .

Из выражения (63) вытекают следующие правила составления матрицы узловых проводимостей в случае, когда матрица имеет диагональную форму:

1. недиагональный элемент 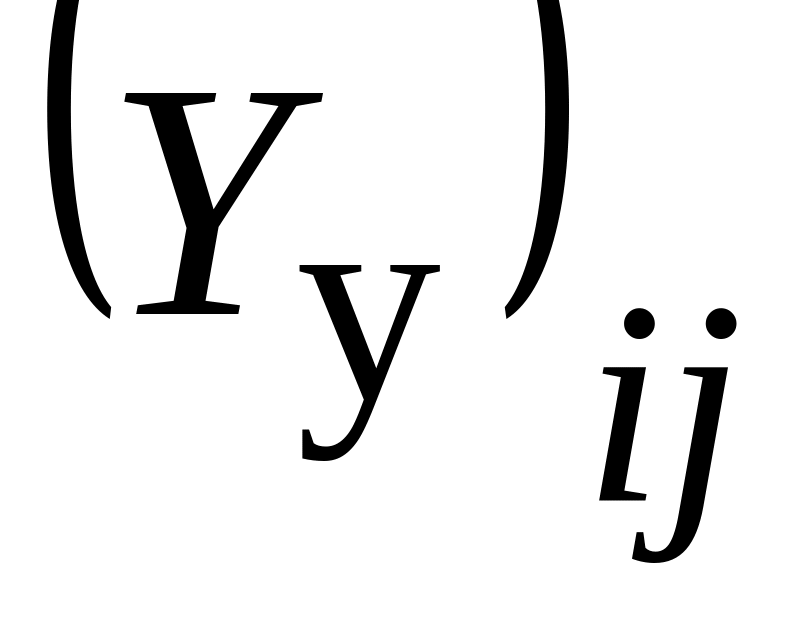называется взаимной проводимостью узлов и . Если между двумя узлами в схеме нет ветви, то соответствующая взаимная проводимость равна нулю. Если узлы и соединены одной ветвью с сопротивлением , то

. (64)

Матрица является симметричной, поэтому ;

2. диагональный элемент 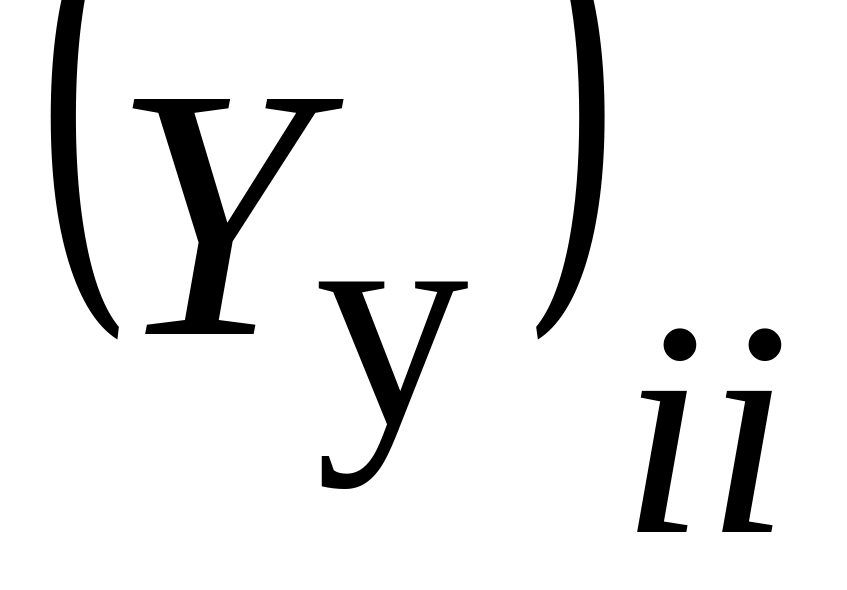называется собственной проводимостью узла и равен сумме проводимостей всех ветвей, соединенных с узлом . Если таких ветвей нет, то собственная проводимость узла равна сумме всех взаимных проводимостей , взятой с обратным знаком. Пусть, например, с узлом соединено ветвей, тогда

. (65)

Для графа схемы замещения, изображенного на рис. 1, имеем:

. (66)

Система узловых уравнений для этого графа имеет вид:

. (67)

Решив уравнение (62) относительно узловых напряжений

, (68)

можно затем рассчитать падения напряжения на ветвях схемы по формуле (54) и токи в ветвях по выражению (56). Абсолютные узловые напряжения находятся из соотношения:

, (69)

где - напряжение балансирующего узла. Наконец, мощности в узлах равны:

. (70)