Расчет параметров установившегося режима методом контурных токов

Последовательность расчета параметров установившегося режима электрической системы характеризуется тем, что при определении токов в ветвях решается система уравнений порядка , где - число ветвей, равное сумме числа независимых узлов и числа независимых контуров . Существует два способа понижения порядка системы уравнений. Первый сводит обобщенное уравнение состояния (20) к системе из узловых уравнений, основанных на первом законе Кирхгофа и законе Ома, а второй сводит обобщенное уравнение состояния к системе из контурных уравнений, базирующихся на втором законе Кирхгофа и законе Ома.

Контурные уравнения состояния можно получить следующим образом. Выделяя в матрице блоки, соответствующие ветвям дерева и хордам, уравнение первого закона Кирхгофа

(30)

можно представить в виде:

, (31)

где и - столбцы токов в ветвях дерева и хордах соответственно. Отсюда следует, что

(32)

и

. (33)

При выборе системы независимых базисных контуров и справедливо соотношение

, (34)

при транспонировании которого получаем

. (35)

Поэтому

(36)

и

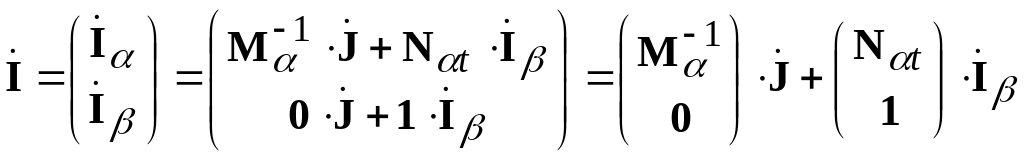. (37)

Введем обозначение:

. (38)

Здесь - прямоугольная матрица размерностью , а - нулевая прямоугольная матрица размерностью .

Так как

, (39)

то выражение (37) преобразуется к виду:

. (40)

Матричное уравнение второго закона Кирхгофа

(41)

с учетом закона Ома

(42)

и соотношения (40) приводит к выражению:

, (43)

где - столбец контурных ЭДС, а величина

(44)

представляет собой квадратную матрицу порядка , которая называется матрицей контурных сопротивлений. Удобно также ввести величину

, (45)

которую можно назвать столбцом «приведенных» контурных ЭДС. При отсутствии задающих токов в узлах, что отвечает схеме замещения, в которой электростанции представлены источниками напряжения, а нагрузки - сопротивлениями, и .

С учетом обозначений (44) и (45) система взаимно независимых контурных уравнений в матричной форме (43) принимает простой вид:

. (46)

Формирование контурных уравнений сводится к определению матрицы контурных сопротивлений . В случае, когда матрица сопротивлений ветвей является диагональной, произвольный элемент матрицы можно записать в виде:

, (47)

где и - элементы второй матрицы инциденций. Из выражения (47) вытекают следующие правила составления матрицы контурных сопротивлений в случае, когда матрица имеет диагональную форму: