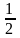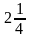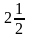Правительство Российской Федерации

Пермский филиал федерального государственного автономного образовательного учреждения высшего профессионального образования

«Национальный исследовательский университет «Высшая школа экономики»

Вечерне-заочный факультет экономики и управления

контрольная РАБОТА

По дисциплине «Методы оптимальных решений»

Студент группы Э-12Уз

Антонов Алексей Владимирович

________________________

подпись

Преподаватель

Чадов Алексей Леонидович

________________________

подпись

Пермь 2014

Вариант 8

Задание №1

Решить задачу линейного программирования графически. Записать двойственную к ней и решить её графически.

Решение:

1. Решим задачу графически:

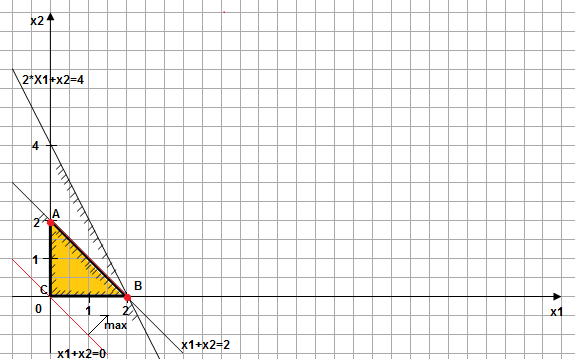
Построим область допустимых решений, ограниченную прямыми:

1. x₁+x₂ = 2, точки (2; 0) и (0; 2).

2. 2x₁+x₂=4, точки (0; 4) и (2; 0).

Штриховкой выделим ту полуплоскость, которую определяет соответствующее неравенство, находим область пересечений всех неравенств в первой четверти, т.к. Получаем треугольную область ABC.

Строим линию уровня целевой функции x₁+x₂=0. Находим направление максимума и перемещаем линию уровня целевой функции до тех пор, пока не выйдем из полученной области.

Видим, что на выходе из области уровень целевой функции совпадает с отрезком АВ, поэтому любая точка принадлежащая данному отрезку является решение задачи, при этом целевая функция принимает максимальное значение, равное двум.

2. Запишем двойственную задачу

Задача уже имеет стандартный вид, т.к. целевая функция стремится к максимуму, а все неравенства имеют вид .

Так как исходная задача была на максимум, двойственная задача будет на минимум, причем коэффициенты при переменных в целевой функции соответствуют правым частям ограничений, число переменных равно числу ограничений исходной задачи и равно двум.

Целевая функция двойственной задачи:

Строим ограничения, транспортируя матрицу коэффициентов в ограничениях.

Так как все переменные были неотрицательны, все ограничения будут иметь знаки . Правые части ограничений – это коэффициенты при переменных в исходной целевой функции.

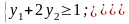
Первое и второе ограничения исходной задачи имеют знак , поэтому соответствующие двойственные переменные неотрицательны.

Итак, мы составили двойственную задачу:

3. Решим двойственную задачу графическим методом.

Построим область допустимых решений, ограниченную прямыми:

1. , точки (1; 0) и (0; 0,5).

2. , точки (0; 1) и (1; 0).

Штриховкой выделим ту полуплоскость, которую определяет соответствующее неравенство, находим область пересечений всех неравенств в первой четверти, т.к. . Получаем неограниченную область ABCD.

Строим линию уровня целевой функции =0. Находим направление минимума и перемещаем линию уровня целевой функции до тех пор, пока не выйдем из полученной области.

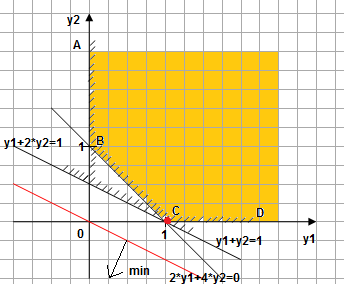
Видим, что на выходе из области уровень целевой функции совпадает с точкой С, в которой y₁=1, а y₂=0. Целевая функция в данной точки принимает значение 2.

Задание №2

Мебельная фабрика выпускает журнальные столики двух видов: «люкс» и «стандарт». Для их производства используется два вида сырья: вагонка и бруски. Для производства одного столика «стандарт» расходуется 1 упаковка вагонки и 1 погонный метр (п.м.) брусков, а для производства одного столика «люкс» используется 2 упаковки вагонки и 1 п.м. брусков. Цена одного столика «стандарт» 3 тыс.руб., а «люкс» – 4 тыс.руб. В распоряжении фабрики 10 упаковок вагонки и 8 п.м. брусков.

У фирмы также есть возможность продать имеющиеся у неё ресурсы (полностью или частично) по рыночным ценам р₁ тыс. руб. за 1 упаковку вагонки и р₂ тыс. руб. за 1 п.м. брусков

Определить оптимальный объем производства, максимизирующий прибыль от производства и продажи ресурсов, для каждого из 5 случаев цен (р₁, р₂) на ресурсы:

Цена	Случай 1	Случай 2	Случай 3	Случай 4	Случай 5
р1
р2

Этапы решения задачи:

1) Найти графические решения исходной и двойственной задач.

2) Сравнить двойственные оценки и цены на ресурсы. Сделать выводы.

3) Найти выручку от продажи всех ресурсов по предложенным ценам и альтернативные издержки производства обоих товаров. Сравнить альтернативные издержки с ценой продажи товаров. Сделать вывод о выгодности производства товаров.

4) Используя результаты п. 3, найти оптимальный план производства, максимизирующий прибыль от производства и продажи ресурсов. Найти оптимальное значение прибыли.

5) Для систематизации произведенных расчет занести найденные значения в таблицу.

6) Записать функцию прибыли, используя экономические соображения. Получить тот же результат математически.

7) Используя функцию прибыли проверить найденный в п. 4 оптимальный план производства, решив задачу графически.

Решение:

Составим математическую модель исходной задачи:

Решим её графическим методом по аналогии с предыдущим заданием.

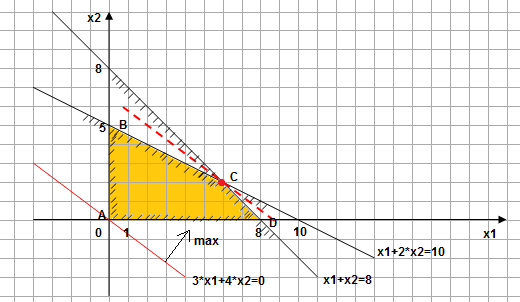
Видим, что целевая функция покидает область решений ABCD в точке C, где и достигает своего максимума.

Чтобы найти координаты этой точки необходимо решить систему уравнений:

.

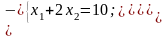Таким образом, решением задачи является (6; 2), при значении целевой функции 3*6+4*2 = 26.

Запишем двойственную задачу:

Решим двойственную задачу графическим методом.

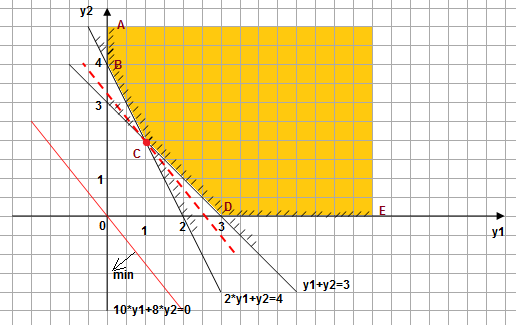
Видим, что целевая функция достигает своего минимума в точке С, определим её координаты решив систему уравнений:

.

Решение двойственной задачи: (1; 2) при минимальном значении целевой функции 10*1+8*2 = 26.

Случай 1

Цены на ресурсы ( ; ). Цена первого вида ресурсов (вагонки) меньше чем, её двойственная оценка, а второго вида ресурсов (брусков) больше таковой.

При таких значениях цен ресурсов целевая функция двойственной задачи (т.е. выручка от продажи всех видов ресурсов) примет значение 10*0,5+8*2,75 = 27, что больше, а значит является менее прибыльным для предприятия при производстве столиков, но более прибыльным при продаже ресурсов.

Альтернативные издержки при производстве столиков «стандарт» составят 0,5+2,75 = 3,25, что выше цены реализации данного вида товара. Такие столики производить не выгодно.

Альтернативные издержки при производстве столиков «люкс» составят 2*0,5+2,75 = 3,75, что меньше, чем цена реализации данного товара, а значит производить столики данного вида выгодно.

Если будет производится, только второй вид столиков, то максимально возможное их число для производства составляет 5 шт., т.к. затраты вагонки на данный вид столиков составляют 2 упаковки, а их запас ограничивается 10 упаковками.

Отсюда оптимальный план производства (0; 5).

При этом, доход от продажи столиков и оставшегося бруска составит: 5*4 + 3*2,75 = 28,25 тыс. руб. Тогда прибыль составит 28,25-27 = 1,25 тыс. руб.

Функция прибыли будет составляться из прибыли (убытка) от продажи обоих видов столиков. Прибыль от конкретного вида столика, определяется как произведение количества столиков на разницу между ценой и себестоимостью:

(3-3,25)*х₁ + (4-3,75)*х₂ = -0,25х₁ + 0,25х_2.

Выведем эту же функцию математически:

3х₁ + 4х₂ + 0,5*(10– x₁ – 2*x₂) + 2,75*(8– x₁ – x₂) – 27 =

= 3х₁ + 4х₂ + 0,5*10– 0,5 x₁ – 0,5*2*x₂ + 2,75*8– 2,75*x₁ – 2,75*x₂) – 27 =

= (3х₁ – 0,5 x₁ – 2,75*x₁) + (4х₂ – 0,5*2*x₂ – 2,75*x₂)+ (5+ 22 – 27) =

= -0,25х₁ + 0,25х_2..

Используя функцию прибыли проверим найденный оптимальный план производства, решив задачу графически:

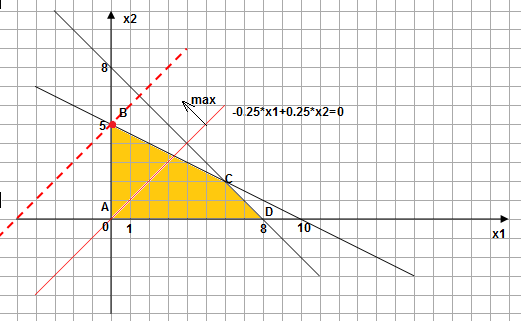
Функция прибыли приходит в максимум в точке B с координатами (0; 5). Таким образом, найденый ранее оптимальный план определен верно.