Определение

Другими словами, множество  называется выпуклой, если:

То есть, если множество X вместе с любыми двумя точками, которые принадлежат этому множеству, содержит отрезок, их соединяющий:

.

Точка выпуклого множества, которая не является внутренней ни для какого ненулевого отрезка, целиком принадлежащего этому множеству, называется его крайней точкой. У г л о в ы м и ( крайними) точками выпуклого множества называются точки, не являющиеся выпуклой комбинацией двух различных точек этого множества.

Многогранник называется выпуклым, если он весь лежит по одну сторону от плоскости любой его грани; тогда грани его тоже выпуклы. Выпуклый Многогранник разрезает пространство на две части — внешнюю и внутреннюю. Внутренняя его часть есть выпуклое тело. Обратно, если поверхность выпуклого тела многогранная, то соответствующий Многогранник — выпуклый.

ВЫПУКЛЫЙ МНОГОГРАННИК - выпуклая оболочка конечного числа точек в евклидовом пространстве Eⁿ. Такой Выпуклый многогранник есть ограниченное непустое пересечение конечного числа замкнутых полупространств. Бесконечным Выпуклым многогранником называют пересечение конечного числа замкнутых полупространств, содержащее по крайней мере один луч, причем уславливаются пространство   также считать В. м. В этом смысле В. м. есть замкнутая выпуклая оболочка конечного числа точек и лучей. Размерностью В. м. наз. минимальную размерность содержащего его пространства  В. м. - частный вид выпуклого множества. Как пересечение полупространств В. м. описывается системой линейных неравенств и может быть исследован алгебраическими средствами.

Рассмотрим некоторые свойства выпуклых многогранников.

Свойство 1. В выпуклом многограннике все грани являются выпуклыми многоугольниками.

Свойство 2. Выпуклый многогранник может быть составлен из пирамид с общей вершиной, основания которых образуют поверхность многогранника.

Свойство 3. Выпуклый многогранник лежит по одну сторону от плоскости каждой своей грани.

Свойство 4. В любом выпуклом многограннике найдется грань с числом ребер меньшим или равным пяти.

24. Графический метод решения ЗЛП состоит из следующих этапов.

1. Строится многоугольная область допустимых решений ЗЛП – ОДР,

2. Строится вектор-градиент ЦФ в какой-нибудь точке Х₀ принадлежащей ОДР –

.

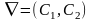3. Линия уровня C₁x₁+C₂x₂ = а (а–постоянная величина) - прямая, перпендикулярная вектору –градиенту – передвигается в направлении этого вектора в случае максимизации f(x_1,x₂) до тех пор, пока не покинет пределов ОДР. Предельная точка (или точки) области при этом движении и является точкой максимума f(x_1,x₂).

4. Для нахождения ее координат достаточно решить два уравнения прямых, получаемых из соответствующих ограничений и дающих в пересечении точку максимума. Значение f(x_1,x₂), найденное в получаемой точке, является максимальным.

При минимизации f(x_1,x₂) линия уровня перемещается в направлении, противоположном вектору-градиенту. Если прямая при своем движении не покидает ОДР, то соответствующий максимум или минимум f(x_1,x₂) не существует.

Если линия уровня параллельна какому-либо функциональному ограничению задачи, то оптимальное значение ЦФ будет достигаться в любой точке этого ограничения, лежащей между двумя оптимальными угловыми точками, и, соответственно, любая из этих точек является оптимальным решением ЗЛП.

25.Виды областей допустимости значений и нахождение оптимальных точек при графическом решении ЗЛП. Альтернативный оптимум.

ОДЗ может быть а) выпуклым многоугольником,

Единственность опт.решения.В этом случае опорная изоцель имеет одз только 1 общую точку.

б) выпуклой много-угольной неограниченной областью,

Отсутствие оптимального решения.ЗЛП не имеет оптимального решения,т.к. целевая ф-ция не ограничена сверху(если требуется найти мах цел ф-ци) ил снизу (если найти мин.) В этом случае линия уравнения не является опорной к одз при решении задачи на мах.

в) точкой,

Если ОДЗ состоит из 1 точки, то в этой точке Z принимает свое макс. Мин значение.

г) пустым множеством

ЗЛП не имеет решения,т.к. система ограничений противоречива, т.е. ОДЗ =Ǿ

Альтернативный оптимум.Множество оптим решений)

В этом случае опорная изоцель совпадает с одной из сторон многоугольника решений.В данном случае цел ф-ция достигает своего макс.значения в любой точке отрезка [A;B]: X_max Є [A;B] и записывается в виде выпуклой комбинации X_max=λ*А +(1-λ)*В, 0≤ λ ≤1

При решении задач ЛП симплексным методом критерием оптимальности является условие ∆j > 0 для задач на максимум и условие ∆j < 0 для задач на минимум. Если на каком-то шаге окажется, что хотя бы одна оценка свободной переменной ∆j = 0, а все остальные ∆j > 0 для задач на максимум ( ∆j < 0 для задач на минимум), то, приняв в качестве ключевого столбца столбец, где ∆j = 0, и найдя новое оптимальное решение, заметим, что значение целевой функции при этом не изменится. В этом случае задача имеет альтернативный оптимум.

Критерием альтернативного оптимума при решении задач симплексным методом является равенство нулю хотя бы одной оценки свободной переменной (∆j = 0).

26. Решение ЗЛП заданных в канонической форме при условии,что n-m=2

Пусть задача в канон форме имеет n переменных и m ограничений.задача может быть решена граф.методом,если n-m=2

Выделяем методом Жордана-Гаусса базисные переменные. Выражая целевую функцию через свободные переменные и отбрасывая базисные переменные из полученной системы ограничений с учетом их неот рицательности, получаем ЗЛП с двумя переменными. Решая эту задачу, находим х5, х6 и Zmax. Максимальное значение целевая функция принимает в точке D, находим её координаты. И находим значения остальных (базисных) переменных.