13. Модель международной торговли.
С
помощью модели международной торговли
можно определить, какими должны быть
соотношения бюджетов стран, торгующих
между собой, что бы торговля была
взаимовыгодной. Рассмотрим модель
международной торговли, в кот. участвуют
n
стра6. Обозначим:
-
национальный доход і-й
страны;
– доля национального дохода j-й
страны, которую она расходует на закупку
товаров і-й
страны;
- общая выручка от внутренней и внешней
торговли для і-й
страны. Предположим, что каждое гос-во
расходует весь свой нац. доход на закупку
товаров внутри страны и на импорт из
других стран. Это означает, что:
.
Матрица
А, элементами которой явл. коэффициенты
,
называется структурной матрицей
торговли. Сумма элементов каждого
столбца этой матриц е = 1. Предположим,
что в течении определенного фиксированного
промежутка времени структура международной
торговли не меняется, а национальные
доходы торгующих стран могут измениться.
Требуется определить эти нац. доходы,
чтобы международ. торговля осталась
сбалансированной, т.е., что бы сумма
платежей всех гос-в была равна суммарной
выручке от внешней и внутренней торговли.
Для любой страны выручка от внут. и
внеш. торговли составит:
В
сбалансированной системе международ.
торг. не должно быть дефицита, т.е. у
каждой страны выручка от торговли
должны быть не меньше ее нац. дохода
.
Последнее неравенство справедливо
только в том случае, когда
т.е. у всех торгующих стран выручка от
внеш. и внут. торговли должны совпадать
с нац. доходом. В матричной записи это
означает, что имеет место равенсво
АХ=Х, где А – структурная матрица
международ. торговле, а Х- вектор нац.
доходов. Вектор Х явл. собственным
вектором структурной матрицы торговли
А, а соответствующее собственное
значение равно 1. Отсюда следует, что
баланс в международ. торговле будет
достигнут, если единица явл. собственным
числом структурной матрицы международ.
торговли, а вектор нац. доходов торгующих
стран—собственным вектором, отвечающим
этому единичному собственному значению.
14. Общая форма модели задач линейного программирования и ее особенности.
Найти
значения переменных Х=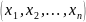
,
которые удовлетворяли бы условиям
(1.1)
и
обеспечивали бы max
или min
целевой функции
(1.2)
Дополнительно
налагаются условия неотрицательности
переменных
(1.3) или указываются диапазоны их
изменения
X1-произвольного знака, Х2-произвольного знака, Х3-произвольного знака.
,
,
.
На каждую переменную налагается одно
из написанных ограничений. Решение,
которое удовлетворяет условию (1.1)
называется возможным, условиям (1.1),
(1.3) – допустимым или планом. Решение,
которое удовлетворяет условиям (1.1),
(1.2) (1.3) называется отптипальным.
15. Стандартная форма модели задач линейного программирования и ее особенности.
Стандартная форма ЗЛП в матричном виде записывается следующим образом:
Z=CX
min
или
Z=CX
max
AX
B,
AX
B
X 0 X 0
Чтобы свести задачу к стандартному виду, необходимо:
1. Некоторые неравенства умножают на -1, чтобы поменять знак неравенства;
2.
Чтобы перейти от нахождения max
к нахождению
min
или наоборот, необходимо сделать замену
;
3. Сделать переменные неотрицательными;
4.
Уравнение
можно
заменить системой неравенств
Если ограничения записаны в виде системы уравнений, то методом Жордана-Гаусса находят одно общее решение системы и подставляют выражения каждой базисной переменной в целевую функцию. Отбрасывая базисные переменные из каждого уравнения общего решения, учитывая их неотрицательность, превращают уравнение в неравенства и получают ЗЛП относительно свободных переменных в стандартной форме. При этом кол-во переменных уменьшается.