1. Математические модели позволяют определять оптимальные значения неизвестных параметров экономических систем, что является важным в процессе принятия решений. Математическое прогр. дает аппарат, позволяющий оптимизировать процесс отбора лучших вариантов планов в процессе управления в экономических системах.
Используется в матстатистике, оптимизационные методы, методы экономической кибернетики, эксперементальные задачи.
При изучении сложных процессов и явлений в экономике часто используется моделирование – определенное отображение рассматриваемых характеристик изучаемого объекта. суть его: изучаемое явление воспроизводится в эксперементальных условиях с помощью модели в другом временном и пространственном масштабе. Математическое моделирование – наиболее совершенный и эффективный способ получения информации о исследуемом объекте. Это мощное средство анализа в экономике. результаты исследования с помощью моделей будут иметь практический интерес тогда. когда построенная модель будет достаточно адекватной рассматриваемому явлению.
2. Математическое Программирование - математическая дисциплина, посвященная теории и методам решения задач о нахождении экстремумов функций на множествах конечномерного векторного пространства, определяемых линейными и нелинейными ограничениями (равенствами и неравенствами).
К мат. программированию относят ряд разделов, основыне из которых – следующие:
1. Линейное программирование – задачи, в которых неизвестные переменные входят в мамтематическое соотношение в 1 степени.
2. Нелинейное программирование – задачи, в которых целевая функция или ограничения могет быть нелинейными.
3. Динамическое – задачи, в которых процесс решения можно разбить на несколько этапов.
4. Целочисленное – задачи, в которых неизвестные переменные могут принимать только целые значения.
5. Стохастическое – задачи, в которых содержатся случайные пересенные в целевой функции или ограничениях.
6. Параметрическое – задачи, в которых коэффициенты, при неизвестных переменных в цел. функции или ограничених зависят от некотрых параметров.
Для решения задач мат. программирования сложно использовать классические методы нахождения экстремум, т.к. в таких задачах цел. функция достигает своего экстремального значения на границе области допустимых значений неизвстных переменных, а производные в граничных точках не существуют. Полный перебор допустимых точек невозможен из-за их большого количества.
3. Математи́ческая моде́ль — это математическое представление реальности.
Все естественные и общественные науки, использующие математический аппарат, по сути занимаются математическим моделированием: заменяют реальный объект его математической моделью и затем изучают последнюю.
Математические модели, используемые в экономике, можно разделить на классы в зависимости от особенностей моделируемых объектов, цели и методов моделирования.
Макроэкономические модели предназначены для описания экономики как единого целого. Основными характеристиками, используемыми при анализе, являются ВНП, потребление, инвестиции, занятость, количество денег и др.
Микроэкономические модели описывают взаимодействие структурных и функциональных составляющих экономики или поведение одной из составляющих в среде остальных. Основные объекты приложения моделирования в микроэкономике – это предложение, спрос, эластичность, издержки, производство, конкуренция, потребительский выбор, ценообразование, теория монополии, теория фирмы и др.
По характеру модели могут быть теоретическими (абстрактными), прикладными, статическими, динамическими, детерминированными, стохастическими, равновесными, оптимизационными, натурными, физическими.
Теоретические модели позволяют изучать общие свойства экономики, исходя из формальных предпосылок с использованием метода дедукции.
Прикладные модели позволяют оценивать параметры функционирования экономического объекта. Они оперируют числовыми знаниями экономических переменных. Чаще всего в этих моделях используют статистические или фактические наблюдаемые данные.
Равновесные модели описывают такое состояние экономики как системы, при котором сумма всех действующих на нее сил равна нулю.
Оптимизационные модели оперируют с понятием максимизации полезности, результатом которой является выбор поведения, при котором сохраняется состояние равновесия на микроуровне.
Статические модели описывают мгновенное состояние экономического объекта или явления.
Динамическая модель описывает состояние объекта как функцию времени.
Стохастические модели учитывают случайные воздействия на экономические характеристики и используют аппарат теории вероятностей.
Детерминированные модели предполагают наличие между изучаемыми характеристиками функциональной связи и, как правило, используют аппарат дифференциальных уравнений.
Натурное моделирование проводится на реально существующих объектах при специально подобранных условиях, например, эксперимент, проводимый во время производственного процесса на действующем предприятии, отвечающий при этом задачам самого производства.
4. Общая постановка задач.
Общая задача – определение оптичального значения целевой функции, причем значения переменных должны принадлежать области допустимых значений. Математическое определение оптимально решения – нахождение экстремума функции многих переменных.
Z = f(X1, X2,..., Xn)
в заданной области изменения этих переменных
gi(X1,X2,..., Xn)Ribi
i=(1,2,...,m)
Ri – один из знаков,≤, =, ≥.
5. Задача “об оптимизации плана выпуска продукции”. Экономическая постановка и построение математической модели задачи.
Пусть
предприятием выпускается n
видов продукции
,
,…,
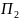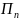из m
видов сырья
,
,…,
.
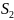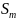Известны
запасы сырья
,
,…,
,
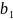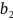расходы
(i=1,m;
j=1,n)
единиц i-го
сырья на единицу j-й
продукции и цены
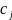реализации единицы продукции j-го
вида. Составим математическую модель
задачи таким образом, чтобы определить
сколько единиц продукции каждого вида
необходимо выпускать предприятию,
чтобы доход от реализации был максимальным.
Введем
переменные:
(j=1,n)
– количество единиц продукции j-го
вида, которое предполагается выпускать.
Тогда
-
стоимость всей выпускаемой продукции
j-го
вида,Z=
+
+…+
-
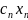стоимость всей выпускаемой
продукции.
+
+…+
-
затраты
i-го
вида сырья на всю выпускаемую продукцию.
Затраты не могут превышать запаса
,
поэтому
+
+…+
≤
.Такие
условия необходимо записать по всем
видам сырья. По смыслу задачи все
переменные должны быть неотрицательными.
Математическая модель задачи будет следующей:
Z= + +…+ →max
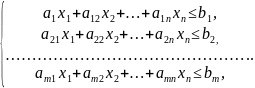
≥0 (j=1,n)
6. Задача “о рационе”. Экономическая постановка и построение математической модели.
Для
откорма животных используют n
видов кормов
,
,…,
.
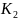Для рационального откорма каждое
животное должно ежедневно получать не
менее чем
,
,…,
единиц питательных веществ
,
,…,
соответсвенно Известно содержание
i-ых
ед. питательных веществ в одном килограмме
j-го
корма и цена
(j=1,n)
одного килограмма корма. Найти оптимальный
дневной рацион, чтобы его стоимость
была минимальной при необходимой
питательности.
Введем переменные Z – цена ежедневного рациона, (j=1,n) – количество корма j-го вида в рационе. Тогда - стоимость корма j-го вида в рационе, Z= + +…+ - стоимость всего корма, включенного в рацион, + +…+ – количество питательных веществ i-го вида в рационе. Количество питательных веществ i-го вида в рационе долино бать не менше нормы , поэтому + +…+ ≥ . По смыслу задачи все переменные должны быть неотрицательными.
Математическая модель:
Z= + +…+ →min
≥0 (j=1,n)
7. “Транспортная задача”. Экономическая постановка и построение математической модели задачи.
Пусть
имеется m
поставщиков
,
,…,
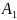с запасами однородного груза
,
,…,
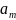и n
потребителей
,
,…,
с потребностями этого груза
,
,…,
.
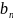При этом груз измеряется в одних и тех
же единицах (тонны, штуки, вагоны и
т.д.). Задача называется закрытой, если
+
+…+
=
+
+…+
.
Если
+
+…+
≠
+
+…+
,
то задача называется открытой (тогда
вводим фиктивного поставщика или
потребителя).
Рассмотрим закрытую задачу.
Известны
цены (тарифы) перевозок
единицы груза от i-го
поставщика к j-му
потребителю. Необходимо составить
такой план перевозки груза от каждого
поставщика каждому потребителю, при
котором вывозится весь груз, удовлетворяются
все потребности, и суммарная стоимость
перевозки минимальна.
Обозначим
через
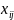-количество
груза, который планируется перевозить
от i-го
поставщика к j-му
потребителю, Z-
общая стоимость перевозок.
Математическая модель закрытой задачи имеет вид:
Z=
+
+…+
=
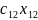→min
– стоимость перевозок груза
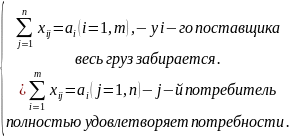
≥0