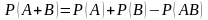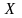∑ ∑ ∑ ∑ ∑ ∑ ∑
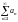 -
қатарының жинақты болуының қажетті
шартын көрсетіңіз
-
қатарының жинақты болуының қажетті
шартын көрсетіңіз

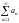 қатарының
жинақсыз болуының жеткілікті шартын
көрсетіңіз
қатарының
жинақсыз болуының жеткілікті шартын
көрсетіңіз
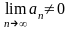
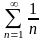 гармоникалық
қатары қандай болады?
гармоникалық
қатары қандай болады?
Жинақсыз
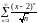 қатарының
жинақтылық облысын табыңыз
қатарының
жинақтылық облысын табыңыз

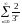 қатарының
қосындысын табыңыз
қатарының
қосындысын табыңыз
3
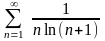 қатарды
жинақтылыққа зерттеңіз
қатарды
жинақтылыққа зерттеңіз
Жинақсыз
 қатардың
жинақтылық облысын
табыңыз
қатардың
жинақтылық облысын
табыңыз
[-3, 3)
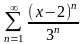 қатардың
жинақтылық облысын
табыңыз
қатардың
жинақтылық облысын
табыңыз
(-1,5)
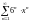 қатардың
жинақтылық радиусын табыңыз
қатардың
жинақтылық радиусын табыңыз
1/6
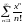 қатардың
жинақтылық радиусын табыңыз
қатардың
жинақтылық радиусын табыңыз
+
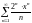 қатардың
жинақтылық облысын
табыңыз
қатардың
жинақтылық облысын
табыңыз

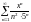 қатардың
жинақтылық облысын
табыңыз
қатардың
жинақтылық облысын
табыңыз
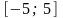
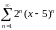 қатардың
жинақтылық облысын
табыңыз
қатардың
жинақтылық облысын
табыңыз
(4,5; 5,5)
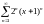 қатардың
жинақтылық облысын
табыңыз
қатардың
жинақтылық облысын
табыңыз
(-1,5; -0,5)
 қатарын
жинақтылыққа зерттеңіз
қатарын
жинақтылыққа зерттеңіз
Жинақсыз
 қатарын
жинақтылыққа зерттеңіз
қатарын
жинақтылыққа зерттеңіз
Жинақсыз
 қатарының
жинақтылыққа зерттеңіз
қатарының
жинақтылыққа зерттеңіз
Жинақты
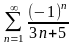 қатардың
төртiншi мүшесiн табыңыз
қатардың
төртiншi мүшесiн табыңыз
1/17
 қатардың
төртiншi мүшесiн табыңыз
қатардың
төртiншi мүшесiн табыңыз
1/16
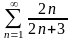 қатардың
бесінші мүшесiн табыңыз
қатардың
бесінші мүшесiн табыңыз
10/13
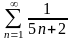 қатарының
алғашқы екі мүшесінің қосындысын
табыңыз
қатарының
алғашқы екі мүшесінің қосындысын
табыңыз
19/84
 қатарының
алғашқы екі мүшесінің қосындысын
табыңыз
қатарының
алғашқы екі мүшесінің қосындысын
табыңыз
9/8
 қатарының
алғашқы екі мүшесінің қосындысын
табыңыз
қатарының
алғашқы екі мүшесінің қосындысын
табыңыз

 қатарының
алғашқы екі мүшесінің қосындысын
табыңыз
қатарының
алғашқы екі мүшесінің қосындысын
табыңыз

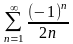 қатарының
үшінші және бесінші мүшелерінің
қосындысын табыңыз
қатарының
үшінші және бесінші мүшелерінің
қосындысын табыңыз

 қатарды
жинақтылыққа зерттеңіз
қатарды
жинақтылыққа зерттеңіз
абсолютті жинақты
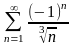 қатарды
жинақтылыққа зерттеңіз
қатарды
жинақтылыққа зерттеңіз
шартты жинақты
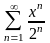 қатардың
жинақтылық радиусын табыңыз
қатардың
жинақтылық радиусын табыңыз
2
 қатарын
жинақтылыққа зерттеніз
қатарын
жинақтылыққа зерттеніз
Жинақты
 қатарды
жинақтылыққа зерттеңіз
қатарды
жинақтылыққа зерттеңіз
Жинақты
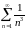 қатарды
жинақтылыққа зерттеңіз
қатарды
жинақтылыққа зерттеңіз
Жинақты
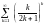 қатарын
жинақтылыққа зерттеңіз
қатарын
жинақтылыққа зерттеңіз
Жинақты
 қатарын
жинақтылыққа зерттеңіз
қатарын
жинақтылыққа зерттеңіз
жинақсыз
 қатарының
жинақтылық аралығын табыңыз
қатарының
жинақтылық аралығын табыңыз
(–2,2)
 қатарының
жинақтылық радиусын табыңыз
қатарының
жинақтылық радиусын табыңыз
1
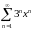 қатарының
жинақтылық радиусын табыңыз
қатарының
жинақтылық радиусын табыңыз
1/3
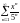 қатарының
жинақтылық радиусын табыңыз
қатарының
жинақтылық радиусын табыңыз
5
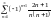 қатарының
қатарының
 және
және
 мүшелерінің қосындысын табыңыз
мүшелерінің қосындысын табыңыз
2/15
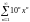 қатарының
жинақталу интервалын табыңыз
қатарының
жинақталу интервалын табыңыз

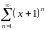 қатарының
жинақтылық интервалын табыңыз
қатарының
жинақтылық интервалын табыңыз
(-2; 0)
 қатарының
жинақтылық интервалын табыңыз
қатарының
жинақтылық интервалын табыңыз
(1; 3)
 қатарының
жинақтылық интервалын табыңыз
қатарының
жинақтылық интервалын табыңыз
(-1; 1)
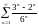 қатарының
қосындысын табыңыз
қатарының
қосындысын табыңыз
0,5
 қатарының
қосындысын табыңыз
қатарының
қосындысын табыңыз
0,5
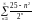 қатарының
бірінші және үшінші мүшелерінің айырымын
табыңыз
қатарының
бірінші және үшінші мүшелерінің айырымын
табыңыз
10
 қатарының
бірінші және үшінші мүшелерінің
қосындысын табыңыз
қатарының
бірінші және үшінші мүшелерінің
қосындысын табыңыз
17,25
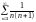 қатарының
қосындысын табыңыз
қатарының
қосындысын табыңыз
1
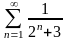 қатарының
алғашқы екі мүшесінің қосындысын
табыңыз
қатарының
алғашқы екі мүшесінің қосындысын
табыңыз
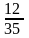
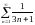 қатарының
алғашқы үш мүшесінің қосындысын табыңыз
қатарының
алғашқы үш мүшесінің қосындысын табыңыз
69/140
 дәрежелік
қатардың жинақтылық радиусын табыңыз
дәрежелік
қатардың жинақтылық радиусын табыңыз
4
 дәрежелік
қатардың жинақтылық радиусын табыңыз
дәрежелік
қатардың жинақтылық радиусын табыңыз
5/3
 қатарының
қосындысын табыңыз
қатарының
қосындысын табыңыз
5/6
 дәрежелік
қатардың жинақталу радиусын табыңыз
дәрежелік
қатардың жинақталу радиусын табыңыз
10
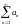 және
және
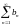 қатарлары жинақты, онда
қатарлары жинақты, онда
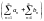 қатары туралы не айтуға болады
қатары туралы не айтуға болады
Жинақты
 қатарының
екінші және төртінші мүшелерінің
қосындысын табыңыз
қатарының
екінші және төртінші мүшелерінің
қосындысын табыңыз
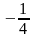
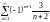 қатарының
екінші және үшінші мүшелерінің қосындысын
табыңыз
қатарының
екінші және үшінші мүшелерінің қосындысын
табыңыз
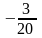
 қатарының
екінші және үшінші мүшелерінің қосындысын
табыңыз
қатарының
екінші және үшінші мүшелерінің қосындысын
табыңыз
-1
 қатарының
екінші және үшінші мүшелерінің қосындысын
табыңыз
қатарының
екінші және үшінші мүшелерінің қосындысын
табыңыз
13/27
 қатарының
алғашқы үш мүшесі мынадай:
қатарының
алғашқы үш мүшесі мынадай:
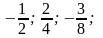
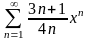 қатарының
жинақтылық радиусы тең
қатарының
жинақтылық радиусы тең
1
 ауыспалы
таңбалы қатары жинақты және оның
қосындысы
ауыспалы
таңбалы қатары жинақты және оның
қосындысы
 -
ке тең болса, онда
-
ке тең болса, онда
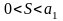
 дәрежелік
қатарының жинақтылық радиусы тең:
дәрежелік
қатарының жинақтылық радиусы тең:
1.
қатары қандай қатар деп аталады:
Гармоникалық.
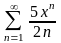 дәрежелік
қатарының жинақтылық радиусы тең:
дәрежелік
қатарының жинақтылық радиусы тең:
1
 қатарын
жинақтылыққа зерттеңіз
қатарын
жинақтылыққа зерттеңіз
Жинақты
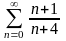 қатарының
жинақтылығын зерттеу үшін жинақтылықтың
мынадай белгісін қолданамыз:
қатарының
жинақтылығын зерттеу үшін жинақтылықтың
мынадай белгісін қолданамыз:
Жинақтылықтың қажеттілік белгісі
 қатарын
жинақтылыққа зерттеңіз
қатарын
жинақтылыққа зерттеңіз
Жинақсыз
 қатарын
жинақтылыққа зерттеңіз
қатарын
жинақтылыққа зерттеңіз
Жинақсыз
 қатарын
жинақтылыққа зерттеңіз
қатарын
жинақтылыққа зерттеңіз
Жинақсыз
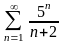 қатарын
жинақтылыққа зерттеңіз
қатарын
жинақтылыққа зерттеңіз
жинақсыз
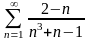 қатарын
жинақтылыққа зерттеңіз
қатарын
жинақтылыққа зерттеңіз
Жинақты
 қатарын
жинақтылыққа зерттеңіз
қатарын
жинақтылыққа зерттеңіз
Жинақсыз
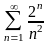 қатарын
жинақтылыққа зерттеңіз
қатарын
жинақтылыққа зерттеңіз
Жинақсыз
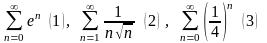 қатарларының
қайсысы жинақсыз қатар болады?
қатарларының
қайсысы жинақсыз қатар болады?
1.
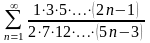 қатарын
жинақтылыққа зерттеңіз
қатарын
жинақтылыққа зерттеңіз
Жинақты
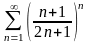 қатарын
жинақтылыққа зерттеңіз
қатарын
жинақтылыққа зерттеңіз
Жинақты
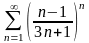 қатарын
жинақтылыққа зерттеңіз
қатарын
жинақтылыққа зерттеңіз
Жинақты
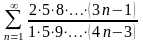 қатарын
жинақтылыққа зерттеңіз
қатарын
жинақтылыққа зерттеңіз
Жинақты
 қатарын
жинақтылыққа зерттеңіз
қатарын
жинақтылыққа зерттеңіз
жинақсыз
 қатарын
жинақтылыққа зерттеңіз
қатарын
жинақтылыққа зерттеңіз
жинақты
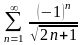 қатарын
жинақтылыққа зерттеңіз
қатарын
жинақтылыққа зерттеңіз
шартты жинақты
 қатарын
жинақтылыққа зерттеңіз
қатарын
жинақтылыққа зерттеңіз
жинақсыз
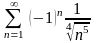 қатарын
жинақтылыққа зерттеңіз
қатарын
жинақтылыққа зерттеңіз
абсолютті жинақты
 қатарын
жинақтылыққа зерттеңіз
қатарын
жинақтылыққа зерттеңіз
абсолютті жинақты
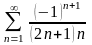 қатарын
жинақтылыққа зерттеңіз
қатарын
жинақтылыққа зерттеңіз
абсолютті жинақты
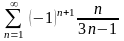 қатарын
жинақтылыққа зерттеңіз
қатарын
жинақтылыққа зерттеңіз
жинақсыз
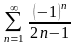 қатарын
жинақтылыққа зерттеңіз
қатарын
жинақтылыққа зерттеңіз
шартты жинақты
 қатарын
жинақтылыққа зерттеңіз
қатарын
жинақтылыққа зерттеңіз
абсолютті жинақты
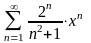 дәрежелік
қатарының жинақтылық радиусы тең:
дәрежелік
қатарының жинақтылық радиусы тең:

 дәрежелік
қатарының жинақтылық радиусы тең:
дәрежелік
қатарының жинақтылық радиусы тең:
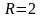
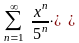 дәрежелік
қатарының жинақтылық радиусы тең:
дәрежелік
қатарының жинақтылық радиусы тең:
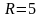
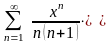 қатарының
жинақталу облысын табыңыз
қатарының
жинақталу облысын табыңыз
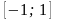
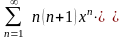 қатарының
жинақталу облысын табыңыз
қатарының
жинақталу облысын табыңыз
(-1, 1)
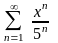 қатарының
жинақталу облысын табыңыз
қатарының
жинақталу облысын табыңыз
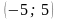
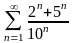 қатарының
қосындысын табыңыз
қатарының
қосындысын табыңыз
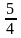
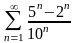 қатарының
қосындысын табыңыз
қатарының
қосындысын табыңыз
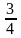
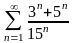 қатарының
қосындысын табыңыз
қатарының
қосындысын табыңыз
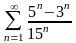 қатарының
қосындысын табыңыз
қатарының
қосындысын табыңыз
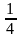
 қатарының
қосындысын табыңыз
қатарының
қосындысын табыңыз
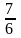
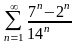 қатарының
қосындысын табыңыз
қатарының
қосындысын табыңыз
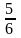
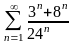 қатарының
қосындысын табыңыз
қатарының
қосындысын табыңыз
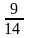
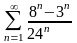 қатарының
қосындысын табыңыз
қатарының
қосындысын табыңыз
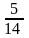
 қатарын
жинақтылыққа зерттеңіз
қатарын
жинақтылыққа зерттеңіз
Жинақты
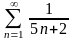 қатарын
жинақтылыққа зерттеңіз
қатарын
жинақтылыққа зерттеңіз
Жинақсыз
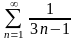 қатарын
жинақтылыққа зерттеңіз
қатарын
жинақтылыққа зерттеңіз
Жинақсыз
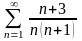 қатарын
жинақтылыққа зерттеңіз
қатарын
жинақтылыққа зерттеңіз
Жинақсыз
 қатарын
жинақтылыққа зерттеңіз
қатарын
жинақтылыққа зерттеңіз
жинақсыз
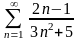 қатарын
жинақтылыққа зерттеңіз
қатарын
жинақтылыққа зерттеңіз
Жинақсыз
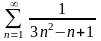 қатарын
жинақтылыққа зерттеңіз
қатарын
жинақтылыққа зерттеңіз
Жинақты
 қатарын
жинақтылыққа зерттеңіз
қатарын
жинақтылыққа зерттеңіз
Жинақсыз
у,
р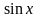
 ,Ln
, Z, n , €
,Ln
, Z, n , €
 параметрінің
қандай мәндерінде
параметрінің
қандай мәндерінде
 қатары жинақты?
қатары жинақты?
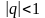
функциясының Маклорен қатарына жіктелуін көрсетіңіз

функциясының Маклорен қатарына жіктелуін көрсетіңіз

 санын
санын
 дәлдікке дейін есептеңіз
дәлдікке дейін есептеңіз
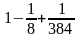
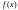 функциясының
функциясының
 нүктесінде Тейлор қатарына жіктелуін
көрсетіңіз
нүктесінде Тейлор қатарына жіктелуін
көрсетіңіз
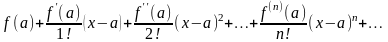
 функциясының
дәрежелік қатарға жіктелуін көрсетіңіз
функциясының
дәрежелік қатарға жіктелуін көрсетіңіз
 ,
,
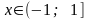
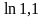 санын
дәлдікке дейін есептеңіз
санын
дәлдікке дейін есептеңіз
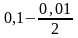
p
–
параметрінің қандай мәндерінде
 - Дирихле қатары жинақты болады?
- Дирихле қатары жинақты болады?

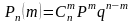 -
теңдікпен анықталатын үлестірімді
белгілеңдер
-
теңдікпен анықталатын үлестірімді
белгілеңдер
биномдық үлестірім
 функциясы
үшін Маклорен қатарының жалпы мүшесі
функциясы
үшін Маклорен қатарының жалпы мүшесі

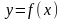 функциясы
үшін
функциясы
үшін
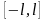 кесіндісіндегі Фурье қатарының
коэффициенттері
кесіндісіндегі Фурье қатарының
коэффициенттері
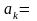
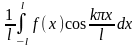
функциясы
үшін
 кесіндісіндегі Фурье қатарының
коэффициенттері
кесіндісіндегі Фурье қатарының
коэффициенттері


-ге
дейінгі дәлдікпен
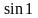 шамасын есептеу өрнегін көрсетіңіз
шамасын есептеу өрнегін көрсетіңіз

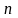 элементтен
жасалған алмастырулар саны
элементтен
жасалған алмастырулар саны
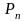 қай формуламен есептелінеді?
қай формуламен есептелінеді?

элементтен
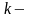 дан
жасалған теру
дан
жасалған теру
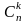 қалай есептелінеді?
қалай есептелінеді?

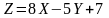 кездейсоқ
шаманың математикалық күтімін тап,
егер
кездейсоқ
шаманың математикалық күтімін тап,
егер
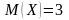 және
және
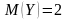 болса:
болса:

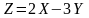 кездейсоқ
шаманың математикалық күтімін тап,
егер
кездейсоқ
шаманың математикалық күтімін тап,
егер
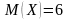 және
болса:
және
болса:
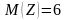
Сандар
|
-1 |
2 |
3 |
|
0,1 |
0,3 |
|
дискреттік шама: - тің үлестірім заңы болуы үшін тең:

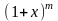 функциясының
Маклорен қатарына жіктелуін көрсетіңіз
(
функциясының
Маклорен қатарына жіктелуін көрсетіңіз
(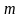 кез
келген тұрақты сан)
кез
келген тұрақты сан)
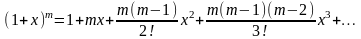 ,
,
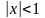
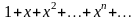 ,
,
қатарының қосындысын табу керек
,
,
қатарының қосындысын табу керек
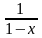
 ,
қатарының қосындысын табу керек
,
қатарының қосындысын табу керек

 қатардың
жалпы мүшесін табыңыз
қатардың
жалпы мүшесін табыңыз
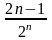
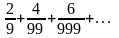 қатардың
жалпы мүшесін табыңыз
қатардың
жалпы мүшесін табыңыз

 қатарының
жинақтылыққа зертте
қатарының
жинақтылыққа зертте
Жинақты
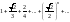 қатарын
жинақтылыққа зерттеңіз
қатарын
жинақтылыққа зерттеңіз
Жинақты
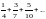 қатарының
жалпы мүшесін табыңыз
қатарының
жалпы мүшесін табыңыз
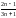
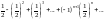 қатарының
қосындысын табыңыз
қатарының
қосындысын табыңыз
1/3
 қатарының
жалпы мүшесін табыңыз
қатарының
жалпы мүшесін табыңыз
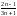
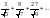 қатарының
жалпы мүшесін табыңыз
қатарының
жалпы мүшесін табыңыз
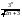
 қатарының
жалпы мүшесін табыңыз
қатарының
жалпы мүшесін табыңыз
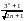
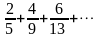 қатарының
жалпы мүшесін табыңыз
қатарының
жалпы мүшесін табыңыз

 қатарын
жинақтылыққа зерттеңіз
қатарын
жинақтылыққа зерттеңіз
жинақсыз
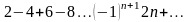 қатарын
жинақтылыққа зерттеңіз
қатарын
жинақтылыққа зерттеңіз
Жинақсыз
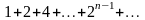 қатарын
жинақтылыққа зерттеңіз
қатарын
жинақтылыққа зерттеңіз
жинақсыз
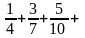 ...
қатарының жалпы мүшесін жазыңыз:
...
қатарының жалпы мүшесін жазыңыз:
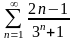
4 карточкалардың әр қайсысына Б, Е, Н, О әріптері жазылған. Осы карточкаларды араластырып, кездейсоқ бір қатарға (бірінен кейін бірін) орналастырғанда «небо» деген сөздің жазылу ықтималдығын тап
1/24
36 карталы колодадан кездейсоқ алынған карта «тұз» болу ықтималдығы неге тең?
1/9
7 адамнан құрамы 3 адамнан тұратын комиссияны қанша әдіспен құруға болады?
35
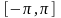
кесіндісіндегі жұп функциясы үшін Фурье қатары-

кесіндісіндегі тақ функциясы үшін Фурье қатары-
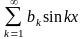
кесіндісіндегі жұп функциясы үшін Фурье қатарының коэффициенттері

кесіндісіндегі тақ функциясы үшін Фурье қатарының коэффициенттері

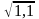 санын
дәлдікке дейін есептеңіз
санын
дәлдікке дейін есептеңіз

кесіндісіндегі жұп функциясы үшін Фурье қатары-
 интервалында
берілген
интервалында
берілген
 функциясын Фурье қатарына жіктеңіз
функциясын Фурье қатарына жіктеңіз
1
интервалында
берілген
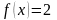 функциясын Фурье қатарына жіктеңіз
функциясын Фурье қатарына жіктеңіз
2
интервалында
берілген
 функциясын Фурье қатарына жіктеңіз
функциясын Фурье қатарына жіктеңіз
3
интервалында
берілген
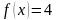 функциясын Фурье қатарына жіктеңіз
функциясын Фурье қатарына жіктеңіз
4
интервалында
берілген
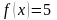 функциясын Фурье қатарына жіктеңіз
функциясын Фурье қатарына жіктеңіз
5
Ааааааа
**
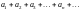 қатарының абсолютті жинақты болу
шартын көрсетіңіз
қатарының абсолютті жинақты болу
шартын көрсетіңіз
 қатар
жинақты
қатар
жинақты
**
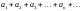 қатарының шартты жинақты болуының
анықтамасы :
қатарының шартты жинақты болуының
анықтамасы :
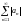 қатар
жинақсыз болып, ал
қатар жинақты болса
қатар
жинақсыз болып, ал
қатар жинақты болса
** дәрежелік қатардың жинақтылық радиусын
көрсетіңіз
дәрежелік қатардың жинақтылық радиусын
көрсетіңіз

**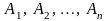 оқиғалары тәуелсіз болсын. Осы оқиғалардың
ең болмағанда біреуінің (А оқиғасы)
пайда болу ықтималдығы мына формуламен
анықталады:
оқиғалары тәуелсіз болсын. Осы оқиғалардың
ең болмағанда біреуінің (А оқиғасы)
пайда болу ықтималдығы мына формуламен
анықталады:
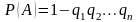
**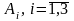 -
оқиғалар толық топты оқиғаларын құрады
және
-
оқиғалар толық топты оқиғаларын құрады
және
 .
Онда
.
Онда
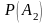 тең:
тең:
0,5
**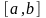 кесіндісінен мәндер қабылдайтын
үзіліссіз кездейсоқ шама
кесіндісінен мәндер қабылдайтын
үзіліссіз кездейсоқ шама тің
математикалық күтімі мына формула
арқылы табылады
тің
математикалық күтімі мына формула
арқылы табылады
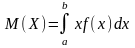
** Абонент телефон нөмірлерін тергенде соңғы екі цифрын ұмытып қалған, бірақ екі цифрдың әртірлі екендігі есінде. Абонент телефон соққанда цифрларды дұрыс теру ықтималдығын тап.
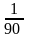
**
Ауыспа таңбалы
 қатарының жинақты болу шартын көрсетіңіз
қатарының жинақты болу шартын көрсетіңіз
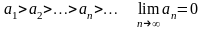
** Ақиқат оқиғаның ықтималдығы тең:
1
**Атқыштың нысанаға тигізу ықтималдығы 0,7 болса, онда екі рет атқанда ең болмағанда бір рет тигізу ықтималдығын табыңыз.
0,91
**Атқыштың нысанаға тигізу ықтималдығы 0,7-ге тең. Оның нысанаға атқан екі оғының екеуінің де нысанаға тию ықтималдығын тап
0,49
ӘӘӘӘӘӘӘ
**Әртүрлі үш (бірінші, екінші, үшінші) бәйгені қанша әдіспен 7 адамға беруге болады?
210
**Әрбір Ө, Н, Ж, Е, Д, У әріптері бөлек карталарға жазылған. Содан кейін карталар араластырылып, кез-келген ретпен бір қатарға орналастырылған. Сонда «ЖӨНДЕУ» сөзінің пайда болу ықтималдығы қандай?
A)
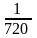
**Әрқайсысында бір әріп жазылған карталардан «САЛМАҚ» сөзі құрылған. Карталарды араластырып, содан кейін бір-бірлеп алған ретімен сөз құрастырылады Сонда «ЛАҚ» сөзінің пайда болу ықтималдығы қандай?
A)
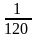
БББББББББ
***Бернулли
формуласын көрсет (мұндағы
 -
-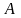 оқиғасының бір тәжірибеде орындалу,
ал
сол тәжірибеде орындалмау ықтималдықтары)
оқиғасының бір тәжірибеде орындалу,
ал
сол тәжірибеде орындалмау ықтималдықтары)

*** Бейес формуласын көрсет
![]()
Ггггггггггг
Гармоникалық қатарды көрсетіңіз

Ддддддддддд
***Даламбер
белгісі бойынша
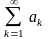
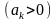 қатары жинақты, егер
қатары жинақты, егер


***Дисперсияны есептеу формуласын табыңыз
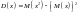
***Дискретті кездейсоқ шаманың математикалық күтімін көрсетіңіз
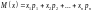
***Дискретті кездейсоқ шама Х-тің дисперсиясын табыңыз:
х i 1 2 5
р i 0,6 0,2 0,2
2
***Дәрежелік
қатардың
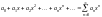 жинақтылық радиусын көрсетіңіз
жинақтылық радиусын көрсетіңіз

***Дәрежелік
қатардың
 жалпы мүшесінің коэффициенті тең:
жалпы мүшесінің коэффициенті тең:

***Дәрежелік
қатардың
 жалпы мүшесі келесі функция болады:
жалпы мүшесі келесі функция болады:

***Дәрежелік
қатардың
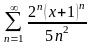 жалпы мүшесі келесі өрнек болады:
жалпы мүшесі келесі өрнек болады:

***Дәрежелік
қатардың
 жалпы мүшесінің коэффициенті тең:
жалпы мүшесінің коэффициенті тең:
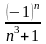
***Дәрежелік
қатардың
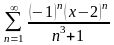 жалпы мүшесі келесі өрнек болады:
жалпы мүшесі келесі өрнек болады:
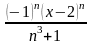
***Дәрежелік
қатардың
 жалпы мүшесі келесі өрнек болады:
жалпы мүшесі келесі өрнек болады:
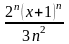
***Дәрежелік қатардың жалпы мүшесінің коэффициенті тең:
***Дүкенге кірген сатып алушы -ге тең ықтималдықпен зат сатып алады. Төрт адамның екеуі зат сатып алу ықтималдығын тап.

ЕЕЕЕЕЕЕЕЕЕЕ
*** функциясының Маклорен қатарына жіктелуін
көрсетіңіз
функциясының Маклорен қатарына жіктелуін
көрсетіңіз

Екі монетаны қатарынан лақтырғанда екеуінде де «герб» түсу ықтималдығы неге тең?
1/4
***Егер
сандық қатар
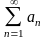 жинақты болса, онда
жинақты болса, онда
***Егер
және
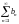 қатарларының
қатарларының
 мүшелері үшін
мүшелері үшін
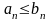 теңсіздіктер орындалса, онда :
теңсіздіктер орындалса, онда :
 қатарының
жинақтылығынан
қатарының
жинақтылығынан
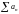 қатардың жинақтылығы шығады
қатардың жинақтылығы шығады
***Егер
,
жинақты, ал
 болса, онда
болса, онда
 қатары
қатары
жинақты
***Егер
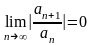 болса, онда
болса, онда
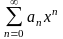 дәрежелік қатарының жинақтылық радиусы
неге тең?
дәрежелік қатарының жинақтылық радиусы
неге тең?
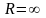
***Егер
 ,
,
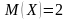 болса, онда дискретті кездейсоқ шама
Х-тің дисперсиясы
болса, онда дискретті кездейсоқ шама
Х-тің дисперсиясы
 -ті
табыңыз.
-ті
табыңыз.
21
***Егер
 дәрежелік қатары нөлге тең емес
дәрежелік қатары нөлге тең емес
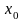 нүктесінде жинақты болса, онда :
нүктесінде жинақты болса, онда :
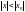 теңсіздігін
қанағаттандыратын барлық
теңсіздігін
қанағаттандыратын барлық
 тер
үшін қатар абсолютті жинақты болады
тер
үшін қатар абсолютті жинақты болады
***Егер
дәрежелік
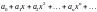 - қатары
нүктесінде жинақсыз болса, онда ол :
- қатары
нүктесінде жинақсыз болса, онда ол :
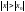 теңсіздігін
қанағаттандыратын барлық
тер
үшін жинақсыз болады
теңсіздігін
қанағаттандыратын барлық
тер
үшін жинақсыз болады
***Егер
 қатары жинақты болса, онда
қатары жинақты болса, онда
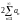 қатары туралы не айтуға болады?
қатары туралы не айтуға болады?
Жинақты
***Егер
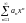 қатары
қатары
 нүктесінде жинақты болса, онда қатар
:
нүктесінде жинақты болса, онда қатар
:
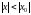 болғанда
әрбір
болғанда
әрбір
 нүктесінде абсолютті жинақты
нүктесінде абсолютті жинақты
***Екі үйлесімсіз А және В оқиғаларының қосындысының ықтималдығы тең:
P(A+B)=P(A)+P(B)
***Екі тәуелсіз оқиғалардың көбейтіндісінің ықтималдығы тең:
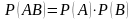
***Екі тәуелді оқиғалардың көбейтіндісінің ықтималдығы тең:

***Екі үйлесімді оқиғалардың қосындысының ықтималдығы тең: