5. Регрессионный анализ

5.1 Модель регрессии

Рассмотрим задачу: случайная величина является некоторой функцией от случайных величин . Произведены наблюдения

,	,	…	,
,	,	…	,
…	…	…	…
,	,	…	,

над случайными величинами и в результате по каждому наблюдению получена реакция случайной величины в виде . Требуется найти вид зависимости

. (5.1)

Такая зависимость называется регрессией по (на) , т.е. условное математическое ожидание при известных значениях . В этом случае величины называются независимыми переменными [9] (объясняющими переменными [7] и т. д.), величины называются зависимыми переменными. Возможна другая постановка задачи, когда величины принимаются за независимые переменные, а величины - за зависимые переменные. В этом случае необходимо определить зависимость

, (5.2)

которая называется регрессией по (на) . Выбор типа переменной зависит от решаемой задачи и здравого смысла.

Если бы не было случайных ошибок в результате эксперимента, зависимость можно было бы построить точно. Но с учетом ошибки имеем

, (5.3)

где U - случайная величина, обусловленная или неправильным выбором функции , или ошибкой записи, или другими случайными явлениями. В дальнейшем будем эти зависимости описывать через их реализации

, (5.4)

где - регистрируемая величина,

- ожидаемая величина (функциональная зависимость).

Обычно ,

Наиболее простая зависимость - линейная функция относительно параметра :

. (5.5)

Линейность понимается в том смысле, что коэффициенты входят в выражение для функции в первой степени. Функции считаются известными и выбираются самим экспериментатором на основе опыта и полученных данных.

Простейшая линейная модель: .

В этом случае уравнение регрессии примет вид

.

Более сложная модель: . В этом случае предполагается, что аргументы отражают различные величины. Модель регрессии будет иметь вид

. (5.6)

Этот вид регрессионной зависимости часто встречается в экономических задачах, когда переменные являются различными экономическими показателями предприятия. В результате анализа работы предприятия получают таблицу значений

,	,	…	,
,	,	…	,
…	…	…	…
,	,	…	,

используемые в дальнейшем для определения коэффициентов регрессии .

Приведём другую модель регрессии, линейную относительно параметров , - степенную регрессию:

. (5.7)

На основе экспериментальных данных и необходимо определить величины . В качестве критерия выбора величины во всех приведенных моделях берётся критерий минимума среднеквадратической ошибки (критерий минимума СКО):

. (5.8)

Наблюдения и зависимые переменные удобно представить в виде таблицы

1	y1		...
2	y2		...
3	y3		...
n	yn		...

За значения принимают те значения , которые минимизируют форму (5.8). Произведем дифференцирование по , выражения (5.8) и приравняем его нулю. В результате имеем систему линейных уравнений относительно параметров :

…………………………………………………………………

В свернутой форме эта система уравнений имеет вид

. (5.9)

Систему уравнений (5.9) в статистике называют системой нормальных уравнений и её можно представить в матричной форме.

Обозначим

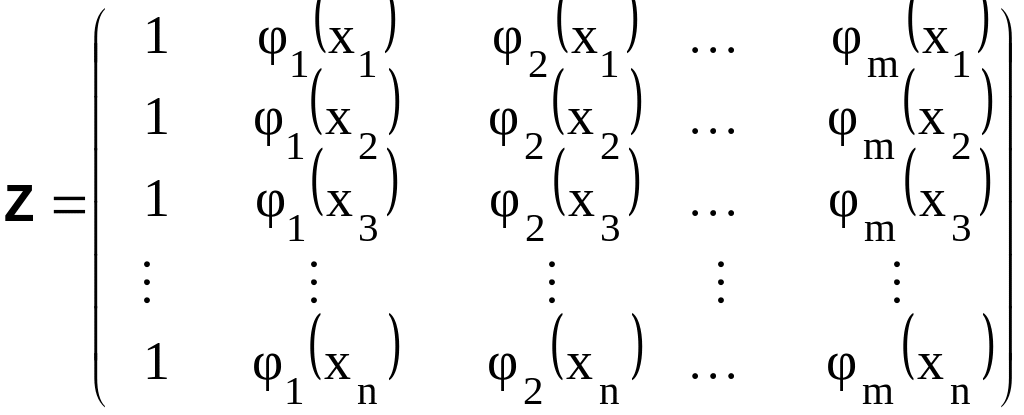. (5.10)

Тогда система (5.9) имеет вид

, (5.11)

.

Решением этой системы будет вектор оценки параметров

. (5.12)

В силу того, что наблюдения носят случайный характер, составляющие вектора будут случайными величинами с математическим ожиданием и корреляционной матрицей .