3.3 Исключение грубых погрешностей
Рассмотрим задачу
исключения грубых погрешностей из ряда
измерений
[4, стр. 58]. Пусть
-взаимно
независимые нормально распределенные
случайные величины с
,
.
Проверяется гипотеза
о том, что
.
Альтернативная гипотеза:
и
.
Величина d
может быть и положительной и отрицательной,
если d
> 0, то проверяется альтернативная
гипотеза
,
а если d
< 0, то проверяется альтернативная
гипотеза
.
Причем номер испытания
,
на котором допущена ошибка d
и ее величина неизвестны.
Перепишем
последовательность
в виде вариационного ряда
.
Тогда
.
В зависимости от того известны или нет
значения параметров
,
можно получить 4 задачи проверки гипотезы
.
Рассмотрим только одну задачу с
неизвестными параметрами
,
т.е. вместо
используем их оценки
по формулам
,
.
Оценки
и
являются несмещёнными, состоятельными
и эффективными.
Несмещенная оценка
дисперсии
- имеет
степень свободы. Рассмотрим статистики
,
,
,
в которых, в принципе, может применяться как смещенная, так и несмещенная дисперсия; поэтому индекс у среднеквадратического отклонения опущен.
Получим вероятностные
зависимости между статистиками
,
,
.
Нормированное нормальное распределение
симметрично относительно оси ординат.
Поэтому все статистики
и
с соответствующими аргументами
распределены одинаково (например,
и
) и
-квантили
распределения
лишь знаком отличаются от
-квантилей
распределения статистики
:
.
(3.5)
Из этого равенства
следует, что для вычисления
достаточно знать
.
Равенство (3.5) можно представит как
.
Из этого соотношения получим
(3.6)
Событие
может быть представлено как сумма двух
несовместных событий:
и
.
Тогда имеем
(3.7)
Подставляя (3.6) в (3.7), получим
Откуда
.
Положим
- граница критического множества, и
определяет критическое множество, т.е.
такое множество, что при попадании
статистики
в это множество гипотеза
отвергается. Из предыдущего ясно, что
вероятность отвергнуть гипотезу
по статистике
при верности гипотезы
не превышает
,
где
является уровнем значимости для проверки
гипотезы
по статистике
.
Пусть
- уровень значимости при проверке
гипотезы
.
Если бы была
составлена таблица для
,
то ею можно было бы воспользоваться для
проверки гипотезы
:
.
Однако такой таблицы нет.
В [4, стр. 59] со ссылкой на [6] приводится неравенство
,
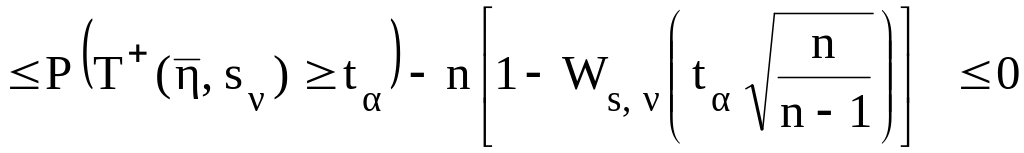(3.8)
где
- функция распределения Стьюдента с
степенями свободы. Ввиду того, что
математическое ожидание
и дисперсия
- неизвестны, и они оцениваются по
выборке, то число степеней свободы
распределения Стьюдента
.
Перепишем неравенство (3.8) в виде
(3.9)
Это неравенство позволяет вычислить приближённо квантиль распределения статистики по заданному уровню значимости α.
Если применяется
смещенная оценка
,
то приближенно можно оценить квантиль
распределения статистики
по заданному уровню значимости α при
помощи неравенства [4]
(3.10)
где
- функции распределения Стьюдента с
степенями свободы.
Пример 3.2 Определим
критическое значение при отбраковке
величины
по заданному числу испытаний
и уровню значимости
,
если оценки
и
- несмещённые.
Для решения задачи
используем статистику
и неравенство (3.9) для оценки вероятности
по данному уровню значимости. При
вычислении выражений, входящих в
неравенства (3.8) использовался пакет
Mathematica.
Программа вычислений приведена в
Приложении.
Левая часть
неравенства (3.9) дает значение
=
t0=
=3.1539768 для
уровня значимости
0.049999995.
Определим
.
Правая часть
неравенства (3.9) дает значение
=
t0= =3.1692727 для
уровня значимости
.
0.049999997.
Определим
.
Существует некоторый
произвол в выборе критического значения
или
,
так как они оба обеспечивают один и тот
же уровень значимости. Выберем
.
Вывод. Если
статистика
>
,
гипотеза
отвергается с уровнем значимости, не
превышающей
0.04999999.