1.2 Распределение Фишера

Рассмотрим две случайные величины и , имеющих -распределение с n и m степенями свободы, соответственно, где и взаимно независимые нормально распределенные случайные величины с , , , . Их отношение

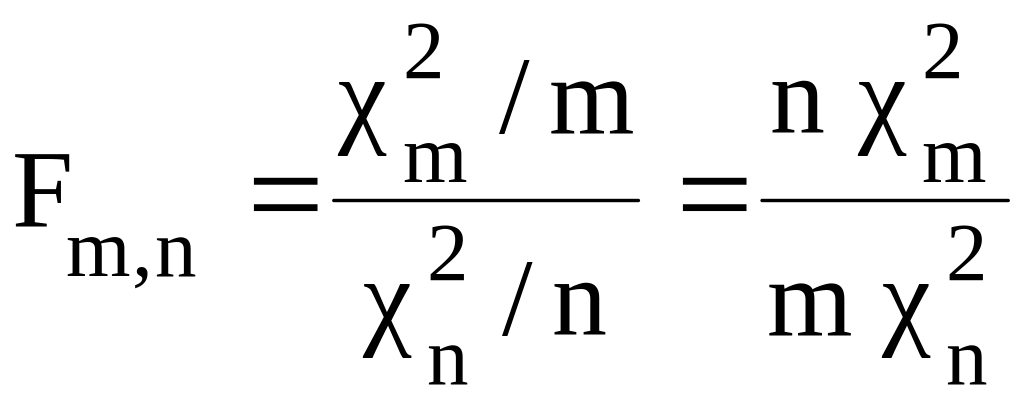
называется -отношением с и степенями свободы и имеет плотность распределения вероятностей вида [4, стр.32]

, (1.14)

называемая плотностью вероятности -распределения или распределением плотности вероятности Фишера.

Для распределения Фишера составлены таблицы как функции числа степеней свободы и величины , определяемой выражением (1.15), [4, Таблица 3.5, стр. 200],

= . (1.15)

Величину называют Q-процентным критическим значением или Q% пределом.

-распределение часто применяется для проверки гипотез.

Если дисперсии и неизвестны, то для проверки гипотезы : ,( - известная величина), составляется отношение

, (1.16)

где , - несмещённые оценки дисперсий и , распределенных по закону с и степенями свободы соответственно,

, - оценки математических ожиданий и

Отношение (1.16) имеет F-распределение с и степенями свободы,[15, стр. 128].

В качестве альтернативной гипотезы примем : .

Критическая область при проверке гипотезы будет определяться неравенством

.

Пример. Положим = 10, , k=2, требуемый уровень значимости . Определить критическую область. По заданным m, n и Q определяем число степеней свободы и допустимый процент ошибки отклонения гипотезы в то время, как она верна.

. Из таблиц [4, стр. 208] находим

= 3.6767. Критической областью будет множество (7.3534,  ). Если отношение 7.3534, гипотеза отвергается.

2. Проверка гипотез

Проверка гипотез наиболее часто встречающаяся задача при обработке экспериментальных данных. Предполагается, что имеются результаты наблюдений из выборочного пространства над источником информации , которым соответствует некоторая функция распределения .

Тип источника информации может быть различным:

- источник с дискретными состояниями ,

- источник с непрерывными состояниями , где - границы непрерывного множества.

Априорную информацию о типе источника считаем известной, но параметры, описывающие состояние источника – неизвестны. Эти параметры влияют на закон распределения выборочных значений . Поэтому будем считать, что вид распределения и его параметры неизвестны наблюдателю. В общем случае может быть выдвинута гипотеза о виде распределения или о его параметрах, (математическое ожидание, дисперсия, корреляционный момент, интервал стационарности и т.д.). Гипотезы о величине параметров будем называть параметрическими гипотезами. В то же время необходимо проверять гипотезы о типе распределения или о том, что две выборки и относятся к одному и тому же распределению. Такие гипотезы будем называть непараметрическими гипотезами.

Рассмотрим двухальтернативные гипотезы и о состоянии источника: : , : , таких, что . Возможно два решения:

- не отклонять гипотезу ,

- отклонить гипотезу .

Разделим выборочное пространство на две части и таких, что Ø.

Выдвинем гипотезу о том, что выборка принадлежит выборочному пространству , описываемому функцией распределения . В зависимости от проверяемой гипотезы (мат. ожидание и т.д.) рассматриваются различные свойства выборочного пространства .

Гипотеза не отвергается, если выборка принадлежит пространству и отвергается, если выборка принадлежит пространству , т.е. принимается альтернативная гипотеза .

Подмножество выборок, составляющих выборочное подпространство , называется критической областью критерия, а условная вероятность

(2.1)

называется уровнем значимости или уровнем критерия.

Уровень значимости предполагает отклонение гипотезы , в то время как она верна, в случаев статистической проверки гипотезы .

Условная вероятность того, что выборка принадлежит подпространству при состоянии источника :

, (2.2)

называется мощностью критерия.

Мощность критерия предполагает принятие гипотезы , в то время как источник находится в состоянии , в случаев статистической проверки гипотезы .

Положим, происходит проверка гипотезы о параметрах распределения и пусть распределение содержит M параметров. Если проверяется гипотеза о K параметрах распределения и K=M, то гипотеза называется простой, если K<M , гипотеза называется сложной.

Например, нормальный закон описывается двумя параметрами (математическим ожиданием и дисперсией ). Если проверяется гипотеза : и , то гипотеза - простая. Если проверяется гипотеза : , и , то гипотеза - сложная.

Критерий проверки гипотезы : против сложной альтернативной гипотезы : , называется несмещенным, если мощность критерия удовлетворяет условию [17, стр. 174]

.

В этом случае область называется несмещенной критической областью.

Критерий проверки простой гипотезы против альтернативной гипотезы о состоянии источника называется состоятельным, если

.

Эти соотношения говорят о том, что при возрастании числа наблюдений разумно отклонить ложную гипотезу.

Положим, происходит проверка простой гипотезы против сложной гипотезы . Согласно гипотезе параметр распределения может принимать значения из некоторого множества. Для каждого значения параметра согласно гипотезе (т.е. для заданного значения ) можно найти критические множества . Если существует такое критическое множество среди всех возможных, что мощность критерия будет наибольшей, то такое множество называется равномерно наиболее мощным, а критерий, по которому происходит проверка, называется равномерно наиболее мощным критерием (РНМ критерий).

Например, теорема Неймана-Пирсона позволяет найти РНМ множество и построить РНМ критерий.

РНМ критерий существует для проверки простой гипотезы ( ) против сложной альтернативной гипотезы ( ). Но, если альтернативной гипотезой является , то РНМ критерия не существует, т.к. должны существовать два подмножества и , соответствующие и , для которых имеется одна и та же мощность . Это может быть только тогда, когда (если используется критерий отношения правдоподобия, [3, стр 235]):

,

где - функция правдоподобия.

Если измерения независимы, .

Значимость критерия равна ,

мощность критерия равна .

- граница критической области с уровнем значимости .

Положим, выдвигается гипотеза или о типе распределения измеряемого параметра, или о величине измеряемого параметра. Мерой соответствия выдвигаемой гипотезы реальному состоянию исследуемой проблемы является вероятность отклонения статистической гипотезы в то время как она верна.

Пусть произведена выборка из генеральной совокупности , характеризуемой параметром . Экспериментатору неизвестно значение параметра . Для того, чтобы выяснить значение параметра вычисляется оценка , как некоторая функция от выборки.

Рассмотрим задачу проверки гипотезы о том, что оценка принадлежит генеральной совокупности . Альтернативной гипотезой будет утверждение: оценка не принадлежит генеральной совокупности. Гипотеза отвергается, если абсолютное уклонение оценки от истинного значения превышает некоторую величину . Вероятностной мерой расхождения оценки от параметра является условная вероятность отклонения от при верности гипотезы :

, (2.3)

где - уровень значимости ошибки при принятии решения,

- критическое значение - постоянная, зависящая от уровня значимости и распределения оценки .

Уровень значимости показывает степень доверия к принятому решению. Если гипотеза верна, то согласно (2.3) возможно её отклонить, (выполнится неравенство ), в случаях проверки гипотезы в серии из 100 проверок гипотезы . При верности гипотезы в большой серии испытаний выполнение неравенства невозможно объяснить только лишь случайностью, т.к. вероятность довольно малая величина. Все точки, удовлетворяющие неравенству , образуют критическое множество.

Выражение (2.3) можно представит как

+

или

, (2.4)

где - является квантилем распределения вероятности :

(2.5)

На рисунке 2.1 затененные области соответствуют вероятности ошибки, равной , а области значений статистики , являются критическими областями.

Ввиду того, что имеются две критические области и , подобную процедуру проверки гипотезы против альтернативной гипотезы называют двусторонней, а гипотезу называют двусторонней гипотезой [7].

В то же время, если выполняется неравенство при верности гипотезы , гипотеза принимается с вероятностью

, (2.6)

где мощность критерия.

На практике встречаются случаи, когда проверяется гипотеза : или , или . Эта процедура проверки гипотезы называется односторонней, а сама гипотеза - односторонней гипотезой. Критическая область будет состоять из множества точек при проверке гипотезы : , или множества при проверке гипотезы: . На рисунке 2.2 приведен пример, иллюстрирующий критическую область и вероятность ошибки при проверке гипотезы : .

П ример проверки сложных гипотез. Пусть наблюдаемая величина подчиняется нормальному закону:

.

Проверяются гипотезы и :

: , - неизвестно,

: , - неизвестно.

Произведем оценки математического ожидания и дисперсии

, . (2.7)

Необходимо построить критическую область по заданному . Построим функции правдоподобия при верности гипотез и .

Если неизвестны значения параметров распределения, то в функции правдоподобия подставляются те значения параметров, которые обеспечивают наибольшие значения функций правдоподобия.

Используем это утверждение для построения отношения правдоподобия. Введём и вычислим функцию правдоподобия при истинности гипотезы :

: .

При верности гипотезы , ( ), оценкой дисперсии служит величина

.

Подставим в выражение , и учитывая, что

, получим

.

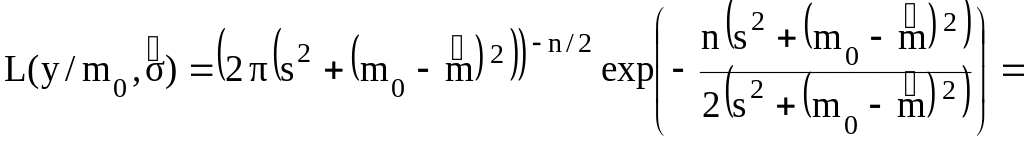
Вычислим функцию правдоподобия при истинности гипотезы . Ввиду того, что проверяется гипотеза , ( ), при альтернативной гипотезе , ( ), то в качестве произвольного для альтернативной гипотезы в качестве математического ожидания можно взять оценку .

: .

Тогда отношение правдоподобия примет вид

. (2.8)

Рассмотрим случайную величину

. (2.9)

Числитель этого выражения распределен по нормальному закону с математическим ожиданием, равным нулю, и дисперсией, равной 1.

Рассмотрим знаменатель выражения (2.9). Подставим вместо его значение . Величина распределена как . Пользуясь определением случайной величины из таблицы 1.1, законом распределения Стьюдента (1.13) и учитывая линейную связь , определим, что случайная величина распределена по закону Стьюдента с степенью свободы:

. (2.10)

Используя (2.8) и(2.9), запишем отношение правдоподобия в виде

(2.11)

и критическую область определим как

.

Распределение Стьюдента симметрично и для этого распределения существуют таблицы. Математическое ожидание и дисперсия величины равны соответственно , т.е. не зависят от параметров нормального распределения. Преобразуя выражение (2.12), получим

. (2.13)

Г рафик функции изображен на рисунке 2.3. Области и , (выделены жирными линиями), удовлетворяющие неравенству (2.13), образуют критические области, где и - квантили распределения Стьюдента с степенью свободы.

Для уровня значимости значение можно найти из решения уравнения

,

где - плотность распределения Стьюдента с степенью свободы. Ввиду симметричности плотности распределения Стьюдента имеем . Процедура проверки гипотезы сводится к проверке неравенства

.

При выполнении этого неравенства гипотеза не отвергается. В противном случае гипотеза отвергается. Ошибка отвергнуть гипотезу в то время как она верна, возможна в случаях из 100 испытаний.

Значение порога определяется как .

Критерий отношения правдоподобия применяется тогда, когда нет дополнительной априорной информации о состоянии источника. Но нельзя забывать, что этот критерий может привести к ошибочным выводам, что показано в следующем примере.

Пример,[3, стр. 330]. Случайная величина принимает значения с вероятностями , , указанными в таблице 2.1.

таких, что .

- известная константа, и - должны удовлетворять условиям:

, . (2.14)

Таблица 2.1

	-2	-1	0	1	2

Производится одно единственное наблюдение. Необходимо проверить гипотезу . Альтернативная гипотеза параметры и принимают все возможные значения, удовлетворяющие условию (2.14). В данном случае производится проверка простой гипотезы против сложной гипотезы .

Вычислим функции правдоподобия и , построим отношение правдоподобия и определим критическое множество. Если неизвестны значения параметров при верности той или иной гипотезы, то вместо и в функцию правдоподобия подставим те значения и , которые максимизируют функцию правдоподобия. Расчет функций правдоподобия.

1. =-2, ,

,

.

2. =-1, ,

,

,

3. =0,

,

.

4. =1, ,

,

.

5. =2, ,

,

.

Таким образом, получаем отношение правдоподобия

(2.15)

В качестве критерия принятия гипотезы примем выполнение условия:

гипотеза не отклоняется для тех выборочных значений , для которых отношение правдоподобия принимает наибольшие значения при .

Как видно, отношение правдоподобия зависит от и наибольшие значения принимает, при , (т.е. при ). Поэтому, если (-1, 0, +1), гипотеза не отвергается. Тогда критическим множеством будут точки (-2, +2).то есть если в результате эксперимента появятся значения , равные -2 или 2, гипотеза должна быть отвергнута.

Рассмотрим характеристики критерия отношения правдоподобия.

1. Мощность критерия:

,

но значение находится в интервале и при мощность критерия равна <0.5.

2. Значимость критерия, [3, стр. 232].

.

3. Смещение критерия отношения правдоподобия.

Гипотеза - сложная гипотеза. Согласно определению несмещенности критерия должно выполняться условие

, или ,

но по условию задачи . Получается, что вероятность правильного принятия гипотезы меньше 0.5, что является не приемлемым.

Вывод.

1. Критерий отношения правдоподобия - смещенный критерий, т.к. мощность критерия зависит от параметра и не превышает 0.5. Пользы от такого критерия нет.

2. Если , то .

Причиной смещения критерия является неправильный выбор критерия проверки гипотезы .

Выберем другой критерий: гипотеза отвергается, если , т.е. критическим множеством является точка и рассмотрим свойства такого критерия.

1. Мощность критерия. .

2. Значимость критерия: .

3. Проверка на смещение критерия:

должно выполняться условие . Подставим соответствующие вероятности в это неравенство

, ,

т.е. должно выполняться неравенство , что действительно выполняется при условии . Следовательно, принятый критерий – несмещенный критерий.

Вывод. К применению критерия отношения правдоподобия надо

подходить осторожно и необходимо проверять свойства критерия.