В результате эксперимента исследователь получает последовательность данных, по которым он должен сделать выводы об изучаемом явлении. Между полученными экспериментальными результатами и выводами существует раздел обработки полученных данных. В зависимости от выбранных методов обработки данных, от погрешностей, зависящих от метода обработки, можно придти к результатам или подтверждающим или опровергающим исследуемое явление. Поэтому правильность выбора методов обработки данных обеспечивает надёжность выводов.

Одним из первых шагов является отбраковка грубых ошибок. Грубые ошибки могут быть исключены из ряда наблюдений по субъективным причинам или путем статистической обработки данных. Статистические методы включают в себя методы, основанные на математической статистике, и на методах, использующие физические свойства полученных данных.

Часто бывает, неизвестны плотность распределения вероятности помех и тип помех, искажающие данные. В этом случае для некоторых задач обработки данных применяются методы непараметрической статистики.

Для построения функциональной зависимости по экспериментальным данным применяется регрессионный анализ, позволяющий не только найти коэффициенты регрессии, но и оценить погрешности, исследуемых параметров регрессии.

В методическом пособии приведены распределения вероятности некоторых случайных величин, используемых в дальнейшем. Кратко изложена теория обработки данных в применении к выше перечисленным задачам. Особое внимание уделяется примерам, показывающим неприменимость выбранного метода обработки данных с точки зрения математической статистики.

В приложении приведены программы моделирования процедуры обработки данных. Программы написаны с использованием пакета Mathematica.

Работа выполнена при поддержке гранта РФФИ № 04-05-65069.

1. Распределения, связанные с суммой случайных величин

1.1 Распределение Стьюдента

Методы обработки статистической информации связаны со знанием априорной информации об исследуемом явлении. Наиболее полная информация содержится в законе распределения вероятности измеряемой величины с известными характеристиками.

Например, биномиальный закон распределения характеризуется вероятностью реализации «1» или «0»: ;

нормальный закон зависит от двух параметров – математического ожидания и дисперсии .

Однако на практике, даже если известен закон распределения вероятности измеряемого параметра, часто неизвестны параметры закона распределения, такие как , , из выше приведенных примеров. Поэтому при решении статистических задач вместо теоретических величин используют статистические оценки , , . Использование статистических оценок приводит к некоторым погрешностям.

В свою очередь сами оценки, будучи результатом обработки экспериментальных данных, являются случайными величинами и обладают некоторым законом распределения вероятности. Эти законы распределения выводятся на основе априорно известных законов распределения измеряемого параметра. Желательно, чтобы эти законы распределения не зависели от оцениваемого параметра.

Положим, производится выборка объёма n (т.е. проводится эксперимент) и результаты эксперимента равны . В дальнейшем для построения правил исключения грубых ошибок понадобится закон распределения вероятности суммы квадратов независимых случайных величин :

. (1.1)

Если случайная величина имеет плотность вероятности, равную , то плотность распределения вероятности величины равна

, . (1.2)

Если случайная величина распределена по нормальному закону с математическим ожиданием и дисперсией, равными соответственно нулю и 1, из формулы (1.2) получим

, . (1.3)

Характеристическая функция сл. в. вычисляется как

. (1.4)

Пользуясь свойством характеристической функции, получим характеристическую функцию сл. в.

. (1.5)

И спользуя обратное преобразование, из (1.5) определим плотность распределения вероятности сл. в. [1, стр. 259]

, (1. 6)

которое называется плотностью -распределения с числом степеней свободы, равным . Число степеней свободы обусловлено независимостью выборочных значений .

Математическое ожидание и дисперсия сл. в. зависят от числа степеней свободы:

Вид ^-распределения зависит от числа степеней свободы. С увеличением числа степеней свободы ^-распределение стремится к нормальному распределению , что показано на рисунке 1.1.

Для решения некоторых задач в дальнейшем понадобятся плотность распределения оценки дисперсии

и

случайной величины , распределенной N(x, m, ).

Представим оценку в виде . В свою очередь это выражение можно записать как

или .

Случайные величины и имеют плотности распределения вероятности . Как известно, характеристическая функция суммы квадратов независимых нормально распределенных случайных величин имеет вид (1.5).

Случайные величины и независимы. Поэтому характеристическая функция суммы равна произведению характеристических функций соответствующих величин. Используя это, запишем

.

Из последнего выражения определим характеристическую функцию

.

Обратное преобразование характеристической функции позволяет вычислить плотность распределения величины , равную ^-распределению с степенью свободы:

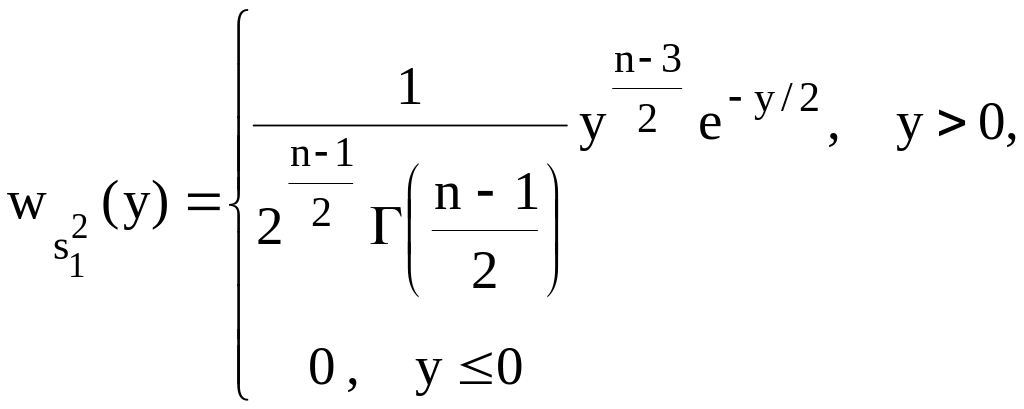(1.7)

Уменьшение степени свободы ^-распределения на 1 связано с тем, что существует линейная связь .

Оценка является линейным преобразованием величины , ( ). Поэтому плотность вероятности оценки будет иметь также степень свободы и вид

=

(1.8)

Рассмотрим следующие примеры. Пусть задана случайная величина , плотность распределения вероятности которой равна . Производится линейное преобразование

. (1.9)

Плотность распределения вероятности случайной величины равна

. (1.10) В частности, если величина распределена по нормальному закону и константы и равны и , соответственно, плотность распределения величины имеет вид

.

Используем линейное преобразование (1.9) и формулу (1.10), чтобы получить плотность распределения случайных величин

, ,

, ,

где случайные величины взаимно независимы и распределены по нормальному закону с и .

Плотности распределений перечисленных случайных величин приведены в таблице 1.1 [1]:

Таблица 1.1

Случайная величина может быть представлена как

,

где распределена по нормальному закону с и .

Рассмотрим величину

, (1.11)

где случайные величины и взаимно независимы и распределены по нормальному закону с математически ожиданиями и дисперсиями .

В силу независимости и случайные величины и будут также независимы. Совместная плотность распределения величин и равна произведению плотностей распределений

,

где .

Ф ункция распределения частного запишется как [1]

.

Область интегрирования показана на рисунке 1.2. В результате получим функцию распределения частного в виде

. (1.12)

Дифференцируя выражение (1.12) по , получим плотность распределения вероятности частного

.

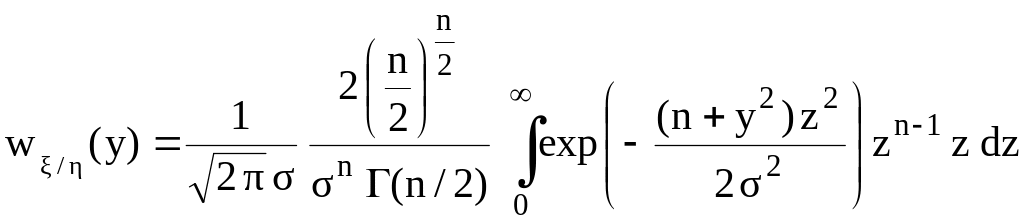Чтобы вычислить интеграл, произведем подстановку

и, учитывая, что , получим плотность распределения вероятности случайной величины

. (1.13)

П лотность распределения называется распределением Стьюдента или t- распределением с числом степеней свободы, равным n.

Как видно, плотность t-распределения не зависит от дисперсии . Математическое ожидание и дисперсия t-распределения равны, соответственно, нулю и . Графики функций для и представлены на рисунке 1.3.