3.2 Учебно-методические материалы лекционного курса Конспект лекций Тема: Группировка статистических данных, статистическое изучение взаимосвязи явлений.

Построение группировки

Прежде всего, при изучении данной темы необходимо уяснить, что группировка - важнейший метод статистического исследования. С ее помощью решают задачи: выделение социально-экономических типов, изучение состава совокупности и выявление зависимости результативного признака от изменения факторного признака. В соответствии с задачами исследования различают следующие виды группировок: типологические, структурные и аналитические.

Примером типологической группировки можно назвать группировку жилого фонда по формам собственности, выделяющую муниципальный, частный и ведомственный жилые фонды. К структурным относятся группировки населения по полу, возрасту, национальности и др. Для них характерны показатели: число единиц в группе, удельный вес группы в общей численности единиц или в общем объеме изучаемого признака. Для исследования взаимосвязи прибегают к аналитической группировке. При этом изучаемую совокупность расчленяют по факторному признаку и по каждой группе исчисляют среднее значение результативного признака, вариация которого от группы к группе покажет наличие или отсутствие зависимости.

Чтобы получить типологическую, структурную или аналитическую группировку из первичных данных, надо выполнить следующие операции:

1. Отобрать группировочный признак. При этом выполняют важнейшее требование теории группировок - глубокий теоретический анализ изучаемой совокупности, опирающийся на знание экономических законов развития общества, с целью выделения факторных признаков (влияющих на другие) и результативных (зависящих от изменения факторных). Из множества факторных признаков отбирают основные. По одному или нескольким из них осуществляют группировку. Признаки могут быть атрибутивными и количественными. Атрибутивные признаки принимают значения, выраженные словами. Количественные признаки бывают дискретные (принимающие целые числовые значения) и непрерывные (принимающие любые значения, даже дробные, располагающиеся в виде интервала.).

2. Определить число групп. Приступая к этому этапу группировки, следует обратить внимание на то, что выбор некоторых атрибутивных признаков в качестве группировочных предопределяет число групп. Например, группировка населения по полу приводит к образованию всего лишь двух групп: мужчины и женщины. Иногда количество групп заранее определяется условиями исследования.

3. Определить размер интервала. Если в основание группировки положен дискретный признак, имеющий множество записей, или непрерывный количественный, то число групп определяют одновременно с размером интервала. Когда совокупность единиц более или менее однородна, прибегают к равным интервалам, размер которых устанавливают приближенно по формуле Стержесса:

где i - размер интервала;

х_max, x_min - максимальное и минимальное значение группировочного признака в совокупности;

N - число единиц в совокупности;

1+3,322 lg N - приближенно показывает необходимое число групп (n).

Если число групп (n) задано, то формула для расчета интервала:

где п – число групп.

4. Определить границы каждой группы. Большое значение имеет четкое обозначение границ интервалов. Границы интервалов обозначаются обычно указанием значения признака от и до. Например, группы семей по их численному составу можно отграничить так: от 2 до 3 человек, от 4 до5 и т.д.

В первой группе значение 2 является нижней границей интервала, а 3 - верхней. Верхняя граница первого интервала не совпадает с нижней границей следующего интервала. При подобном обозначении границы между группами четко очерчены.

Часто границы интервалов обозначаются так, что верхняя граница численно совпадает с нижней границей следующего интервала. Например: в группировке работников по размеру заработной платы с интервалами:

до 120 000,

120 000-160 000,

160 000-200 000,

200 000- 240 000

В данном случае наблюдается совпадение границ. Отграничение групп здесь проведено с помощью первого открытого (не имеющего одной границы) интервала. Судя по нему, работников с заработной платой 120 000 рублей нужно отнести во вторую группу, с оплатой 160 000 рублей - в третью и т.д.

Если открытых интервалов нет, для отграничения границ групп необходимо каждую нижнюю границу группы (или каждую верхнюю границу) увеличить (уменьшить) на одну разрядную единицу.

5. Зашифровать данные, построить вспомогательную (разработочную) таблицу и разнести в нее данные по группам.

6. По каждой группе в разработочной таблице определить итоговые показатели.

7. С учетом требуемых данных построить итоговую таблицу.

8. Итоговые данные по группам вынести в сводную таблицу и дополнительно просчитать средние показатели по группам. Сводная таблица, полученная в результате и будет представлять собой группировку.

9. Сделать выводы по полученным данным.

Таким образом проводится группировка статистических данных.

Построение модели связи между признаками. Метод корреляционно-регрессионного анализа устанавливает наличие, форму и вид взаимосвязи результативных и факторных признаков, определяя их уровень (тесноту) связи и оценивая использование факторов единицами наблюдения (предприятий).

Нахождение корреляционного уравнения связи и выявление зависимости между признаками производится в следующем порядке.

Связь между результативным и факторным признаками может носить линейный и криволинейный (параболический, гиперболический, синусоидальный и т.п.) характер. При линейной форме связи используется уравнение прямой: У_х =а + bx, где У_х –теоретический уровень результативного признака;

а - начало отсчета;

х – факторный признак;

b – коэффициент регрессии, показывающий среднее изменение результативного признака при изменении факторного признака на единицу;

В случае линейной взаимосвязи результативного признака с несколькими факторами используется множественное линейное уравнение: У_х =а+вх+сх² (парабола второго порядка), У_х =а + (гипербола)

Решение корреляционного уравнения - нахождение параметров. При линейной форме связи эта система имеет вид:

,

где n-численность совокупности.

Параметры a и b можно определить по следующим формулам:

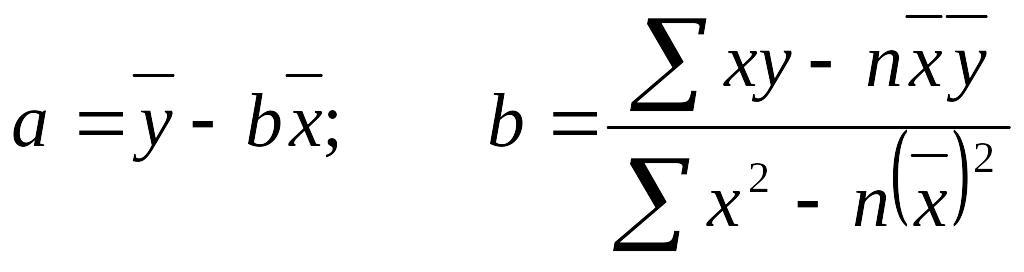
Или выразить через систему уравнений методом наименьших квадратов

В уравнении регрессии параметр а показывает усредненное влияние на результативный признак неучтенных (не выделенных для исследования) факторов, а параметр b –коэффициент регрессии показывает, насколько изменяется в среднем значение результативного признака при увеличении факторного на единицу собственного измерения.

Оценка существенности корреляции. Измерение тесноты и направления связи является важной задачей изучения и количественного измерения взаимосвязи социально-экономических явлений. Оценка тесноты связи между признаками предполагает определение меры соответствия вариации результативного признака от одного (при изучении парных признаков) или нескольких (множественных) факторов.

Теснота связи при различных формах зависимости определяется специальными показателями: при множественной линейной корреляции – коэффициентом множественной корреляции.

;

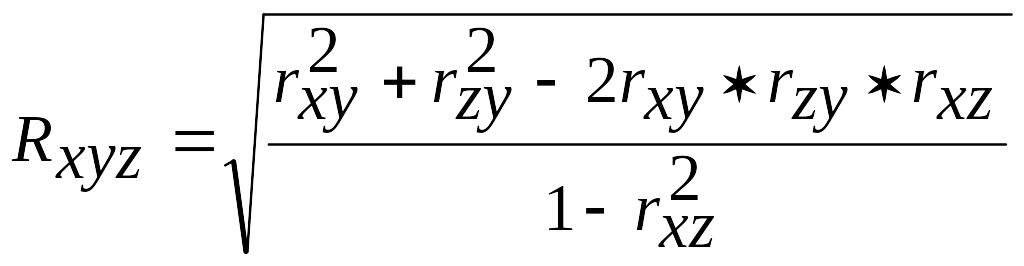при парной криволинейной зависимости – индексом корреляции

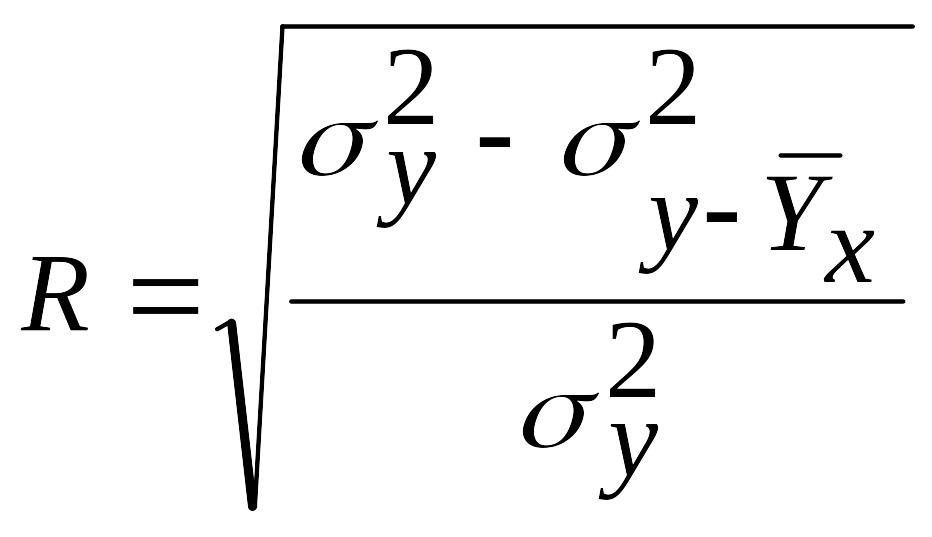при корреляционном отношении ;

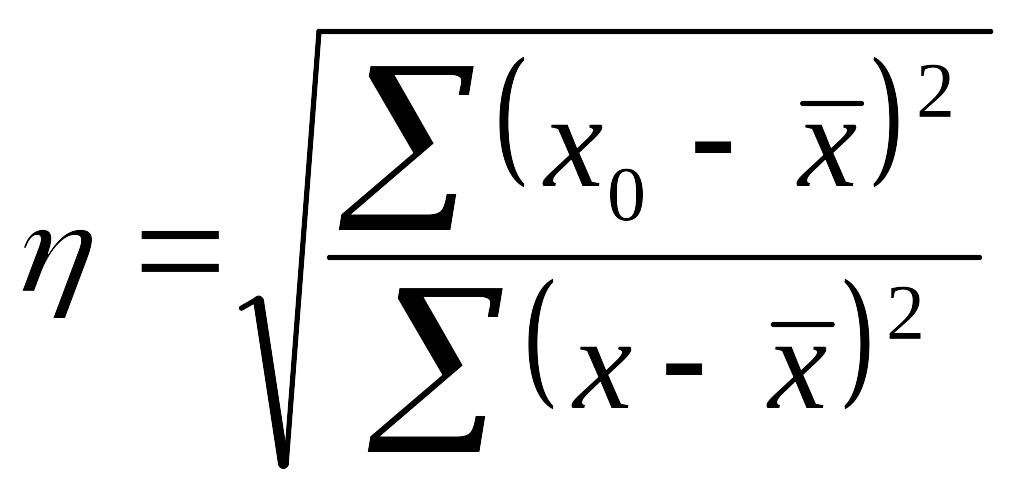При парной линейной зависимости – коэффициентом корреляции r:

,

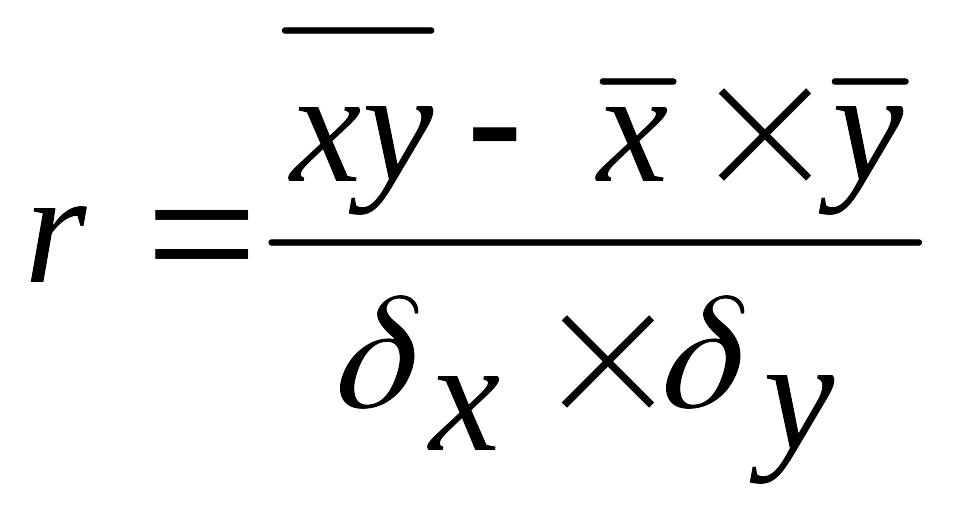где r – парный коэффициент корреляции;

- среднее произведение факторного результативного признаков;

-произведение средних размеров факторного и результативного признаков;

, -среднее квадратическое отклонение факторного и результативного признаков.

Причем, ; ; ;

; ;

; ; ;

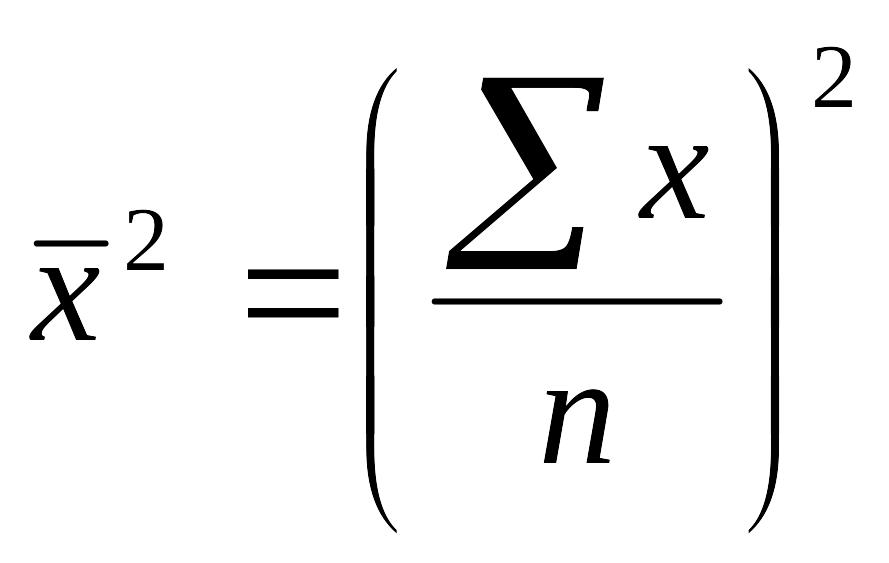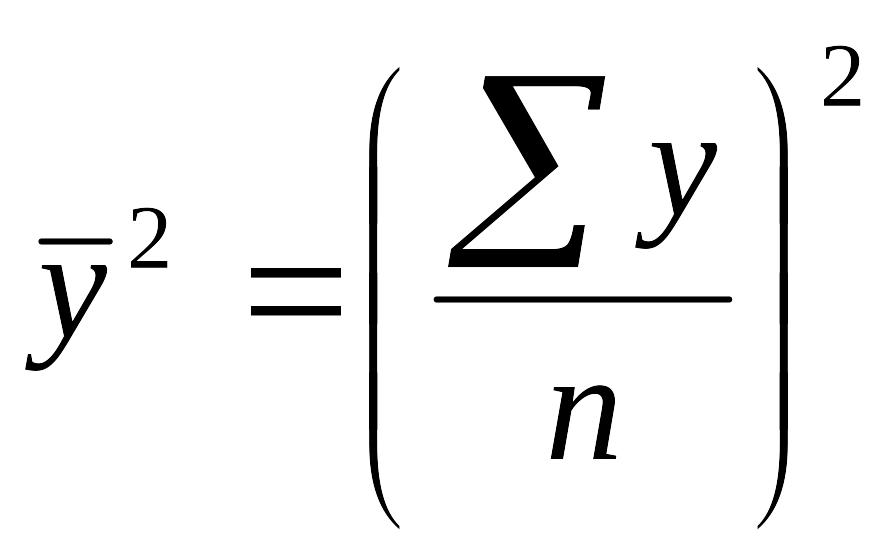
Парный коэффициент корреляции может принимать значения от –1до+1.

Если r – отрицательный, то связь обратная, а если положительный – прямая.

Причем, если r до 0,30-связь слабая,

при r от 0,30 до 0,70 – связь средняя,

при r более 0,70 –связь сильная.

Возведение в квадрат коэффициента корреляции дает коэффициент детерминации (d=r²), который позволяет сделать вывод, что доля влияния факторного признака на результативный, как минимум, равна этой величине (d).

Оценка существенности уравнения связи. Проверка адекватности модели, построенной на основе уравнения регрессии, начинается с проверки значимости каждого коэффициента регрессии и адекватности всей модели.

Проверка адекватности построенной линейной модели осуществляется с помощью расчета F-критерия Фишера. F-критерий представляет собой отношение дисперсии теоретических значений результативного признака к остаточной дисперсии, каждая из которых рассчитана на одну степень свободы. Проверяется гипотеза , о то, что выявленная зависимость у от х носит случайных характер, т.е. полученное уравнение статистически незначимо.

Где: r²-коэффициент детерминации;

n – число наблюдений;

k-число коэффициентов регрессии (при парной регрессии k=1)

Рассчитанный F-критерий сопоставляется с табличным (критическим), определяемым для числа степеней свободы (m-число параметров в уравнении; n-число наблюдений) и заданного уровня значимости . Если F_расч.>F_табл., то гипотеза о случайном характере зависимости у от х отвергается, принимается альтернативная гипотеза Н₁ – с вероятностью 0,95 можно утверждать, что выявленная зависимость у от х носит неслучайных характер, полученное уравнение статистически значимо, надежно м может быть использовано для прогноза.