3. Построение графика временной функции с распечаткой результатов

3.1.Распечатка исходных и промежуточных значений

Исходные данные:

, , .

.

Значения коэффициентов временной функции:

, , .

.

Значения коэффициентов временной функции:

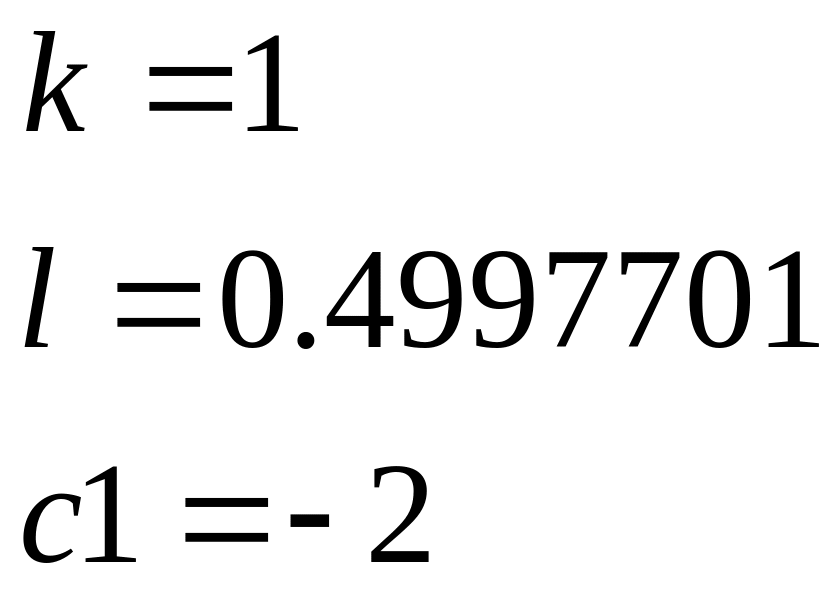
Значения временной функции:

t= 0 => Y(t)= 2

t= 0.5 => Y(t)= 1.499943

t= 1 => Y(t)= 0

t= 1.5 => Y(t)= 3.249828

t= 2 => Y(t)= 8.99954

t= 2.5 => Y(t)= 17.99914

t= 3 => Y(t)= 30.99862

t= 3.5 => Y(t)= 48.74799

t= 4 => Y(t)= 71.99725

t= 4.5 => Y(t)= 101.4964

t= 5 => Y(t)= 137.9954

t= 5.5 => Y(t)= 182.2443

t= 6 => Y(t)= 234.9931

t= 6.5 => Y(t)= 296.9918

t= 7 => Y(t)= 368.9904

t= 7.5 => Y(t)= 451.7388

t= 8 => Y(t)= 545.9871

t= 8.5 => Y(t)= 652.4854

t= 9 => Y(t)= 771.9835

t= 9.5 => Y(t)= 905.2314

t= 10 => Y(t)= 1052.979

Рисунок 3.1 – График временной функции

Заключение

Целью данного курсового проекта была разработка программы для построения графика временной функции, в которую также должны были входить подпрограммы для вычисления корней нелинейного уравнения методом простой итерации, нахождения корней системы двух линейных уравнений и функция выбора наибольшего. В процессе разработки программы пришлось охватить почти весь курс информатики, который изучался в первом семестре и часть курса по высшей математике. Все задачи, поставленные в данном курсовом проекте, были выполнены.

Список использованной литературы

1. Дьяконов В. П. Компьютер в быту. - С.:Русич, 1996 г.

2.. Ruder Jr , Millsap C. BASIC for the IBM PC: Пер. с англ. – М.: Радио и связь, 1991.

3.Пособие по математике для поступающих в ВУЗы./Под ред. Г.Н. Яковлева. – М.: Наука, 1985.

4. Алиев В.К. Языки BASIC “СОЛОН - P” М., 2000.

Приложение

Листинг программы

REM basic

SCREEN 12

DATA 1,-2,-8,0,10,.5,1,.001,.5

READ a, b, c, t0, tkon, tk, k, E, xo

l = SIN(30 * 3.14 / 180)

m = ABS(k - l)

GOSUB 1000

GOSUB 2000

GOSUB 3000

GOSUB 4000

GOSUB 8000

END

1000 REM kvadratnoe uravnenie

d = b ^ 2 - 4 * a * c

ON SGN(d) + 2 GOTO 1050, 1060, 1070

1050 REM d<0

x1 = -b / (2 * a)

x2 = SQR(ABS(d)) / (2 * a)

1060 REM d=0

x1 = -b / (2 * a)

x2 = x1

1070 REM d>1

x1 = (-b + SQR(d)) / 2

x2 = (-b - SQR(d)) / 2

IF ABS(x1) <= ABS(x2) THEN c1 = x1 ELSE c1 = x2

RETURN

2000 REM Metod Nytona

x = x0

IF x0 = 0 THEN x = x0 + E * .1

2002 Fx = x ^ 2 - SIN(5 * x)

F1x = 2 * x - 5 * COS(5 * x)

Z = Fx / F1x

x = x - Z

IF ABS(Z) > E THEN GOTO 2002

q = x

RETURN

3000 REM Gorner

a(1) = k

a(2) = l

a(3) = m

a(4) = q + c1

y = a(1)

FOR i = 2 TO 4

y = y * t + a(i)

NEXT i

y = ABS(y)

RETURN

4000 REM vibor varianta postroenia grafika

CLS

PRINT "Kakim metodom narisovat grafik"

PRINT " 1)real time"

PRINT " 2)machine time"

INPUT "Ukazhite metod", v

IF (v <> 1) AND (v <> 2) THEN GOTO 4000

4010 REM opredelenie otstupov

a0 = 53: x0 = a0

b0 = 63: y0 = 480 - b0

4020 REM opredelenie mashtaba

Mx = (640 - .02 * x0) * 5 / tkon / 6

My = (460 - y0) / y / 35

4030 REM osi koordinat

CLS

LINE (a0, b0 - 25)-(a0, y0), 6

LINE (a0, y0)-(640 - a0 + 10, y0), 6

PSET (a0, b0 - 25): DRAW "NF4G4"

PSET (640 - a0 + 10, y0): DRAW "NH4G4"

4040 REM vertik razmetka

FOR i = a0 TO 640 - x0 STEP Mx / 2

FOR j = b0 TO y0 STEP 5

PSET (i, j), 6

NEXT j

NEXT i

4050 REM gorinont razmetka

FOR j = b0 TO y0 STEP y0 / tkon / 2

FOR i = a0 TO 640 - x0 STEP 4

PSET (i, j), 6

NEXT i

NEXT j

4055 REM chislovaia razmetka

LOCATE 27, 6: PRINT "0"

LOCATE 3, 5: PRINT "y"

LOCATE 27, 76: PRINT "t,c"

LOCATE 25, 4: PRINT ; a(4)

t = 8: GOSUB 3000: LOCATE 23, 1: PRINT ; y

t = 15: GOSUB 3000: LOCATE 16, 1: PRINT ; y

t = 20: GOSUB 3000: LOCATE 5, 1: PRINT ; y

LOCATE 27, 23: PRINT "2.5"

LOCATE 27, 41: PRINT "5"

LOCATE 27, 56: PRINT "7.5"

LOCATE 27, 73: PRINT "10"

LINE (390, y0 + 33)-(390 + y0 / tkon, y0 + 33), 2

LOCATE 28, 50: PRINT "y="

t = 8: GOSUB 3000: y1 = y

t = 10: GOSUB 3000: y2 = y

ysr = y2 - y1 / 2

LOCATE 28, 52: PRINT ; ysr

4060 REM opredelenie varianta postroenia grafika

IF v = 1 THEN GOTO 5000 ELSE GOTO 6000

5000 REM real time

FOR t = t0 TO tkon STEP tk

GOSUB 3000

IF (396 - My * y) >= 63 THEN

CIRCLE (x0 + Mx * t, 396 - My * y), 3, 4

END IF

NEXT t

GOSUB 7000

6000 REM machine time

FOR t = t0 TO tkon STEP (tkon / 10 / 640)

GOSUB 3000

IF (396 - My * y) >= 63 THEN

PSET (x0 + Mx * t, 396 - My * y), 2

END IF

NEXT t

SLEEP

RETURN

7000 REM taimer

FOR taim = 1 TO 1000

taim = taim + EXP(1)

NEXT taim

RETURN

8000 REM vivod results

CLS

PRINT "koef function"

PRINT "k="; k

PRINT "l="; l

PRINT "q="; q

PRINT "c1="; c1

PRINT "m="; m

PRINT "Znachenia t and y"

FOR t = t0 TO tkon STEP tk

GOSUB 3000

PRINT "t="; t, "y="; y

NEXT t

RETURN