
- •Раздел 1. Методы оценивания параметров статистических моделей.
- •Генеральная совокупность и выборка. Способы отбора.
- •1.3. Вычисление выборочных характеристик.
- •1.4. Точечные и интервальные оценки.
- •1.5. Статистическая гипотеза и этапы её проверки.
- •Этапы проверки гипотезы:
- •1. Гипотеза о нормальном распределении генеральной совокупности.
- •2.Гипотеза о неизвестном математическом ожидании нормального распределения.
- •3. Гипотеза о равенстве математических ожиданий.
- •4. Гипотеза о равенстве дисперсий.
- •5. Гипотеза о численном значении доли ( вероятности ).
- •6. Гипотеза о равенстве долей (вероятностей).
- •Раздел 2. Корреляционный анализ.
- •2.1. Взаимосвязи экономических переменных.
- •2.2. Виды и формы корреляционных связей.
- •2.3. Оценка уравнения парной регрессии.
- •Решение:
- •Раздел 4. Анализ временных рядов.
- •4.1. Временные ряды и их характеристики.
- •4.2. Решение типовых задач.
- •Решение:
- •Решение:
- •Литература
1.4. Точечные и интервальные оценки.
Точечные оценки и их свойства.
В предыдущей теме мы рассматривали выборочную среднюю, выборочную дисперсию и выборочное среднее квадратическое отклонение, как приближенные значения соответствующих генеральных характеристик.
Выборочная характеристика, используемая в качестве приближенного значения неизвестной генеральной характеристики, называется ее точечной статистической оценкой.
«Точечная»- означает, что оценка представляет собой точку на числовой оси.
«Статистическая»- что оценка рассчитывается по результатам статистических наблюдений.
Обозначим через
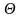 некоторую
генеральную характеристику. Ее
приближенное числовое значение можно
вычислить, используя некоторый алгоритм
или формулу по результатам выборочных
данных.
некоторую
генеральную характеристику. Ее
приближенное числовое значение можно
вычислить, используя некоторый алгоритм
или формулу по результатам выборочных
данных.
любого
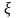 >0
lim P( I
>0
lim P( I
 n
-
I
<
)
=1.
n
-
I
<
)
=1.
n
Таким образом, чем больше объем выборки, тем оценка более состоятельна.
Оценка n генеральной характеристики называется несмещенной, если для любого n = f(x1,x2,...,xn)
Возникает вопрос: «Как хорошо выбрано приближение?»
Так как x1,...,xn – случайные величины, то и точечные оценки – величины случайные. Чтобы точечную оценку можно было считать хорошим приближением, сформулируем свойства, которыми она должна обладать: состоятельности, несмещенности и эффективности.
Оценка n генеральной характеристики называется состоятельной, если для фиксированного числа наблюдений выполняется равенство M( n)= .
Несмещенная оценка генеральной характеристики называется эффективной, если она среди всех прочих несмещенных оценок обладает наименьшей дисперсией.
Чтобы выяснить, является ли оценка эффективной, необходимо иметь минимум, с которым можно сравнивать. Часто этот минимум хорошо известен:
Нормальный закон распределения:
minM =
2/n,
min
=
2/n,
min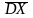 =2
4/n
=2
4/n
Задача 1.3.
Пусть генеральную совокупность образуют 5 чисел: -2;-1;0; 6; 2.
Требуется:
Вычислить генеральное среднее и генеральную дисперсию;
Составить все возможные выборки с возвратом объема n=2;
Для каждой из них вычислить значение выборочной средней и выборочной дисперсии;
Установить свойства выборочных характеристик.
Решение:
Построим ряд распределения СВ:
Х |
-2 |
-1 |
0 |
2 |
6 |
Р |
1/5 |
1/5 |
1/5 |
1/5 |
1/5 |
ДХ=8
Выборка х1 х2 |
Р(х1х2) |
= |
( )2
|
= |
|
-2 -2 |
1/25 |
-2 |
4 |
4 |
0 |
-2 -1 |
1/25 |
-1,5 |
2,25 |
2,5 |
0,25 |
-2 0 |
1/25 |
-1 |
1 |
2 |
1 |
-2 2 |
1/25 |
0 |
0 |
4 |
4 |
-2 6 |
1/25 |
2 |
4 |
20 |
16 |
-1 -2 |
1/25 |
-1,5 |
2,25 |
2,5 |
0,25 |
-1 -1 |
1/25 |
-1 |
1 |
1 |
0 |
-1 0 |
1/25 |
-0,5 |
0,25 |
0,5 |
0,25 |
-1 2 |
1/25 |
0,5 |
0,25 |
2,5 |
2,25 |
-1 6 |
1/25 |
2,5 |
6,25 |
18,5 |
12,25 |
0 -2 |
1/25 |
-1 |
1 |
2 |
1 |
|
1/25 |
-0,5 |
0,25 |
0,5 |
0,25 |
0 0 |
1/25 |
0 |
0 |
0 |
0 |
0 2 |
1/25 |
1 |
1 |
2 |
1 |
0 6 |
1/25 |
3 |
9 |
18 |
9 |
2 -2 |
1/25 |
0 |
0 |
4 |
4 |
0 -1 |
1/25 |
0,5 |
0,25 |
2,5 |
2,25 |
2 0 |
1/25 |
1 |
1 |
2 |
1 |
2 2 |
1/25 |
2 |
4 |
4 |
0 |
2 6 |
1/25 |
4 |
16 |
20 |
4 |
6 -2 |
1/25 |
2 |
4 |
20 |
16 |
6 -1 |
1/25 |
2,5 |
6,25 |
18,5 |
12,25 |
6 0 |
1/25 |
3 |
9 |
18 |
9 |
6 2 |
1/25 |
4 |
16 |
20 |
4 |
6 6 |
1/25 |
6 |
36 |
36 |
0 |
Построим ряд распределения выборочной средней:
|
-2 |
-1,5 |
-1 |
-0,5 |
0 |
0,5 |
1 |
2 |
2,5 |
3 |
4 |
6 |
Р |
1/25 |
2/25 |
3/25 |
2/25 |
3/25 |
2/25 |
2/25 |
3/25 |
2/25 |
2/25 |
2/25 |
1/25 |
М =
1,так как генеральная средняя МХ=1,то
значит
=
1,так как генеральная средняя МХ=1,то
значит
 -
несмещенная оценка математического
ожидания.
-
несмещенная оценка математического
ожидания.
Построить ряд распределения выборочной дисперсии:
D
|
0
|
0.25
|
2.25
|
1
|
4
|
12.25
|
9
|
16
|
Р |
5/25 |
4/25 |
2/25 |
4/25 |
4/25 |
2/25 |
2/25 |
2/25 |
М( D ) = 4, а генеральная дисперсия DХ = 8 , то значит D - смещенная оценка дисперсии.
Доказано, что выборочное среднее является несмещенной и состоятельной оценкой математического ожидания генеральной совокупности, а выборочная дисперсия является смещенной оценкой дисперсии. Иными словами , выборочная дисперсия оценивает генеральную дисперсию с недостатком, поэтому в качестве оценки генеральной дисперсии удобнее брать исправленную дисперсию:
S2
=
Исправленная дисперсия является несмещенной и состоятельной оценкой генеральной дисперсии случайной величины Х.
Интервальные оценки числовой характеристики случайной величины.
После получения точечной оценки
желательно иметь данные о надёжности
такой оценки. Особенно важно иметь
сведения о точности оценок для небольших
выборок (поскольку с возрастанием объёма
выборки состоятельность и несмещенность
основных оценок гарантируется
утверждениями математической статистики).
Поэтому точечная оценка может быть
дополнена интервальной оценкой –
интервалом ( ;
;
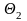 ),
где
=
-
),
где
=
-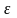 ,
=
+
,
внутри которого с наперед заданной
вероятностью
,
=
+
,
внутри которого с наперед заданной
вероятностью
 находится точное значение оцениваемого
параметра
.Задачу
определения такого интервала называют
интервальным оцениванием, а сам
интервал – доверительным интервалом.
При этом
называют доверительной вероятностью,
с которой оцениваемый параметр
попадает в интервал (
;
).
находится точное значение оцениваемого
параметра
.Задачу
определения такого интервала называют
интервальным оцениванием, а сам
интервал – доверительным интервалом.
При этом
называют доверительной вероятностью,
с которой оцениваемый параметр
попадает в интервал (
;
).
Зачастую для определения доверительного
интервала заранее выбирают число
 <
<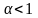 ,
называемое уровнем значимости, и
находят два числа
и
такие,
что Р(
<
<
)
= 1-
,
называемое уровнем значимости, и
находят два числа
и
такие,
что Р(
<
<
)
= 1-
 .
.
В этом случае говорят, что интервал (
 ;
)
накрывает неизвестный параметр
с вероятностью (1-
;
)
накрывает неизвестный параметр
с вероятностью (1-
 ).
Границы интервала называются
доверительными.
).
Границы интервала называются
доверительными.
Выбор
определяется конкретными условиями.
Обычно используется
 ,
что соответствует 90, 95, 99%-м доверительным
интервалам.
,
что соответствует 90, 95, 99%-м доверительным
интервалам.
Общая схема построения доверительного интервала:
По сделанной выборке находится точечная оценка неизвестного параметра .
Задаются надёжностью .
По определённым правилам находят такое число >0 (ошибка выборки), чтобы выполнялось соотношение Р ( 1< <
 )
=
.
)
=
.
Поскольку выборочная совокупность представляет собой лишь часть генеральной совокупности, то выборочные характеристики не будут точно совпадать с генеральными.
Формулы расчета ошибки выборки случайного отбора
-
Выборка с повтором
Бесповторная выборка
Для средней
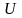

U
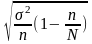
Для доли
U
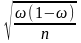
U

где
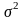 -
выборочная дисперсия;
-
выборочная дисперсия; -
доля значения признака; n
–объём выборки;N
–объём генеральной совокупности;
-
доля значения признака; n
–объём выборки;N
–объём генеральной совокупности;
Если объём выборки более 30 , то U находят по функции Лапласа, а если не более 30 – то по распределению Стьюдента (см. приложения).
Задача 1.4.
С помощью случайного повторного отбора руководство фирмы провело выборочное обследование 900 своих служащих. Средний стаж работы в фирмы- 8,7 года, среднее квадратическое отклонение- 2,7 года. Среди обследованных оказалось 270 женщин. Считая стаж работы распределенным по нормальному закону определить:
а) С вероятностью 0,95 доверительный интервал, в котором окажется средний стаж работы всех служащих в фирме;
б) С вероятностью 0,9 доверительный интервал, накрывающий неизвестную долю женщин в коллективе.
Решение:
а)
N=900 > 30;
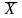 =
8,7;
=
8,7;
 =2,7;
=2,7;
 .
.
U =
1,64;
=
1,64;
 ;
;
Доверительный интервал среднего стажа работы ( 8,7 – 0,1476; 8,7 + 0,1476) или ( 8,5524; 8,8476).
б)
N = 900; n = 270
;
 ;
;
U
=1.28;
 0.0196;
0.0196;
Доверительный интервал доли женщин в коллективе (0,3-0,0196;0,3+0,0196) или (0,2904;0,3196).
Задача 1.5.
Владелец автостоянки опасается обмана со стороны своих служащих.В течение года (365 дней) им проведено 40 проверок. По данным проверок в среднем число автомобилей на стоянке составило 400 единиц, а среднеквадратическое отклонение 10 единиц. Считая отбор случайным, с вероятностью 0,99 оценить с помощью доверительного интервала истинное среднее число автомобилей, оставленных на стоянке. Обоснованы ли опасения владельца стоянки, если по отчетности охранников число автомобилей, оставленных под охрану в среднем составляет 395 единиц.
Решение:
Произведена выборка без повторения, так как нет смысла в течение одних суток делать повторную выборку.
n=40<30; N=365;
=400;
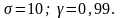
U
=
2.32;
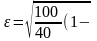
 =4.058;
=4.058;
Доверительный интервал среднего числа автомобилей оставленных на стоянке (395,942;404,058).
Так как данные отчетности охранников ( 395 единиц ) не входят в данный интервал, то с уверенностью 99% можно ожидать, что работники автостоянки обманывают владельца.
Задача 1.6.
Служба контроля Энергосбыта провела выборочную проверку расхода электроэнергии жителями одного из многоквартирных домов. Было выбрано 10 квартир (таблица случайных чисел) и определен расход электроэнергии в течении одного из летних месяцев (кВт.ч.):
125;78;102;140;90;45;50;125;115;112.
Свероятностью0,95 определить доверительный интервал для оценки среднего расхода электроэнергии на одну квартиру в доме, при условии, что в доме 70 квартир. Отбор бесповторный.
Решение:
n=10>30;
= ;
;
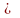 S2=
S2= =
1033.
=
1033.
,
k= n-1= 9,
 =
2,26;
= 2,26*
=
2,26;
= 2,26* =21.27.
=21.27.
Доверительный 95%-ный интервал среднего расхода электроэнергии ( 76,93; 119,47).
Упражнения и задачи.
1. Приведена статистика по годовым темпам (%) инфляции в стране за последние 10 лет:
2.8; 3,2; 5,1; 1,8; -0,6; 0,7; 2,1; 2,7; 4,1; 3,5.
Найти несмещенные оценки среднего темпа инфляции, дисперсии и среднего квадратического отклонения .
2. На основании наблюдений за работой 25 кандидатов на должность секретаря-референта установлено, что в среднем они тратили 7 минут на набор одной страницы сложного текста на компьютере при выборочном стандартном отклонении 2 минуты. Определите 95%-ный доверительный интервал для среднего времени набора.


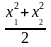
 =
2-
(
)2
=
2-
(
)2