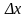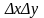Решение:

Обозначим расходы на товар А через у, а доходы на одного члена семьи – х.

Ежегодные абсолютные приросты определим по формуле:

1. Оформим расчеты в виде таблицы:

Таблица 1.

уt		xt
30	-	100	-
35	5	103	3
39	4	105	2
44	5	109	4
50	6	115	6
53	3	118	3
	23		13

Значения не имеют четко выраженной тенденции, они варьируют вокруг среднего уровня, следовательно, это означает наличие в ряде динамики линейного тренда.

2. Так как ряды динамики имеют общую тенденцию к росту, то для построения регрессивной модели спроса на товар А в зависимости от дохода, необходимо устранить тенденцию. С этой целью модель может строиться по первым разностям уровней:

, если ряд характеризуется линейной тенденцией.

3. Итак, модель имеет вид:

Для определения параметров a и b применяется МНК:

Для решения системы составим расчетную таблицу:

Таблица 2.

3	9	5	15
2	4	4	8
4	16	5	20
6	36	6	36
3	9	3	9
0	0	0	0

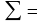Подставив соответствующие суммы в систему, и решив ее, имеем: a=2,56; b=0,56;

Таким образом, линейное уравнение регрессии первых уровней динамических рядов имеет вид:

4. Коэффициент регрессии 0,56 показывает, что с ростом прироста душевого дохода на 1% расходы на товар А увеличиваются в среднем на 0,56 руб.

5. Включив фактор времени, модель имеет вид: y=a+bx+ct.

Применив МНК, получим систему:

Оформим расчеты в таблицу:

Таблица 3.

t	e	x	yx	yt	xt	x2	t2
1	30	100	3000	30	100	10000	1
2	35	103	3605	70	206	10609	4
3	39	105	4095	117	315	11025	9
4	44	109	4796	176	436	11881	16
5	50	115	5750	250	575	13225	25
6	53	118	6254	318	708	13924	36
0	0	0	0	0	0	0	0

Подставив соответствующие суммы в систему, и решив ее, имеем:

a = - 5,42; b = 0,322; c = 3,516;

Уравнение регрессии имеет вид: у= - 5,42 + 0,322х + 3,516t;

Коэффициент b = 0,322 фиксирует силу связи у и х. Он означает, что с ростом дохода на одного члена семьи на 1% расходы на товар А возрастут в среднем, на 0,322 руб. при условии неизменной тенденции роста.

Параметр с = 3,516(руб.) характеризует среднегодовой абсолютный прирост расходов на товар под воздействием других факторов при условии неизменного дохода.

Упражнения и задачи.

1. Имеются данные о разрешениях на строительство нового жилья помесячно в 2002 году, в % к уровню 1995 г.

Месяц	январь	февраль	март	апрель	май	июнь	июль	август	сентябрь	октябрь
Разрешения, % к 1995г.	86,4	87,5	80,2	84,3	86,8	86,9	85,2	85,0	87,5	90,0

Приняв гипотезу линейного тренда, состоящую в примерном постоянстве разрешений помесячно, исследовать временной ряд.

2. Имеются данные об объемах продаж в перерабатывающей промышленности и торговле в 1994 году, в сопоставимых ценах 1987 года, млрд.руб.

Месяц	январь	февраль	март	апрель	май	июнь	июль	август	сентябрь	октябрь
Объем продаж ,млрд.руб.	578,2	539,4	545,3	551,9	549,7	550,1	554,0	550,0	565,6	564,7

Исследовать временной ряд, приняв гипотезу линейного тренда о примерном постоянстве объемов продаж помесячно.

3. Имеются данные об экспорте и импорте Германии, млрд.долл.США, за 1985 – 1996г.г.

Год	Экспорт	Импорт	Год	Экспорт	Импорт
1986	184	158	1991	403	390
1986	243	191	1992	422	402
1987	294	228	1993	382	345
1988	323	280	1994	430	385
1989	341	270	1995	524	464
1990	410	346	1996	521	456

1. Определить ежегодные приросты и сделать выводы о тенденции развития каждого ряда;

2. Построить линейную модель одного из факторов (выбрать самостоятельно), используя первые разности исходных динамических рядов;

3. Пояснить экономический смысл коэффициента регрессии;

4. Построить линейную модель этого фактора, включив в нее фактор времени. Интерпретировать полученные результаты.

5. Построить столбчатую диаграмму изучаемых показателей.

Вопросы для самопроверки:

1. Предмет и задачи дисциплины.

3. Точечная оценка случайной величины и ее свойства.

4. Интервальная оценка случайной величины и этапы ее нахождения.

5. Ошибка выборки. Средняя ошибка выборки.

6. Формулы расчета ошибки выборки с повтором.

7. Формулы расчета ошибки выборки без повтора.

8. Статистическая гипотеза. Этапы ее проверки.

9. Понятие нулевой и альтернативной гипотезы.

10. Ошибки статистических гипотез.

11. Статистический критерий.

12. Критическая область.

13. Принятие статистической гипотезы.

14. Метод наименьших квадратов.

15. Метод максимального правдоподобия.

16. Функциональная, статистическая и корреляционная зависимость.

17. Задачи корреляционного анализа.

18. Пути возникновения корреляционной зависимости.

19. Методы оценки корреляционной зависимости.

20. Показатель Фехнера и его недостатки.

21. Линейный коэффициент корреляции Пирсона и его недостатки.

22. Линейный коэффициент корреляции и его смысл.

23. Коэффициент детерминации и его смысл.

24. Линейная функция регрессии и интерпретация его параметров.

25. Задача парной корреляции.

26. Задача дисперсионного анализа. Однофакторный дисперсионный анализ.

27. Задача двухфакторного дисперсионного анализа.

28. Временные ряды и их характеристики.

30.Основные задачи анализа временных рядов.