Задание на уирс

1. Дополнительные теоретические сведения. Уравнение баланса энергии

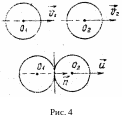
Опыт показывает, что время удара шарика о плиту зависит от его скорости. Найдем эту зависимость. Рассмотрим удар двух тел, движущихся по линии, соединяющей их центры инерции (О₁ и О₂) со скоростями и . Относительная скорость тел будет

= – (6)

и движение можно рассматривать в системе координат, движущейся со скоростью (рис. 4). В некоторый момент времени тела коснутся друг друга, при этом направлении нормали к плоскости касания параллельно относительной скорости. Если нормаль проходит через центры инерции, то произойдет явление прямого центрального удара. Тела начнут деформироваться, при этом часть кинетической энергии относительного движения перейдет в потенциальную энергию деформации, другая часть в энергию упругих волн, распространяющихся по обоим телам от места соударения.

Промежуток времени, в течение которого тела касаются друг друга, назовем временем удара τ. Очевидно, что τ = τ₁ + τ₂, где τ₁ – длительность первого акта удара (от момента касания до момента наибольшего сжатия тел); τ₂ – длительность второго акта (от момента наибольшего сжатия до момента рассоединения тел). В случае абсолютно упругого удара (без диссипации энергии механического движения) . Поэтому для анализа явления удара достаточно рассмотреть только первую половину удара.

Обозначим массы тел через т₁ и т₂, тогда общая скорость в момент наибольшего сжатия по закону сохранения импульса будет

. (7)

К этому моменту времени кинетическая энергия системы уменьшится на величину

. (8)

Назовем величину х = ε₁ + ε₂ сближением тел в произвольный момент времени t (внутри интервала 0<t<τ₁), где ε₁ и ε₂ – абсолютные деформации тел вдоль линии удара, и относительной скоростью сближения величину

. (9)

Тогда потерянная системой кинетическая энергия от момента t до момента t = τ₁ будет

. (10)

В уравнении (10) учтено, что массы областей деформации Δт_1,2 << т_1,2 ­ масс соударяющихся тел и что протяженность областей деформации ε₁ и ε₂ много меньше протяженности тел вдоль линии удара.

Кинетическая энергия, потерянная при движении от момента первого касания (t = 0) до момента t

. (11)

Одна часть этой энергии перешла в потенциальную энергию деформации П, другая – в энергию упругих колебаний Е, и уравнение баланса энергии системы имеет вид

ΔТ = П + Е. (12)

Обозначим через F упругую силу давления одного тела на другое, тогда

. (13)

На основе решения основных уравнений упругого равновесия, учитывающих все виды деформаций, Г. Герц показал, что для абсолютно упругого удара двух шаров в квазистатическом приближении

F = k · x^3/2 и , (14)

где k = const, определяемая выражением

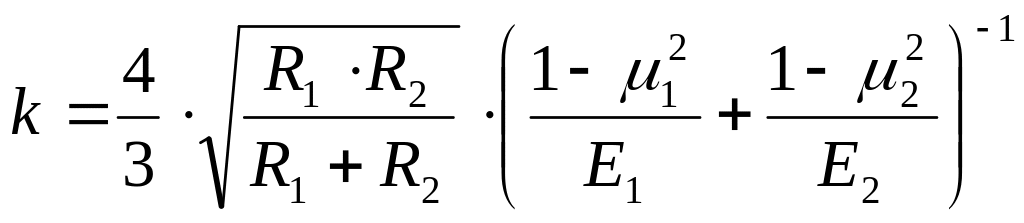. (15)

Здесь Е₁ и Е₂ – модули Юнга, μ₁ и μ₂ – коэффициенты Пуассона, R₁ и R₂ – радиусы шаров.

Если материал соударяющихся тел одинаково: Е₁ = Е₂ = Е, μ₁ = μ₂ = μ, а R₂→∞ (удар шара о плоскость), то постоянная k принимает вид

. (16)

Тогда уравнение (12) может быть переписано в виде

. (17)

Релей [2] показал, что отношение энергии Е к кинетической энергии системы определяется равенством

. (18)

Поскольку скорость звука υ_зв >> υ, то, как следует из (18), величиной Е по сравнению с ΔT_max можно пренебречь.

В случае удара шара о стенку из того же материала, масса которой т₂ >> т₁, если принять, т₁ = т₂, уравнение баланса энергии (17) преобразуется к виду

или . (19)

В момент окончания первого акта удара скорость относительного сближения тел х обращается в нуль, х = 0 тогда, как видно из (19) и (14), максимальное значение сближения и наибольшая упругая сила, действующая на тела, будут иметь значения

, . (20)