ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ

Государственное образовательное учреждение

высшего профессионального образования

Московский технический университет связи и информатики

Волго-Вятский филиал

ЛАБОРАТОРНАЯ РАБОТА №1–1

Механический удар

для студентов по направлению «Телекоммуникации»

Нижний Новгород 2008

ЛАБОРАТОРНАЯ РАБОТА

Механический удар

Составитель Б.М. Горюнов.

Научный редактор Н.Ф. Перепеченков

Издание одобрено на заседании кафедры «___» _____________ 200__ г.

Протокол № ____

Цель работы: ознакомиться с элементами теории механического удара и экспериментально определить время удара τ, среднюю силу удара F, коэффициент восстановления ξ.

Практическая ценность работы: в работе изучается экспериментальный метод измерения временных интервалов порядка 10^-5 с, а также методы обработки экспериментальных данных.

Теоретическая часть

1. Основные характеристики удара

Ударом называется изменение состояния движения тела вследствие кратковременного взаимодействия его с другим телом. Во время удара оба тела претерпевают изменения формы (деформацию).

Сущность удара заключается в том, что кинетическая энергия относительного движения соударяющихся тел за короткое время преобразуется в энергию упругой деформации и в той или иной степени в энергию молекулярного движения. В процессе удара происходит перераспределение энергии между соударяющимися телами.

Процесс удара можно разделить на две фазы. В течение первой фазы происходит сближение тел: при этом кинетическая энергия системы тел уменьшается, относительная скорость убывает до нуля. Вслед за этим наступает вторая фаза удара: тела начинают удаляться друг от друга, восстанавливая свою форму, кинетическая энергия и относительная скорость возрастают. Когда тела отдаляются, процесс удара заканчивается.

Н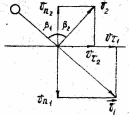 аблюдения показывают, что относительная скорость после удара не достигает своей прежней численной величины. Это объясняется тем, что на практике мы никогда не имеем дело с идеально жесткими телами и идеально гладкими поверхностями.

П

Рис. 1

усть на поверхность падает шар с некоторой скоростью и отскакивает от нее со скоростью (рис. 1). Обозначим: , , , – нормальные и тангенциальные составляющие скоростей и , а β₁ и β₂ – соответственно углы падения и отражения. В идеальном случае, при абсолютно упругом ударе и идеально гладкой поверхности, нормальные составляющие скорости падения и отражения и их касательные составляющие были бы равны = ; = . Это означало бы, что скорость шара до удара равна его скорости после удара = , а также угол падения равен углу отражения β₁=β₂. В условиях реального удара всегда происходит потеря энергии, вследствие чего как нормальные, так и тангенциальные составляющие скорости после удара уменьшаются: < ; < . Отношение численной величины нормальной составляющей относительной скорости после ударе к ее величине до удара есть физическая характеристика, зависящая от природы сталкивающихся тел,

. (1)

Эту характеристику ε называют коэффициентом восстановления. Числовое значение его лежит между 0 и 1.

2. Определение средней силы, начальной и конечной скоростей шарика при ударе

Экспериментальная установка состоит из стального шарика А, подвешенного на проводящих нитях, и неподвижного тела В большой массы, с которой шарик соударяется (рис. 2). Угол отклонения подвеса α измеряется 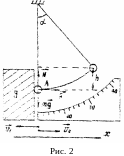по шкале. В момент удара на шар массой т действует сила тяжести со стороны Земли , сила реакции со стороны нити , средняя сила удара со стороны тела В. На основании теоремы об изменении импульса материальной точки

т( – ) = ( + + )τ, (2)

где и – векторы скоростей шара до и после удара; τ – длительность удара.

После проектирования уравнения (2) на горизонтальную ось х определим среднюю силу удара F:

. (3)

Скорости шарика и определяются на основании теоремы об изменении механической энергии системы «шар–Земля». Изменение механической энергии системы определяется суммарной работой всех внешних и внутренних непотенциальных сил. Поскольку внешняя сила , перпендикулярна перемещению и нить нерастяжима, то эта сила работу не совершает, внутренняя же сила потенциальна, поэтому энергия системы «шар–Земля» не меняется,

. (4)

Из чертежа (рис. 2) следует, что и тогда из уравнения (4) получим значения начальной и конечной скоростей шарика:

. (5)