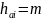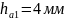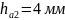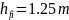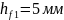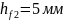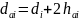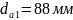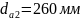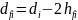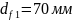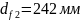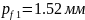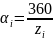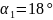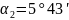8. Розрахунок одноступеневого зубчастого редуктора

Спочатку оберемо кількість зубців колеса та шестерні взявши стандартні значення з ГОСТ 13733-77. При цьому має виконуватись умова:

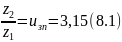
Найбільш прийнятними є числа 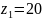, 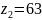. Далі оберемо модуль зубчастої передачі за ГОСТ 9563-60; виходячи з того, що передача має бути достатньо компактною приймаємо .

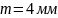За обраним модулем розраховуємо ділильні діаметри колеса та шестерні:

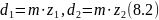
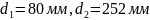
Розраховуємо міжосьову відстань за формулою:

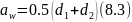
Основні параметри шестерні та колеса для зазначених модуля та діаметрів приведені в таблиці 1.3.

Таблиця 8.1.

Назва параметру	Формула розрахунку	Значення для шестерні	Значення для колеса
Висота головки зубця
Висота ніжки зубця
Діаметр вершин зубців
Діаметр впадин зубців
Радіус кривизни перехідної кривої
Крок між сусідніми зубцями

9. Порядок побудови евольвенти

1. Будуємо ділильні кола двох коліс по відомим діаметрам таким чином, щоб вони дотикались. Також будуємо кола вершин та впадин зубців для обох коліс. Сполучаємо їхні центри лінією, до якої будуємо перпендикуляр в точці дотику. Результат показано на рис. 9.1.

Рис. 9.1. Побудова ділильних кіл, кіл вершин та впадин зубців

2. Під кутом в 20° до перпендикуляру будуємо пряму (нормаль зачеплення). Після цього будуємо коло, що є дотичним до нормалі, а центр якого співпадає з центром колеса – основне коло (рис. 9.2.).

Рис. 9.2. Побудова нормалі та основного кола шестерні

3. Відстань між точкою дотику основного кола до нормалі та центром зачеплення поділяємо на чотири рівні відрізків. Кінці відрізків переносимо на основне коло, перемістивши їх по дугам, що мають центр в точці дотику основного кола до нормалі. На рис. 9.3. дуги замінено на концентричні кола, що перетинають основне коло в необхідних для подальшої побудови точках.

Рис. 9.3. Перенесення кінців рівних відрізків нормалі на основне коло

4. В точках перетину основного кола з концентричними будуємо дотичні до основного кола (рис. 9.4.).

Рис. 9.4. Побудова дотичних до основного кола в точках його перетину з концентричними колами

5. На дотичних відкладаємо відстані, що дорівнюють довжині відповідних відрізків на нормалі. Утворені точки сполучаємо кривою, що і є шуканою евольвентою (рис. 9.5.)

Рис. 9.5. Побудова евольвенти

6. Відтворюємо профіль евольвенти, дзеркально відобразивши його відносно осі зуба. З'єднуємо профілі з колом западин кривою відповідного радіуса.

Рис. 9.6. Завершення побудови профілю зуба

7. Розмножуємо отриманий профіль зуба в необхідній кількості. Повторюємо вказаний алгоритм для побудови профілю зубців веденого колеса.

10. Розрахунок швидкохідного вала редуктора на статичну міцність

Для розрахунку необхідно знати діаметр вала, місця розташування опор, шківа, зубчастого колеса, їхні діаметри, а також обертальний момент на даному валу.

Побудуємо схему вала та вкажемо силові фактори, що діють на вал (рис 10.1).

Рис. 10.1. Схема швидкохідного вала редуктора

На схемі точки A і B – опори вала, точки O₁ та O₂ – центри веденого шківа та зубчатого колеса відповідно. На вал діє момент T, який обчислюємо за формулою:

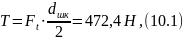
де 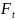– колова сила, обчислена за формулою 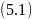, 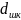– діаметр веденого шківа.

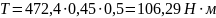
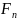– сила від натягу паса, що діє на вал та підшипники, обчислена за формулою . 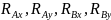– реакції, що виникають в опорах вала. 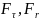– тангенціальна та радіальна сили відповідно.

Спочатку знайдемо сили 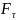та 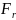, що виникають в зубчастому зачепленні.

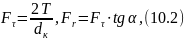
де 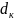– ділильний діаметр зубчастого колеса, 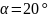– кут зачеплення зубчастої передачі.

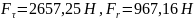
Далі розраховуємо реакції в опорах вала за формулами, отриманими з використанням методів теоретичної механіки:

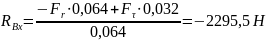
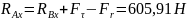
Знак «-» означає обернений напрямок реакції до того, що зображений на схемі. Отримавши значення реакцій в опорах побудуємо епюри моментів від сил , та і визначимо найбільш напружену ділянку вала (рис.10.2.). Відповідно до побудованих епюр, найбільш напруженою є ділянка під зубчастим колесом. Розрахуємо максимальний момент в точці O₂:

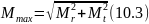
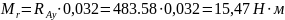
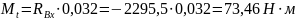
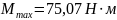
Рис. 10.2 Епюри моментів, що діють на вал

В перерізі вала, що відповідає точці O₂ , діють напруження згину 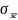та дотичні напруження 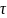, які необхідно замінити на еквівалентне. Спочатку розрахуємо складові еквівалентного напруження за формулами:

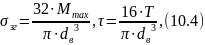
де 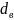– діаметр вала.

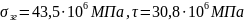
Еквівалентне напруження розраховуємо за формулою:

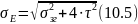
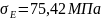
Перевіримо умову статичної міцності:

Матеріалом вала оберемо сталь 45, отже 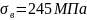. Підставимо отримані значення в умову 10.5 та перевіримо вал на статичну міцність:

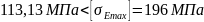
Умова виконується, отже вал витримує статичні навантаження.