24. Средняя арифметическая, основные мат св-ва.

Ср арифметические бывают простые и взвешанные. Простая вычисляется не только, когда отсутствуют веса, но и когда их трудно определить, напр для определения цен на рынке у разных продавцов. В таком случае вычисл простую среднюю и принебр погрешностью в рез-те. Это можно сделать если веса отличаются незначительно друг от друга. Если веса отличаются сильно, исп-е простой средней приведет к искажению инфы.

Средняя арифм простая:

Где х_ср – среднее значение признака

Х – индив знач-е признака у каждой ед сов-сти

n – кол-во единиц сов-сти

Если исходные данные предст в сгруппир виде, т.е. в виде рядов распр-я дискретных либо интервальных, исп среднюю арифм взвешанную.

Средняя арифм взвешанная:

Где f – частоты, т.е. веса для каждого вар-та признака, кот показ повторяемость данного признака.

Св-ва средней арифметической: 1) от увел/уменьш веса каждого вар-та в А раз, вел-на средней не меняется 2) Вел-на средней завис не от абс знач весов, а от пропорций, поэтому вместо абсол значений для взвешанной можно брать веса вар-тов, выраж либо в долях к единице, либо в %. Из этого вытекает правило расчёта средних при неизв абсол занчениях весов, а только по пропорц м/ними. 3) Если ум/увел вес вар-ты признака на некот число А, то средняя уменьшится или увел на то же число А. С пом этого св-ва можно перейти при расчётах к ряду простых чисел и рассчитать средние арифм методом отсчета от условного 0 или методом моментов

4) Ср вел-на * числ-сть всей совок-сти = сумме произведений каждого вар-та на его числ-сть. Оно исп при расчёте фондов з/п, валового сбора…

5) Сумма отклонений индив знач от их средней арифм-ой равна 0.

6) Сумма квадратов отклонений индив значений от их ср арифм меньше, чем сумма квадратов отклонений индив значений от любой др вел-ны.

При расчётах выбир та форма средней, кот соотв ф-ле расчёта данного показ-ля. Когда сущ обрат завис-сть между вел-нами, вычисл ср гармонич, если завис-сть прямая – ср арифм. В соотв с этим среднюю можно определить как вел-ну, кот не меняет знач опред показателя при подстановке в заранее составл ур-не вместо индив знач средних.

25. Средняя гармоническая и др виды средних.

1) средняя гармоническая простая:

Взвешанная:

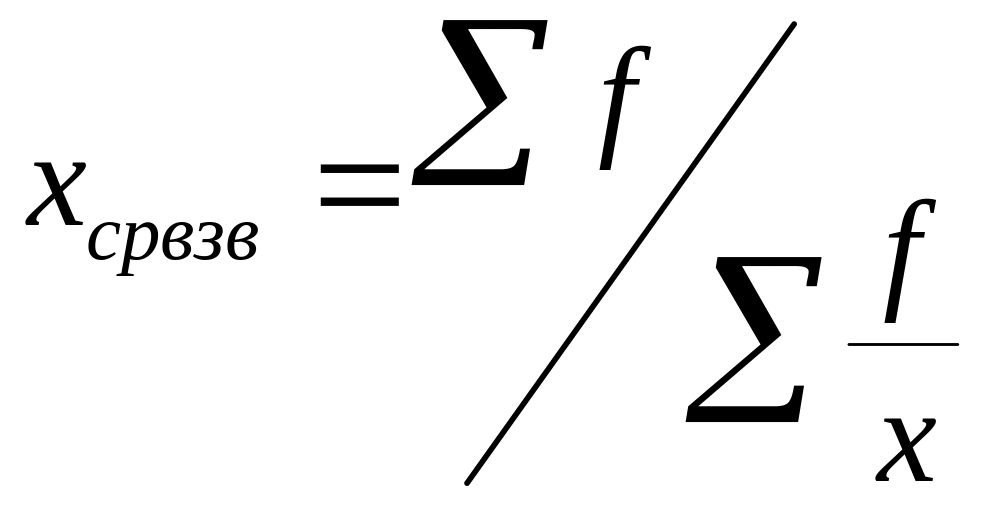
2) средняя степенная:

3) средняя геометрическая

Где П – число пи (3,14)

При расчёте ср геометрической число коэф-тов всегда на 1 меньше, чем число членов ряда. Эта ф-ла ср геом невзвешанной. Средние, перечисленные выше, как правило, явл обобщ хар-каим и в ряду не присутствуют.

26. Мода и медиана, их смысл и значение, вычисление.

Мода – вел-на признака, те.е варианта, кот встречается в ряду чаще всего.

X_мод – нижняя граница модального интервала

i – вел-на интервала

f_m, f_m-1, f_m+1 – частоты соотв-но модального, предшествующего и след за модальным интервалов Медиана – знач-е ряда, расп в его сер-не, т.е. такое знач ряда, кот делит этот ряд по числ-сти на 2 равные части.

X_me – нижняя граница модального интервала

S_m-1 – сумма накопл частот в интервалах, предшествующих медианному.

Мода и медиана – конкр вел-ны, совпад с конкр вар-тами ряда.

При построении ряда распр-я по кол-ву его членов наиболее точной ср вел-ной при анализе служит медиана. Если распр-е вел-н в ряду нормально, то мода, медиана и ср арифм по вел-не совпадают.

Если распр-е в ряду ассиметр, то соотн-я этих 3х вел-н исп при анализе как хар-ку ассиметрии.