
shpory_TViMS_asd
.docx|
1. Случайные события и их классификация. Алгебра событий. Частота и вероятность. Пространством элементарных событий называют множество взаимоисключающих исходов эксперимента такое, что каждый интересующий результат эксперимента может быть однозначно описан с помощью элементов этого множества. Элементы называются элементарными событиями и обозначаются . Событием называют любое подмножество элементов из . Событие произойдет, если произойдет какое-либо из элементарных событий . Пустое множество называется невозможным событием. Суммой двух событий и называется событие + , состоящее из элементарных событий, принадлежащих хотя бы одному из событий или . Произведением двух событий и называется событие , состоящих из элементарных событий, принадлежащих одновременно и . Противоположным событием событию называют событие , состоящее из элементарных событий, не принадлежащих . Разностью двух событий и называют событие \, состоящее из элементарных событий, которые входят в событие . События и называются несовместными , если у них нет общих элементарных событий. Пусть F - поле событий для данного эксперимента. Вероятностью P(A) называется числовая функция, определенная на всех F и удовлетворяющая трем условиям (аксиомам вероятностей): P(A) 0; P()=1; Для
любой конечной или бесконечной
последовательности наблюдаемых
событий
2. Классическое определение вероятности. Классический способ задания вероятности При данном способе пространство элементарных событий является конечным, и все элементарные события равновероятны. Тогда вероятность события определяется равенством
где
3. Статистическое определение вероятности. Пусть при проведении n испытаний некоторое событие А появилось m раз. Многочисленные эксперименты такого рода показывают , что при больших n отношение m/n, называемое частостью события А, остается примерно постоянным. При статистическом определении вероятностью события А наз-ся постоянная величина, вокруг которой колеблются значения частостей при неограниченном возрастании числа n. Статистической вероятностью события А наз. относительная частота появления этого события в произведенных испытаниях.
29. Закон больших чисел (ЗБЧ) Свойства устойчивости массовых случайных явлений известно человечеству с древности. Суть сводится к следующему: конкретные особенности каждого отдельного случайного явления почти не сказываются на среднем результате массы таких явлений; случайные отклонения от среднего неизбежные в каждом отдельном явлении в массе взаимно погашаются, выравниваются. Эта устойчивость средних и предст. соб. содержание ЗБЧ. В широком смысле, при очень большом числе случайных явлений средний их результат практически перестает быть случайным и м б предсказан с большой степенью определенности. В узком смысле, это ряд математических теорем, каждая из кот. для тех или иных условий устанавливается как приближение средних характеристик большого числа опытов к некоторым определенным постоянным. Таким образом, закон больших чисел – это совокупность теорем, в которых приведены условия, при которых последовательность случайных величин подчиняется определенным закономерностям, то есть стремится к величине неслучайной.
31. Генеральная и выборочная совокупности. Вся подлежащая изучению совокупность объектов наблюдений называют генеральной совокупностью. Иными словами, совокупность всех возможных, всех мыслимых, значений исследуемой случайной величины. Понятие генеральной совокупности аналогично понятию случайной величины (закону распределения, вероятностному пространству). Та
часть объектов, которая отобрана для
непосредственного изучения из
генеральной совокупности, называется
выборочной
совокупностью или выборкой.
Число объектов в генеральной или в
выборочной совокупности называют их
объемом
4.
Наиболее распространенной в настоящее
время является логическая схема
построения основ теории вероятностей,
которая была разработана А.Н.Колмогоровым
в 1933 году. Основные
черты этой схемы следующие: при
изучении какой-либо задачи методами
теории вероятностей, прежде всего,
выделяется множество
Вероятность
события
Эти условия составляют аксиомы теории вероятностей. Геометрическая
вероятность события А
– отношение меры области благоприятствующих
появлению события к мере всей области,
т.е.
7. Следствием двух основных теорем вероятностей – теоремы сложения и теоремы умножения – являются формула полной вероятности и формула Байеса. Теорема:
если событие
А может произойти только при условии
появления одного из событий-гипотез
Н1,
Н2,
…, Нn,
образующих полную группу, то вероятность
события А равна сумме произведений
вероятностей каждого из этих событий
на соответствующие условные вероятности:
P(A)= Условная
вероятность гипотезы
Значение формулы Байеса состоит в том, что по мере получения новой информации, можно проверять и корректировать выдвинутые до испытания гипотезы. Такой подход, называемый байесовским, дает возможность корректировать управленческие решения в экономике, оценки неизвестных параметров распределения изучаемых признаков в статистическом анализе и т.п.
9.
Число
наступлений события
Определение: число m0 наступления события А в n независимых испытаниях называется наивероятнейшим, если вероятность осуществления этого события по крайней мере не меньше вероятности других событий при любом m. Теорема.
Наивероятнейшее
число наступлений события
20.
Определение:
Дискретная случайная величина Х имеет
биноминальный
закон распределения,
если она принимает значения 0,1,2…, m,…,
n
с вероятностями P(X=m)= Теорема.
Математическое
ожидание числа появлений события
Теорема.
Дисперсия
числа появлений события
18. Математическое ожидание характеризует среднее ожидаемое значение случайной величины, т.е. приближенно равно ее среднему значению (вероятностный смысл математического ожидания). Математическое ожидание характеризует положение случайной величины на числовой оси и принимается за среднее значение, вокруг которых происходит разброс возможных значений случайной величины. При малом разбросе возможных значений случайной величины относительно ее математического ожидания можно им пренебречь и считать, что данная величина полностью характеризуется ее математическим ожиданием, т.е. она неслучайна. Если же математическое ожидание мало, а разброс велик, то пренебрежение им, т.е. неучет случайности данной величины, приведет к недопустимым ошибкам. Математическим
ожиданием для дискретной случайной
величины
X
называется сумма произведений всех
ее значений на соответствующие им
вероятности, определяется по данной
формуле:
Математическим ожиданием непрерывной случайной величины называется несобственный интеграл (абсолютно сходящийся), все возможные значения которого принадлежат всей числовой оси и определяется по формуле:
Свойства математического ожидания для дискретных и непрерывных случайных величин: 1. Математическое ожидание постоянной величины С равно постоянной величине, т.е. M(C) = C. 2. Постоянный множитель можно вынести за знак математического ожидания, т.е. M(CX)=CM(X). 3. Математическое ожидание суммы случайных величин равно сумме их математических ожиданий, т.е. M (x1+………..+xn)=M(x1)+………….+M(xn). 4. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий, т.е. M (x1….xn)=M(x1) ….M(xn).
19.
На практике
часто требуется оценить рассеяние
случайной величины вокруг ее среднего
значения. Использовать в качестве
такой характеристики отклонение
Теорема.
Для любой
случайной величины
Доказательство.
Действительно,
учитывая, что M(X)
– постоянная величина, имеем:
Такой
характеристикой степени рассеяния
случайной величины
Дисперсией
(рассеянием)
случайной величины
Дисперсия
для дискретной случайной величины:
Дисперсия
для непрерывной случайной величины:
Свойства дисперсии: 1) Дисперсия постоянной величины равна нулю, т.е. Д(С)=0. 2) Постоянный множитель можно вынести за знак дисперсии, возводя его в квадрат, т.е. Д(СХ)=С2Д(Х). 3) Дисперсия суммы независимых случайных величин есть сумма их дисперсий, т.е. Д(х1+…+xn)=Д(х1)+…+Д(хn).
25.
Вычислим по формуле:
Если
Если
Если
Правило
«3 сигм»:
если случайная величина распределена
нормально, то абсолютная величина ее
отклонения от математического ожидания
не превосходит утроенного среднего
квадратичного отклонения.
В этом и состоит сущность правила
«трех сигм»
или если
случайная величина Х имеет нормальный
закон распределения с параметрами
26.
Определение.
Ковариацией (или
корреляционным
моментом)
Ковариация
двух случайных величин характеризует
как степень
зависимости
случайных величин, так и их рассеяние
вокруг точки
1. ковариация двух независимых случайных величин равна 0. 2. ковариация двух случайных величин равна математическому ожиданию их произведения минус произведение их математических ожиданий. 3. ковариация двух случайных величин по абсолютной величине не превосходит произведения их средних квадратических отклонений. Ковариация, как уже отмечено, характеризует не только степень зависимости двух случайных величин, но и их разброс, рассеяние. Кроме того, она – величина размерная, ее размерность определяется произведением размерностей случайных величин. Это затрудняет использование ковариации для оценки степени зависимости для различных случайных величин. Этих недостатков лишен коэффициент корреляции. Определение.
Коэффициент корреляции двух
случайных величин называется отношение
их ковариации к произведению средних
квадратичсеких отклонений этих
величин:
Свойства коэффициента корреляции: 1.
Коэффициент корреляции принимает
значения на отрезке [-1;1], т.е. -1 2.
Если случайные величины независимы,
то коэффициент корреляции равен нулю
( Случайные величины называются некоррелированными, если их коэффициент корреляции равен 0. Таким образом, из независимости случайных величин следует их некоррелированность. Обратное утверждение, вообще говоря, неверно: из некоррелированности двух случайных величин еще не следует их независимость. 3. Если коэффициент корреляции двух случайных величин равен (по абсолютной величине) единице (или вообще отличен от нуля), то между этими случайными величинами существует линейная функциональная зависимость.
32.
Статистическим
распределением выборки называют
перечень вариант и соответствующих
им относительных частот (полигон,
кумулянта, гистограмма)Заметим, что
в теории вероятностей под распределением
понимают соответствие между возможными
значениями случайной величины и их
вероятностями, а в математической
статистике – соответствие между
наблюдаемыми вариантами и их частотами
или относительными частотами. Полигон,
как правило, служит для изображения
дискретного вариационного ряда (любые
его варианты отличаются один от другого
на постоянную величину) и представляет
собой ломаную, в которой концы отрезков
прямой имеют координаты (хi,
ni)
i=1,2,
…, m.
Гистограмма служит
только для изображения интервальных
вариационных рядов и представляет
собой ступенчатую фигуру из
прямоугольников с основаниями, равными
интервалам значений признака и
высотами, равными частотам (частостям)
ni
(wi)
интервалов.
Если соединить середины верхних
оснований прямоугольников отрезками
прямой, то можно получить полигон того
же распределения. Кумулятивная
кривая (кумулянта) –
кривая накопленных частот (частостей).
Для дискретного ряда кумулянта
представляет собой ломанную, соединяющую
точки ( Весьма важным является понятие эмпирической функции распределения. Эмпирической
функцией распределения
Свойства эмпирической функции распределения:
Эмпирическая функция распределения выборки служит для оценки теоретической функции распределения генеральной совокупности.
40. Критерий Пирсона Критерием согласия называют критерий проверки гипотезы о предполагаемом законе неизвестного распределения. Наиболее часто используемым является критерий согласия К.Пирсона («хи квадрат»). В качестве критерия проверки нулевой гипотезы примем случайную величину:
Для
того, чтобы при заданном уровне
значимости проверить нулевую гипотезу
H0:
генеральная совокупность распределена
нормально, необходимо сначала вычислить
теоретические частоты, а затем
наблюдаемое значение критерия
Доказано,
что при n®¥
закон распределения случайной величины
(А) стремится к закону распределения
|
8. Повторные независимые испытания. Формула Бернули. Если
вероятность наступления события А в
каждом испытании не меняется в
зависимости от исходов других, то
такие испытания наз. Независимыми
относительно события А. Если независимые
повторные испытания проводятся при
одном и том же комплексе условий, то
вероятность наступления соб А в каждом
испытании одна и та же. Последовательность
независимых испытаний получила
название схема Бернули. Теорема: Если
вер-ть наступления события А в каждом
испытании постоянна, то вероятность
Рn
(m)
того, что соб А наступит m
раз в n
независимых испытаниях равна Рn
(m)=
10. Теорема Пуассона. Простейший поток событий. Если
вер-ть мала, а кол-во испытаний большое,
то применяется приближенные формулы
для вычисления вероятности. γ mp
≤20. Теорема: Если вероятность Р
наступления события А в каждом испытании
стремится к нулю при неограниченном
увеличении числа n
испытаний, при чем произведение np→к
постоянному числу γ, то вероятность
р того, что соб А появится m
раз в n
независимом испытании удовлетворяет
предельному равенству:
20. Биноминальный закон распределения. Пусть имеются n испытаний Бернулли с вероятностью успеха р и вероятностью неуспеха q, p+q=1. Дискретная СВ Х – число успехов имеет распределение: Р
(х=m)=
21. З-н распределения Пуассона. ДСВ
Х имеет ЗР Пуассона, если она принимает
значение 0, 1, 2 и т. д. m
(бесконечное, но счетное кол-во
значений)с вероятностями: Р
(х=m)= Где
22. Равномерный з-н распределения (графики) Равномерным наз-ся распределение СВ, все значения кот. лежат на некотором отрезке от α до β, т. е. [α;β] и имеют постоянную плотность вероятности на этом отрезке Выражение
плотности распределения вероятностей
Функция равномерного распределения задается формулой:
Математическое ожидание, дисперсия и среднее квадратическое отклонение соответственно равны:
30. Задачи математической статистики. Основные понятия матем-й статистики. Предметом МС явл-ся изучение событий и случайных величин по результатам наблюдений. МС занимается разработкой методов сбора, описания и анализа экспериментальных данных, полученных в результате наблюдения массовых случайных явлений. Выделяют 3 этапа: 1) Сбор данных 2) обработка данных 3) статистические выводы, прогноз, решение. Задачи МС: 1. Определение з-на распределения СВ по статистическим данным. 2. Проверка правдоподобия гипотез. 3. Нахождение неизвестных параметров распределения. При решении задач вероятность случайного события положена в равной относительной частоте. Вероятность - есть относительная частота, а матем. ожидание СВ приблизительно равно выборочному среднему. Статистической совокупностью наз совок предметов или явлений объединенных каким-либо общим признаком. Результатом наблюдений над статистической совокупностью явл-ся статистические данные – сведения о том, какие значения принял в итоге наблюдений интересующий нас признак (СВ Х)
5.
Теорема.
Вероятность
суммы несовместных событий равна
сумме вероятностей этих событий:
Теорема. Сумма вероятностей событий, образующих полную группу, равна единице: P(A)+P(B)+…+P(K)=1. Теорема.
Сумма
вероятностей противоположных событий
равна единице: P(A)+P(
6. Определение: Условной вероятностью события B при условии, что событие А уже произошло, называется число, которое обозначается: P(B/A)=PA(B). Определение: Два события называют независимыми, если появление одного из них не влияет на вероятность появления другого события, в противном случае зависимыми. Теорема: вероятность произведения двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие наступило. P(AB)=P(A) P(B/A). Следствие:
вероятность
произведения n-зависимых
событий равна произведению вероятности
одного из них события на условную
вероятность всех остальных событий,
при чем вероятность каждого последующего
события выполняется в предположении,
что все предыдущие произошли:
P(A1A2…An)=P(A1)
Следствие: вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их произведения: P(A+B)=P(A)+P(B)-P(AB). Теорема: вероятность произведения двух независимых событий равна произведению вероятностей этих событий: P(AB)=P(A) P(B).
13. Как для дискретной величины, так и для непрерывной вводится понятие функции распределения. Пусть
Тогда
вероятность того, что
Функция
распределения принимает значения из
промежутка
Вероятность
того, что случайная величина примет
значение из полуинтервала
Функция
распределения – неубывающая функция,
т.е.
Если
Если
15. Случайная величина называется непрерывной, если она может принимать значения, сколь угодно мало отличающиеся друг от друга. Непрерывной случайной величиной называют такую случайную величину X, множество значений которой есть некоторый числовой интервал или если функция распределения непрерывна. Случайная величина Х называется непрерывной, если функция распределена непрерывна в любой точке и дифференцируема всюду, кроме, быть может, отдельных точек. Теорема: вероятность любого отдельно взятого значения непрерывной случайной величины равна нулю. Следствие: если Х – непрерывная случайная величина, то вероятность попадания случайной величины в интервал (a, b) не зависит от того, является ли этот интервал открытым или закрытым. Распределением непрерывной случайной величины называется совокупность вероятностей. P (a x b), для любых a,bR. Непрерывная
случайная величина.
В отличие от случая дискретной случайной
величины в данном случае
Если
вероятность события
Вероятность того, что непрерывная случайная величина X примет одно определенное значение, равна нулю. Имеет смысл рассматривать лишь вероятность попадания ее в некоторый интервал, пусть даже и сколь угодно малый. График функции распределения для дискретной случайной величины представляет собой ступенчатую разрывную функцию, а непрерывной –монотонно возрастающую непрерывную функцию. Определение:
плотностью
вероятности непрерывной случайной
величины называется производная ее
функции распределения:
Свойства: плотность
вероятности есть – неотрицательная
функция, т.е.
вероятность
попадания непрерывной случайной
величины в интервал
функция
распределения непрерывной случайной
величины может выражена через плотность
вероятности по формуле: F(x)= несобственный
интеграл в бесконечных пределах от
плотности вероятности непрерывной
случайной величины равен единице:
24.
Определение.
Непрерывная
случайная величина Х имеет нормальный
закон распределения (закон Гаусса) с
параметрами а и
Кривую нормального закона распределения называют нормальной или гауссовой кривой. Теорема.
Математическое
ожидание случайной величины Х,
распределенной по нормальному закону,
равно параметру а
этого закона, а ее дисперсия –
Закон
положен в связи с разработкой теории
ошибок наблюдения. НСВ Х с а=0
и
Свойства: 1) вероятность попадания случайной величины в интервал от х1 до х2 равна: Р(х1
Х
х2)=(Ф(t2)
– Ф(t1)),
где
2)
вероятность того, что отклонение
случайной величины Х, распределенной
по нормальному закону, от математического
ожидания не превысит величину
27.
Среди числовых характеристик случайных
величин особое значение имеют моменты:
начальные
и центральные. Начальным
моментом k-ого
порядка случайной величины Х является
математическое ожидание k-ой
степени этой величины, т.е.
Для
более подробного описания распределения
служат моменты высших порядков. Третий
центральный момент
Четвертый
центральный момент
28. Неравенство Чебышева. Неравенство применяется для любых случайных величин. Теорема.
Для любой случайной величины, имеющей
математическое ожидание и дисперсию,
справедливо неравенство Чебышева.
Пусть имеется некоторая случайная
величина Х с M(X) и D(X). Каково не было бы
положительное число
Неравенство Маркова. Теорема.
Если
случайная величина Х принимает только
неотрицательные значения и имеет
математическое ожидание, то для любого
положительного числа
38. Cтатистической называют гипотезу о виде неизвестного распределения или о параметрах известных распределений. Примеры статистических гипотез: генеральная совокупность распределена по закону Пуассона; дисперсии двух нормальных распределений равны между собой. Нулевой (основной) называют выдвинутую гипотезу Альтернативной (конкурирующей) называют гипотезу, которая противоречит нулевой. Простой называют гипотезу, содержащую только одно предположение. Сложной называют гипотезу, состоящую из конечного или бесконечного числа простых гипотез. В итоге статистической проверки гипотезы в двух случаях может быть принято неправильное решение, т.е. могут быть допущены ошибки двух родов. Ошибка
первого рода
состоит в
том, что будет отвергнута
правильная
гипотеза.
Ошибка
второго рода
состоит в
том, что будет принята
неправильная
гипотеза. Следует отметить, что
последствия ошибок могут оказаться
различными. Вероятность совершения
ошибки первого
рода называют
уровнем
значимости
и обозначают
33.
Сформулируем задачу оценки параметров
в общем виде. Пусть распределение
признака X
– генеральной совокупности – задается
функцией вероятностей
В качестве статистических оценок параметров генеральной совокупности желательно использовать оценки, удовлетворяющие одновременно требованиям несмещенности, состоятельности, эффективности. Однако достичь это удается не всегда.
29. Закон больших чисел (ЗБЧ) Свойства устойчивости массовых случайных явлений известно человечеству с древности. Суть сводится к следующему: конкретные особенности каждого отдельного случайного явления почти не сказываются на среднем результате массы таких явлений; случайные отклонения от среднего неизбежные в каждом отдельном явлении в массе взаимно погашаются, выравниваются. Эта устойчивость средних и предст. соб. содержание ЗБЧ. В широком смысле, при очень большом числе случайных явлений средний их результат практически перестает быть случайным и м б предсказан с большой степенью определенности. В узком смысле, это ряд математических теорем, каждая из кот. для тех или иных условий устанавливается как приближение средних характеристик большого числа опытов к некоторым определенным постоянным. Таким образом, закон больших чисел – это совокупность теорем, в которых приведены условия, при которых последовательность случайных величин подчиняется определенным закономерностям, то есть стремится к величине неслучайной.
|
23. Показательный з-н распределения Показательным наз. распределение вероятностей НСВ Х, кот. описывается плотностью распределения вероятности.
где
Функция распределения случайной величины, распределенной по показательному закону, имеет вид:
Математическое
ожидание
4. Аксиоматическое определение вероятности. Геометрическое определение вероятности. При данном способе пространство элементарных событий является бесконечным, но все элементарные события, входящие в это пространство, являются равновозможными. Если
отождествлять пространство элементарных
событий с некоторой замкнутой областью
пространства из
где
Это
длина ( если рассматривается пространство
площадь
(если рассматривается пространство
объем
( если рассматривается пространство
Аксиоматическое определение вероятностей. Пространством элементарных событий наз. Произвольные множества, а его элементы – элементарными событиями. Аксиомы: 1) Р (А) >=0 2) Вероятность суммы несовместных событий равна суме этих событий Р (А+В)= Р(А)+Р(В) 3) Вероятность достоверного события Р (Ω) равна единице. Р (Ω)=1 4)
Для любой убывающей последовательности
А1>А2>А3…Аn
справедливо равенство
28. Неравенство Маркова и Чебышева. Неравенство
Чебышева
применяется для любых СВ. Пусть имеется
СВ Х с матем. ожиданием М(Х) и дисперсией
Д(Х). Каково бы ни было «+» число τ «тао»
вероятность того, что величина Х
отклонится от своего матем. ожид-я не
меньше, чем на тао , ограничена сверху
величиной
Р
Р
Неравенство
Маркова:
Если СВ Х принимает только отрицательное
значение и имеет матем. ожид-е, то для
любого положительного числа тао верное
неравенство: Р(х Р(х 11.
Предположим,
что в условиях схемы Бернулли проводится
Интегральная
теорема Муавра-Лапласа: Если
вероятность p
наступления события А в каждом испытании
постоянна и отлична от 0 и 1, то вероятность
того, что число m
наступления события А в n
независимых испытаниях заключено в
пределах от а до b
(включительно), при достаточно большом
числе n
(или: вероятность того, что число m
появления события А в схеме Бернулли
находится в заданном промежутке от а
до b,
при большом числе испытаний n)
приблизительно равна: P(a
m
b)
Чем больше n, тем точнее эта формула. При выполнении условия npq20 интегральная формула, так же как и локальная, дает незначительную погрешность вычисления вероятностей. Функция Ф(x) табулирована. Свойства функции Ф(x): 1) Функция Ф(x) нечетная, т.е. Ф(–x)= – Ф(x); 2) Функция Ф(x) монотонно возрастающая, причем при x+ Ф(x)1 (практически можно сказать, что уже при x>4 Ф(x)1) .
12.
Лаплас получил
важную приближенную формулу для
вероятности
Теорема.
Пусть
Локальная
теорема Муавра-Лапласа: если
вероятность p
наступления события А в каждом испытании
постоянна и отлична от о и 1, то
вероятность Pn(m)
того, что событие А произойдет m
раз в n
независимых испытаниях при достаточно
большом числе n,
приближенно равна:
Чем
больше n,
тем точнее приближенная формула,
вычисления дают незначительную
погрешность, когда npq20.
Для упрощения расчетов, связанных с
применением формулы, составлена
таблица значений функции
Свойства
функции
1.
Функция
2.
Функция
14. Дискретная случайная величина – это случайная величина, обозначаемая X называется дискретной, если она принимает конечное, или бесконечное, но счетное значение. Законом
распределения случайной дискретной
величины
называется
совокупность пар чисел (
21.
Определение:
дискретная
случайная величина Х имеет закон
распределения Пуассона,
если она принимает значения 0,1,2, … ,
m,
… (бесконечное, но счетное множество
значений) с вероятностями P(X=m)= Теорема.
Математическое
ожидание и дисперсия
случайной величины, распределенной
по закону Пуассона, совпадают и равны
параметру
17.
Очень часто результат испытания
характеризуется не одной случайной
величиной, а некоторой системой
случайных величин X1,
X2,
…, Xn,
которую
называют также многомерной
(n-мерной)
случайной величиной или
случайным
вектором Х= (X1,
X2,
…, Xn).
Примеры
многомерных случайных величин: 1)
успеваемость выпускника вуза
характеризуется системой n
случайных величин X1,
X2,
…, Xn
– оценками по различным дисциплинам,
поставленным в приложении к диплому;
2) погода в данном месте в определенной
время суток может быть охарактеризована
системой случайных величин:
22.
Определение.
Непрерывная
случайная величина Х имеет равномерный
закон распределения на
отрезке [ Теорема.
Функция
распределения случайной величины Х,
распределенной по равномерному закону,
есть:
Ее
математическое
ожидание:
23.
Определение.
Непрерывная
случайная величина Х имеет показательный
(экспоненциальный) закон распределения
с параметром
распределения
Теорема. Функция распределения случайной величины Х, распределенной по показательному (экспоненциальному) закону имеет следующие вид:
Ее
математическое
ожидание:
Для случайной величины, распределенной по показательному закону, математическое ожидание равно среднему квадратическому отклонению.
29. Свойство устойчивости массовых случайных явлений известно человечеству с древности: конкретные особенности каждого конкретного случайного явления почти не сказываются на среднем результате массы таких явлений; случайное отклонение от среднего неизбежные в каждом отдельном явлении в массе взаимно погашаются, выравниваются – это устойчивость средних и представляет собой физическое содержание закона больших чисел. Под законом больших чисел в широком смысле понимается общий принцип, согласно которому, по формулировке А. Н. Колмогорова, совокупное действие большого числа случайных факторов приводит (при некоторых весьма общих условиях) к результату, почти не зависящему от случая. Другими словами, при большом числе случайных величин их средний результат перестает быть случайным и может быть предсказан с большой степенью определенности. Под законом больших чисел в узком смысле понимается ряд математических теорем, в каждой из которых для тех или иных условий устанавливается факт приближения средних характеристик большого числа испытаний к некоторым определенным постоянным.
30. Предметом математической статистики является изучение случайных событий и случайных величин по результатам наблюдений. Совокупность предметов или явлений, объединенных каким-либо общим признаком, называется статистической совокупностью. Результатом наблюдений над статистической совокупностью являются статистические данные – сведения о том, какие значения принял в итоге наблюдений интересующий нас признак (случайная величина X). Обработка статистических данных методами математической статистики приводит к установлению определенных закономерностей, присущих массовым явлениям. При этом точность статистических выводов повышается с ростом числа наблюдений. Статистические
данные, как правило, представляют
собой ряд значений
Первая задача математической статистики – указать способы сбора и группировки статистических данных, полученных в результате наблюдений или в результате специально поставленных экспериментов. Второй задачей математической статистики является разработка методов анализа статистических данных в зависимости от целей исследования. К этой задаче относятся: оценка неизвестной вероятности события; оценка неизвестной функции распределения; оценка параметров распределения, вид которого известен; оценка зависимости случайной величины от одной или нескольких случайных величин и т.п.; проверка статистических гипотез о виде неизвестного распределения или о величине параметров распределения, вид которого известен. В современной математической статистике есть много общего с наукой о принятии решений в условиях неопределенности, так как она разрабатывает способы определения числа необходимых испытаний до начала исследования (планирование эксперимента), в процессе исследования (последовательный анализ) и решает многие другие аналогичные задачи. Типичными задачами математической статистики являются: 1) определение закона распределения случайной величины по статистическим данным; 2) проверка правдоподобия гипотез; 3) нахождение неизвестных параметров распределения. При решении задач вероятность случайного события полагать примерно равной относительной частоте, а математическое ожидание случайной величины приблизительно равно выборочному среднему.
31. Генеральной совокупностью называют совокупность объектов, из которых производится выборка. Совокупность всех возможных наблюдений, проводимых в одинаковых условиях над некоторой случайной величиной называется генеральной совокупностью. Генеральная совокупность – это набор объектов о которых нужно получить информацию. Генеральная совокупность может содержать конечное или бесконечное число элементов. Выборочной совокупностью или случайной выборкой называют совокупность случайно отобранных объектов. Отобранные из генеральной совокупности объекты называются выборочной совокупностью или выборкой. Число N-элементов – объем генеральной совокупности, n-элементов – объем выборочной совокупности. При составлении выборки можно поступать двумя способами: после того как объект отобран и исследован, его можно возвратить или не возвращать в генеральную совокупность. В связи с этим выборки подразделяются на повторные (отобранный объект перед отбором следующего возвращается в генеральную совокупность) и бесповторные (отобранный объект в генеральную совокупность не возвращается). Для того чтобы по данным выборки можно было достаточно уверенно судить об интересующем признаке генеральной совокупности, необходимо, чтобы объекты выборки правильно его представляли. Выборка должна правильно представлять пропорции генеральной совокупности, т.е. выборка должна быть репрезентативной (представительной). Пример – изучение общественного мнения. В силу закона больших чисел можно утверждать, что выборка будет репрезентативной, если ее осуществить случайно: каждый объект выборки отобран случайно из генеральной совокупности, если все объекты имеют одинаковую вероятность попасть в выборку. Если объем выборки достаточно велик, а выборка составляет лишь незначительную часть совокупности, то различие между повторной и бесповторной выборкой стирается. На практике применяются различные способы отбора, которые можно подразделить на два вида: 1) Отбор, не требующий расчленения генеральной совокупности на части. Сюда относятся а) простой случайный бесповторный отбор и б) простой случайный повторный отбор; 2) Отбор, при котором генеральная совокупность разбивается на части. Сюда относятся а) типический отбор, б) механический отбор и в) серийный отбор. Простым случайным называют отбор, при котором объекты извлекаются по одному из генеральной совокупности. Типическим называют отбор, при котором объекты отбираются не из всей генеральной совокупности, а из каждой ее “типической” части. Механическим называют отбор, при котором генеральная совокупность механически делится на столько групп, сколько объектов должно войти в выборку, а из каждой группы выбирается один объект. Серийным называют отбор, при котором объекты отбирают из генеральной совокупности не по одному, а “сериями”, которые подвергаются сплошному обследованию. На практике часто применяют комбинированный отбор, при котором сочетаются указанные выше способы.
|
||||||||||||

 таких,
что
таких,
что
 при
при

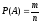 ,
, -
число элементарных исходов испытания,
благоприятствующих появлению события
-
число элементарных исходов испытания,
благоприятствующих появлению события
 ;
; -
общее число возможных элементарных
исходов испытания.
-
общее число возможных элементарных
исходов испытания. .
.
 .
. при условии того, что событие А
произошло, определяется по формуле
вероятности
гипотез
или формуле
Байеса (она
позволяет пересмотреть вероятность
гипотез после пересмотрения вероятности
события А) и определяется по формуле:
P(Hi/A)=
при условии того, что событие А
произошло, определяется по формуле
вероятности
гипотез
или формуле
Байеса (она
позволяет пересмотреть вероятность
гипотез после пересмотрения вероятности
события А) и определяется по формуле:
P(Hi/A)=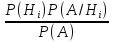 .
.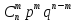 ,
где 0<p<1,
q=1
– p,
m=0,1,…,n.
Следовательно биноминальный
закон распределения
представляет собой закон распределения
X=m
наступления события А в n
независимых испытаниях, в каждом из
которых оно может произойти с одной
и той же вероятностью p.
,
где 0<p<1,
q=1
– p,
m=0,1,…,n.
Следовательно биноминальный
закон распределения
представляет собой закон распределения
X=m
наступления события А в n
независимых испытаниях, в каждом из
которых оно может произойти с одной
и той же вероятностью p.

 .
.
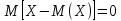
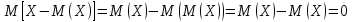
 –
определение
или
–
определение
или
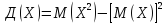 – для практических расчетов.
– для практических расчетов.
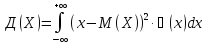 или
или
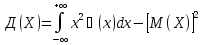 .
. при различных
значениях
при различных
значениях
 .
.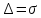 ,
то
,
то
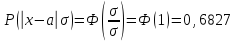
 ,
то
,
то
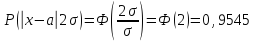
 ,
то
,
то

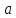
 ,
то практически достоверно, что ее
значения заключены в интервале (
,
то практически достоверно, что ее
значения заключены в интервале (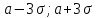 ).
). случайных величин Х и Y
называется математическое ожидание
произведения отклонений этих величин
от своих математических ожиданий,
т.е.
случайных величин Х и Y
называется математическое ожидание
произведения отклонений этих величин
от своих математических ожиданий,
т.е.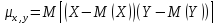 или
или
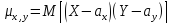 ,
где
,
где
 –
–
 ,
,
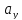 –
–
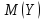 .
. .
Об этом, в частности, свидетельствуют
свойства
ковариации
случайных величин:
.
Об этом, в частности, свидетельствуют
свойства
ковариации
случайных величин: .
. 1.
1. ).
).
 )
или (
)
или ( )
i=1,2,
…, m.
Для интервального вариационного ряда
ломанная начинается с точки, абсцисса
которой равна началу первого интервала,
а ордината – накопленной частоте
(частости), равной нулю. Другие точки
этой ломанной соответствуют концам
интервалов.
)
i=1,2,
…, m.
Для интервального вариационного ряда
ломанная начинается с точки, абсцисса
которой равна началу первого интервала,
а ордината – накопленной частоте
(частости), равной нулю. Другие точки
этой ломанной соответствуют концам
интервалов.
 называется
относительная частота (частость) того,
что признак (случайная величина Х)
примет значение, меньшее заданного
х, т.е.
называется
относительная частота (частость) того,
что признак (случайная величина Х)
примет значение, меньшее заданного
х, т.е.

 – неубывающая
функция
– неубывающая
функция =0
при x
x1,
если
=0
при x
x1,
если
 -
наибольшая варианта, то
-
наибольшая варианта, то
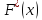 =1
при x
>
=1
при x
>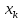 .
.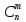 *
* *
* где
q=1-p
где
q=1-p
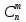 *
* *
*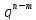 ,
где 0<р<1; q=1-р;
следовательно, , биноминальный ЗР
предст. соб. ЗР х=m
наступление соб А в n
независимых испытаниях, в каждом из
которых, оно может произойти с одной
и той же вероятностью р. Теорема:
Матем. ожид-е СВ Х, распределенное по
биноминальному з-ну ислис-ся по
формуле: М(х)=np;
D(х)=npq.
,
где 0<р<1; q=1-р;
следовательно, , биноминальный ЗР
предст. соб. ЗР х=m
наступление соб А в n
независимых испытаниях, в каждом из
которых, оно может произойти с одной
и той же вероятностью р. Теорема:
Матем. ожид-е СВ Х, распределенное по
биноминальному з-ну ислис-ся по
формуле: М(х)=np;
D(х)=npq.
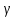 =np.
Теорема: Матем. ожид-е и Д (х) СВ,
распределенное по з-ну Пуассона
совпадают и равны параметру лямбда.
=np.
Теорема: Матем. ожид-е и Д (х) СВ,
распределенное по з-ну Пуассона
совпадают и равны параметру лямбда.
 имеет
следующий вид:
имеет
следующий вид:
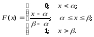


 .
. =1.
=1.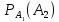
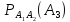 …….
……. пробегает все непрерывное множество
значений, а сама функция
пробегает все непрерывное множество
значений, а сама функция
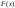 возрастает монотонно.
возрастает монотонно.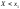 равна
равна
 ,
а вероятность события
,
а вероятность события
 равна
равна
 ,
то вероятность того, что случайная
величина
,
то вероятность того, что случайная
величина
 заключена между
заключена между
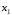 и
и
 равна разности соответствующих
значений функции распределения:
равна разности соответствующих
значений функции распределения:
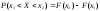 .
. .
.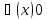 ;
; равна определенному интегралу от ее
плотности вероятности в пределах от
а до b,
т.е. P
(a
X
b)
=
равна определенному интегралу от ее
плотности вероятности в пределах от
а до b,
т.е. P
(a
X
b)
=
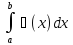 ,
геометрически это площадь криволинейной
трапеции;
,
геометрически это площадь криволинейной
трапеции; ;
; .
. ,
если ее плотность вероятности имеет
вид:
,
если ее плотность вероятности имеет
вид:
 ,
где а –
математическое ожидание,
,
где а –
математическое ожидание,
 – дисперсия.
– дисперсия.

 =1
называется стандартной нормальной
величиной. Распределение вероятностей
нормальной случайной величины является
нормальным распределением. Общим
называется
нормальное распределение с произвольными
параметрами а
и
=1
называется стандартной нормальной
величиной. Распределение вероятностей
нормальной случайной величины является
нормальным распределением. Общим
называется
нормальное распределение с произвольными
параметрами а
и
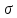 (
( ).
Плотность стандартного распределения
).
Плотность стандартного распределения (табулирована).
Функция
F(x)
общего нормального распределения
имеет вид:
(табулирована).
Функция
F(x)
общего нормального распределения
имеет вид:
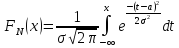 ,а
функция
стандартного нормального распределения:
,а
функция
стандартного нормального распределения: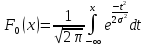 .
(табулированное
значение).
.
(табулированное
значение).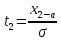 ,
,
 .
. (по абсолютной величине равна:
(по абсолютной величине равна:
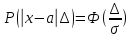 ).
).
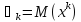 .
Центральным моментом k-ого
порядка случайной величины Х является
математическое ожидание k-ой
степени отклонения случайной величины
Х от ее математического ожидания, т.е.
.
Центральным моментом k-ого
порядка случайной величины Х является
математическое ожидание k-ой
степени отклонения случайной величины
Х от ее математического ожидания, т.е.
 .
.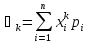



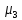 служит для характеристики асимметрии
(скошенности
распределения). Чтобы получить
безразмерную величину ее делят на
служит для характеристики асимметрии
(скошенности
распределения). Чтобы получить
безразмерную величину ее делят на
 ,
где
,
где
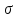 – среднее
квадратическое отклонения случайной
величины Х. Полученная величина А
называется коэффициентом
асимметрии случайной величины:
– среднее
квадратическое отклонения случайной
величины Х. Полученная величина А
называется коэффициентом
асимметрии случайной величины:
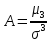 .
. служит для
характеристики крутости распределения.
Эксцессом
случайной величины называется число
Е:
служит для
характеристики крутости распределения.
Эксцессом
случайной величины называется число
Е:
 .
Если Е<0
– кривая более островершинная. Если
Е>0 – кривая более плосковершинная.
.
Если Е<0
– кривая более островершинная. Если
Е>0 – кривая более плосковершинная.
 , вероятность того, что величина Х
отклонится от своего математического
ожидания не меньше чем на
, вероятность того, что величина Х
отклонится от своего математического
ожидания не меньше чем на
 ,
ограничена сверху величиной
,
ограничена сверху величиной
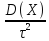 :
: ИЛИ
ИЛИ

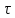 ,
верно неравенство, т.е. вероятность
того, что случайная величина Х примет
какое-нибудь значение превосходящее
положительное значение
,
верно неравенство, т.е. вероятность
того, что случайная величина Х примет
какое-нибудь значение превосходящее
положительное значение
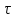 не больше дроби
не больше дроби
 :
: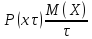 ИЛИ
ИЛИ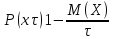
 .
Чаще всего уровень значимости принимают
равным 0,05 или 0,01. Если, например, принят
уровень значимости 0,05, то это означает,
что в пяти случаях из ста имеется риск
допустить ошибку первого рода
(отвергнуть правильную гипотезу).
.
Чаще всего уровень значимости принимают
равным 0,05 или 0,01. Если, например, принят
уровень значимости 0,05, то это означает,
что в пяти случаях из ста имеется риск
допустить ошибку первого рода
(отвергнуть правильную гипотезу).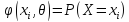 (для дискретной случайной величины
Х) или плотностью вероятности
(для дискретной случайной величины
Х) или плотностью вероятности
 (для непрерывной случайной величины
Х), которая содержит неизвестный
параметр
(для непрерывной случайной величины
Х), которая содержит неизвестный
параметр
 .Например,
это параметр
.Например,
это параметр
 в распределении Пуассона или параметры
a
и
в распределении Пуассона или параметры
a
и
 для нормального закона распределения
и т.д. Для вычисления параметра
для нормального закона распределения
и т.д. Для вычисления параметра
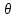 исследовать
все элементы генеральной совокупности
не представляет возможным. Поэтому о
параметре
исследовать
все элементы генеральной совокупности
не представляет возможным. Поэтому о
параметре
 пытаются
судить по выборке, состоящей из значений
x1,
x2,
…, xn.
Эти значения можно рассматривать как
частные значения (реализации) n
независимых случайных величин Х1,
Х2,
…, Хn,
каждая из которых имеет тот же закон
распределения, что и сама случайная
величина Х. Определение.
Оценкой
пытаются
судить по выборке, состоящей из значений
x1,
x2,
…, xn.
Эти значения можно рассматривать как
частные значения (реализации) n
независимых случайных величин Х1,
Х2,
…, Хn,
каждая из которых имеет тот же закон
распределения, что и сама случайная
величина Х. Определение.
Оценкой
 параметра
параметра
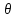 называют
всякую функцию результатов наблюдений
над случайной величиной Х (иначе –
статистику), с помощью которой судят
о значении параметра
называют
всякую функцию результатов наблюдений
над случайной величиной Х (иначе –
статистику), с помощью которой судят
о значении параметра
 :
:
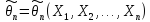 .
Поскольку
.
Поскольку
 - случайные
величины, то и оценка
- случайные
величины, то и оценка
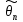 (в отличии от оцениваемого параметра
(в отличии от оцениваемого параметра
 – величины неслучайной, детерминированной)
является случайной величиной, зависящей
от закона распределения случайной
величины Х и числа n.
Определение.
Оценка
– величины неслучайной, детерминированной)
является случайной величиной, зависящей
от закона распределения случайной
величины Х и числа n.
Определение.
Оценка
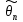 параметра
параметра
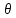 называется несмещенной,
если ее математическое ожидание равно
оцениваемому параметру, т.е.
называется несмещенной,
если ее математическое ожидание равно
оцениваемому параметру, т.е.
 .
В противном случае оценка называется
смещенной.
Требование несмещенности гарантирует
отсутствие систематических ошибок
при оценивании. Определение.
Оценка
.
В противном случае оценка называется
смещенной.
Требование несмещенности гарантирует
отсутствие систематических ошибок
при оценивании. Определение.
Оценка
 параметра
параметра
 называется состоятельной,
если она удовлетворяет закону больших
чисел, т.е. сходится по вероятности к
оцениваемому параметру:
называется состоятельной,
если она удовлетворяет закону больших
чисел, т.е. сходится по вероятности к
оцениваемому параметру:
 .
Состоятельной
называется статистическая оценка,
которая при n
стремится по вероятности к оцениваемому
параметру. Например, если дисперсия
несмещенной оценки при n
стремится к нулю, то такая оценка
оказывается и состоятельной. В случае
использования состоятельных оценок
оправдывается увеличение объема
выборки, так как при этом становятся
маловероятными значительные ошибки
при оценивании. Поэтому практический
смысл имеют только состоятельные
оценки.
Определение.
Несмещенная
оценка
.
Состоятельной
называется статистическая оценка,
которая при n
стремится по вероятности к оцениваемому
параметру. Например, если дисперсия
несмещенной оценки при n
стремится к нулю, то такая оценка
оказывается и состоятельной. В случае
использования состоятельных оценок
оправдывается увеличение объема
выборки, так как при этом становятся
маловероятными значительные ошибки
при оценивании. Поэтому практический
смысл имеют только состоятельные
оценки.
Определение.
Несмещенная
оценка
 параметра
параметра
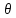 называется эффективной,
если она
имеет наименьшую дисперсию среди всех
возможных несмещенных оценок параметра
называется эффективной,
если она
имеет наименьшую дисперсию среди всех
возможных несмещенных оценок параметра
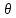 ,
вычисленных по выборкам одного и того
же объема n.
Эффективной
называют статистическую оценку,
которая, при заданном объеме выборки
n,
имеет наименьшую возможную дисперсию.
Эффективность
оценки
,
вычисленных по выборкам одного и того
же объема n.
Эффективной
называют статистическую оценку,
которая, при заданном объеме выборки
n,
имеет наименьшую возможную дисперсию.
Эффективность
оценки
 определяется отношением дисперсии
эффективной и данной оценок:
определяется отношением дисперсии
эффективной и данной оценок:
 , чем ближе e
к 1, тем эффективнее оценка. Если e1,
n,
то такая оценка называется асимптотически
эффективной.
, чем ближе e
к 1, тем эффективнее оценка. Если e1,
n,
то такая оценка называется асимптотически
эффективной.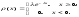
 постоянная и называется параметром
экспоненциального распределения.
постоянная и называется параметром
экспоненциального распределения.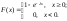
 .
Дисперсия
.
Дисперсия
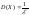 ,
среднее квадратическое отклонение
,
среднее квадратическое отклонение
 .
.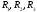 ,
то вероятность события
,
то вероятность события
 будет вычисляться по формуле
будет вычисляться по формуле
 и
и
 мера
области :
мера
области :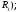


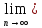 Р(Аn)=0
Р(Аn)=0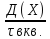 ,
где τ2
любое «+» число.
,
где τ2
любое «+» число.
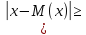 τ
τ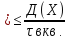 ,
или
,
или
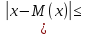 τ
τ
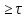 )
) ;
;
 )
)
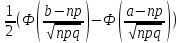 ,
где Ф(x)=
,
где Ф(x)=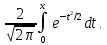
 ,
где
,
где
 ;
;
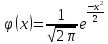
 .
.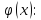
 четной, т.е.
четной, т.е.
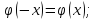
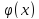 – монотонно
убывающая при положительных значениях
x,
причем при x
– монотонно
убывающая при положительных значениях
x,
причем при x
 0
(практически можно считать, что уже
при x>4
0
(практически можно считать, что уже
при x>4
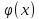 0)
.
0)
. . Простейшей формой задания закона
распределения дискретной случайной
величины является таблица, в которой
перечислены возможные значения
случайной величины и соответствующие
им вероятности, причем сумма вероятностей
должна быть равна 1. Таблица называется
рядом
распределения.
Для наглядности изображается графически,
отмечая точки, строя прямоугольник
распределения.
. Простейшей формой задания закона
распределения дискретной случайной
величины является таблица, в которой
перечислены возможные значения
случайной величины и соответствующие
им вероятности, причем сумма вероятностей
должна быть равна 1. Таблица называется
рядом
распределения.
Для наглядности изображается графически,
отмечая точки, строя прямоугольник
распределения.
 ,
где m=0,1,2,
…;
,
где m=0,1,2,
…;
 .
. этого закона, т.е. М(Х)=
этого закона, т.е. М(Х)= ,
Д(Х)=
,
Д(Х)= .
. – температура,
– температура,
 – влажность,
– влажность,
 – давление,
– давление,
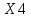 – скорость ветра и т.п. В
теоретико-множественной трактовке
любая случайная величина
– скорость ветра и т.п. В
теоретико-множественной трактовке
любая случайная величина
 есть
функция элементарных событий
есть
функция элементарных событий
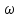 ,
входящих в пространство элементарных
событий
,
входящих в пространство элементарных
событий
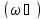 .
Поэтому и многомерная
случайная
величина есть функция элементарных
событий
.
Поэтому и многомерная
случайная
величина есть функция элементарных
событий
 :
(X1,
X2,
…, Xn)=
:
(X1,
X2,
…, Xn)= т.е.
каждому элементарному событию
т.е.
каждому элементарному событию
 ставится в соответствие несколько
действительных чисел х1,
х2,
…, хn,
которые приняли случайные величины
X1,
X2,
…, Xn
в результате испытания. В этом случае
вектор х=
(х1,
х2,
…, хn)
называется реализацией
случайного вектора Х= (X1,
X2,
…, Xn).
Случайные
величины X1,
X2,
…, Xn,
входящие
в систему, могут быть как дискретными,
так и
непрерывными.
Наиболее
полным, исчерпывающим описанием
многомерной случайной величины
является закон
ее распределения.
При конечном множестве возможных
значений многомерной случайной
величины такой закон может быть задан
в форме таблицы (матрицы), содержащей
всевозможные сочетания значений
каждой из одномерных случайных величин,
входящих в систему, и соответствующие
им вероятности. Так, если рассматривается
двумерная
дискретная случайная величина (X,
Y),
то ее двумерное распределение можно
представить в виде таблицы
(матрицы) распределения,
в каждой клетке (i,
j)
которой располагаются вероятности
произведения событий pij=
P[(X=xi)
(Y=yj)].
ставится в соответствие несколько
действительных чисел х1,
х2,
…, хn,
которые приняли случайные величины
X1,
X2,
…, Xn
в результате испытания. В этом случае
вектор х=
(х1,
х2,
…, хn)
называется реализацией
случайного вектора Х= (X1,
X2,
…, Xn).
Случайные
величины X1,
X2,
…, Xn,
входящие
в систему, могут быть как дискретными,
так и
непрерывными.
Наиболее
полным, исчерпывающим описанием
многомерной случайной величины
является закон
ее распределения.
При конечном множестве возможных
значений многомерной случайной
величины такой закон может быть задан
в форме таблицы (матрицы), содержащей
всевозможные сочетания значений
каждой из одномерных случайных величин,
входящих в систему, и соответствующие
им вероятности. Так, если рассматривается
двумерная
дискретная случайная величина (X,
Y),
то ее двумерное распределение можно
представить в виде таблицы
(матрицы) распределения,
в каждой клетке (i,
j)
которой располагаются вероятности
произведения событий pij=
P[(X=xi)
(Y=yj)].
 ],
если ее плотность
],
если ее плотность
 (х)
постоянна на этом отрезке и равна нулю
вне его, т.е.:
(х)
постоянна на этом отрезке и равна нулю
вне его, т.е.:
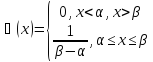
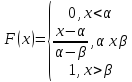
 ,
а дисперсия:
,
а дисперсия:
 .
. ,
если плотность вероятности имеет вид:
,
если плотность вероятности имеет вид:

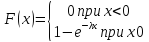
 ,
а дисперсия:
,
а дисперсия:
 .
.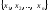 некоторой случайной величины. Обработка
этого ряда значений представляет
собой первый этап исследования
случайной величины.
некоторой случайной величины. Обработка
этого ряда значений представляет
собой первый этап исследования
случайной величины.