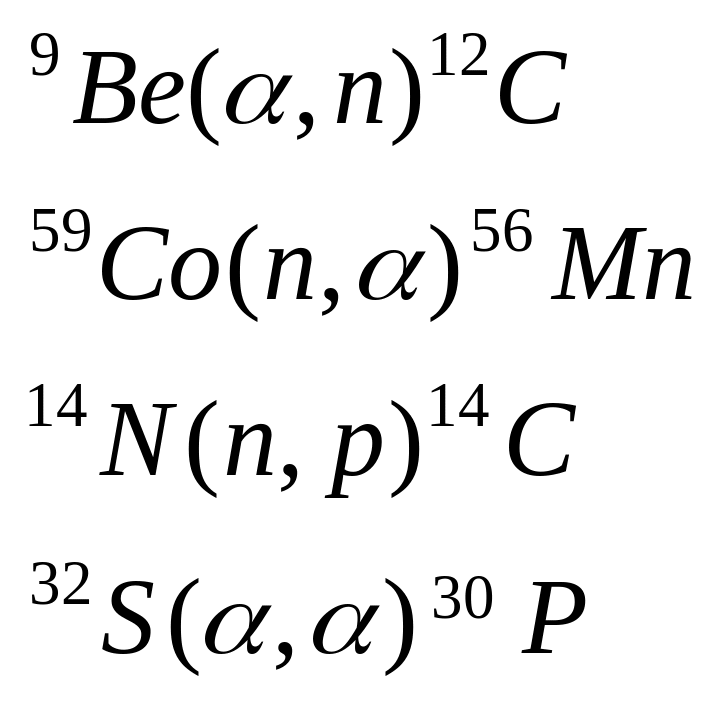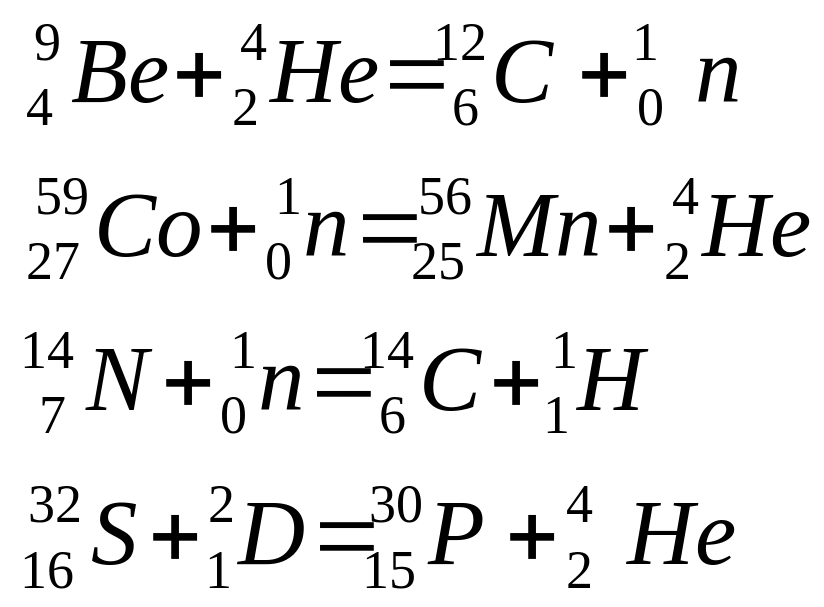- •Продовження таблиці 1
- •Контрольні питання
- •1.2 Будова атома
- •Контрольні питання
- •Контрольні питання
- •1.4 Хімічна спорідненість
- •Контрольні питання
- •Чи є можливою ця реакція при стандартних умовах?
- •1.5 Хімічна кінетика і рівновага
- •Контрольні питання
- •1 Окислення сірки і її діоксиду протікає за рівняннями:
- •1.6 Способи вираження концентрації розчину
- •Контрольні питання
- •1.7 Іонно-молекулярні (іонні) реакції обміну
- •Контрольні питання
- •1.8 Гідроліз солей
- •Контрольні питання
- •Контрольне завдання № 2
- •2.1 Окисно-відновні реакції
- •Контрольні питання
- •2.2 Електродні потенціали та електрорушійні сили
- •Контрольні питання
- •2.3 Електроліз
- •Контрольні питання
- •2.4 Корозія металів
- •Контрольні питання
- •2.5 Твердість води і методи її усунення
- •Контрольні питання
- •2.6 Органічні сполуки. Полімери Контрольні питання
- •Список літератури
- •Додаток а
1.2 Будова атома
Приклад 1. Що таке квантові числа? Яких значень вони можуть набувати?
Розв’язання. Рух електрона в атомі носить імовірний характер. Навколоядерний простір, у якому з найбільшою ймовірністю (0,9—0,95) може знаходитись електрон, називається атомною орбіталлю (АО). Атомна орбіталь, як будь-яка геометрична фігура, характеризується трьома параметрами (координатами), що одержали назву квантових чисел (n, l, ml). Квантові числа набувають не будь-яких, а визначених, дискретних значень. Сусідні значення квантових чисел розрізняються на одиницю. Квантові числа визначають розмір (n) , форму (l) та орієнтацію (ml) атомної орбіталі у просторі. Займаючи атомну орбіталь, електрон утворює електронну оболонку, яка у електронів одного і того ж атома може мати різну форму (рисунок 1). Форми електронних оболонок аналогічні атомним орбіталям. Електронна оболонка характеризується чотирма квантовими числами (n, l, ml, ms).


Рисунок 1 – Форми s-, р- і d-електронних хмар (орбіталей)
Ці квантові числа пов’язані з фізичними властивостями електрона і, число n (головне квантове число) характеризує енергетичний (квантовий) рівень електрона; число l (орбітальне) – момент кількості руху (енергетичний підрівень), число ml (магнітне) – магнітний момент, ms - спін. Спін електрона виникає при його обертанні навколо власної осі. Електрони в атомі повинні відрізнятися хоч би одним квантовим числом (принцип Паулі), тому що в АО може знаходитись не більше двох електронів , які відрізняються спінами (ms=±1/2). В таблиці 3 дані значення та визначення квантових чисел, а також кількість електронів на відповідному енергетичному рівні та підрівні.
Таблиця 3 – Значення квантових чисел і максимальне число електронів на квантових рівнях і підрівнях
Квантовий |
Магнітне квантове число ml |
Число квантових орбіталей |
Максимальна кількість електронів |
|||||
Рівень |
Підрівень |
У підрівні (2l+1) |
У рівні n2 |
У підрівні 2(2l+1) |
У рівні 2n2 |
|||
Поз-начення |
Головне кван-тове число n |
Поз-начення |
Орбітальне квантове число l |
|||||
K |
1 |
S |
0 |
0 |
1 |
1 |
2 |
2
|
|
2 |
S P |
0 1 |
0 -1,0+1 |
1 3 |
4 |
2 6 |
8 |
|
3 |
S P D |
0 1 2 |
0 -1,0,+1 -2,-1,0,+1,+2 |
1 3 5 |
9
|
2 6 10 |
18 |
|
4 |
S P D F |
0 1 2 3 |
0 -1,0,+1 -2,-1,0,+1,+2 -3, -2, -1, 0, +1, +2, +3 |
1 3 5 7 |
16 |
2 6 10 14 |
32 |
Приклад 2. Складіть електронні формули атомів елементів із порядковими номерами 16 і 22. Покажіть розподіл електронів по орбіталях.
Розв’язання. Електронні формули відображають розподіл електронів в атомі за енергетичними рівнями, підрівнями (атомними орбіталями) . Електронна конфігурація позначається групами символів nlx, де n — головне квантове число, l – орбітальне квантове число (замість нього указують відповідне позначення — s, p, d, f) , х- кількість електронів у даному підрівні (орбіталі).
При цьому варто враховувати, що електрон займає той енергетичний підрівень, на якому він має найменшу енергію – менша сума n+ l (правило Клечковського). Послідовність заповнення енергетичних рівнів і підрівнів така:
1s2s2p3s3p4s3d4p5s4d5p6s(5d1)4f5d6p 7s (6d1-2) 5f6d7p.
Через те що число електронів в атомі того чи іншого елемента дорівнює його порядковому номеру в таблиці Д. І. Менделєєва, то для елементів № 16 (сірка) і № 22 (титан) електронні формули мають вигляд
16S 1s22s22p63s23p4
22 Тi 1s22s22p63s23p63d24s2.
Е лектронна
структура атома може бути зображена
також у вигляді схем розміщення електронів
у квантових (енергетичних) ячейках, які
є схематичним зображенням атомних
орбіталей (АО). Квантову ячейку позначають
у вигляді прямокутника , а електрони
в цих ячейках позначають стрілками. У
кожній квантовій ячейці може бути не
більш двох електронів із протилежними
спінами
лектронна
структура атома може бути зображена
також у вигляді схем розміщення електронів
у квантових (енергетичних) ячейках, які
є схематичним зображенням атомних
орбіталей (АО). Квантову ячейку позначають
у вигляді прямокутника , а електрони
в цих ячейках позначають стрілками. У
кожній квантовій ячейці може бути не
більш двох електронів із протилежними
спінами
![]() .
.
Орбіталі даного підрівня заповнюються спочатку по одному електрону з однаковими спінами, а потім по другому електрону з протилежними спінами (правило Хунда):
↑↓ |
|
|||||||||
↑↓ |
↑↓ |
↑↓ |
↑↓ |
|
||||||
↑↓ |
↑↓ |
↑ |
↑ |
|
|
|
|
|
||
Приклад 3
Ізотоп 101-го елемента – менделєєвію (256) одержали бомбардуванням α – частками ядер атомів ейнштейнію (253). Скласти рівняння ядерної реакції.
Розв’язання.
Перетворення атомних ядер обумовлено
взаємодією з елементарними частками
та між собою. Ядерні реакції, пов’язані
із зміною складу ядер атомів хімічних
елементів. За допомогою ядерних реакцій
можливо з атомів одного елемента одержати
атоми іншого . Перетворення атомних
ядер як при природній, так і при штучній
радіоактивності записують у вигляді
рівнянь ядерних реакцій. При цьому варто
пам'ятати, що суми масових чисел (цифри,
що знаходяться біля символу елемента
вгорі ліворуч) і алгебраїчні суми зарядів
(цифри, що знаходяться біля символу
елемента внизу ліворуч) часток у лівій
і правій частинах рівності повинні бути
рівні. Дану ядерну реакцію виражають
рівнянням
![]() .
.
Часто
застосовують скорочену форму запису.
Для приведеної реакції вона має вигляд:
253Es(α,
n)256
Md. У дужках на першому місці пишуть
частку, що бомбардує, а на другому, через
кому, — частку, що утвориться при даному
процесі. У скорочених рівняннях частки
![]() He;
He;
![]() H;
H;
![]() D;
D;
![]() n
позначають відповідно α, р, d, n.
n
позначають відповідно α, р, d, n.
Приклад 4. Виходячи зі скорочених рівнянь ядерних реакцій (таблиця 2), напишіть їхні повні рівняння.
Розв’язання. Відповідь на питання у таблиці 4.
Таблиця 4 –Скорочені й повні рівняння ядерних реакцій
Скорочені рівняння |
Повні рівняння |
|
|

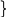 L
L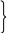 M
M N
N