
- •Красноярский государственный технический университет Радиотехнический факультет Теория телетрафика
- •Цели и задачи дисциплины.
- •Требования к уровню освоения содержания дисциплины.
- •Содержание дисциплины.
- •Контрольные вопросы.
- •Контрольные задания.
- •6. Указания к выполнению заданий.
- •7. Литература.
- •8. Справочные материалы.
6. Указания к выполнению заданий.
Задание 1.
Для выполнения данной задачи необходимо изучить характеристики математических моделей примитивного и простейшего потоков вызовов; определить смысл понятий, определяющих качество обслуживания вызовов; конкретизировать параметры качества обслуживания по отношению к обслуживанию полнодоступным пучком простейшего и примитивного потоков вызовов.
Вероятность
занятия
![]() линий полнодоступного пучка при
обслуживании простейшего потока:
линий полнодоступного пучка при
обслуживании простейшего потока:
 ,
где
,
где
![]() -
интенсивность поступающей нагрузки;
-
интенсивность поступающей нагрузки;
![]() - первая формула Эрланга.
- первая формула Эрланга.
Вероятность
потерь по времени при обслуживании
простейшего потока полнодоступным
пучком:
 ,
вероятность потерь по нагрузке:
,
вероятность потерь по нагрузке:
![]() ,
вероятность потерь по вызовам:
,
вероятность потерь по вызовам:
![]() .
.
При обслуживании примитивного потока вызовов полнодоступным пучком вероятность занятия линий определяется формулой Энгсета:
 ,
где
,
где
![]() - удельная нагрузка от одного источника,
- удельная нагрузка от одного источника,
![]() - число сочетаний
из
- число сочетаний
из
![]() .
.
Вероятность
потерь по времени при обслуживании
примитивного потока полнодоступным
пучком:
![]() ;
по нагрузке:
;
по нагрузке:
![]() ;
по вызовам:
;
по вызовам:
![]() .
.
Задание 2.
В системе массового обслуживания вида M/M/s имеется s каналов обслуживания и бесконечное число мест ожидания. Вероятность нахождения в системе i требований определяется следующим распределением:

В связи с тем, что при отсутствии свободных линий поступающий вызов поступает на ожидание обслуживания, то возникают потери по времени, которые определяются как (вторая формула Эрланга):
 .
.
Распределение
времени ожидания подчиняется следующему
закону:
![]() .
Откуда, среднее время ожидания начала
обслуживания определяется, как:
.
Откуда, среднее время ожидания начала
обслуживания определяется, как:
![]() ,
а средняя очередь в системе обслуживания
будет равна:
,
а средняя очередь в системе обслуживания
будет равна:
![]() .
.
Задание 3.
При решении этой задачи необходимо знать понятия нагрузки, интенсивности нагрузки, концентрации нагрузки, основные параметры нагрузки и использование всех данных понятий при расчете средней и расчетной интенсивностей нагрузки.
Нагрузка,
поступающая на АТС от
![]() категорий источников равна:
категорий источников равна:
![]() ,
где
- число источников данной категории;
,
где
- число источников данной категории;
![]() - среднее число вызовов от одного
источника этой категории;
- среднее число вызовов от одного
источника этой категории;
![]() - среднее время обслуживания одного
источника данной категории.
- среднее время обслуживания одного
источника данной категории.
Среднее время обслуживания определяется различными способами:
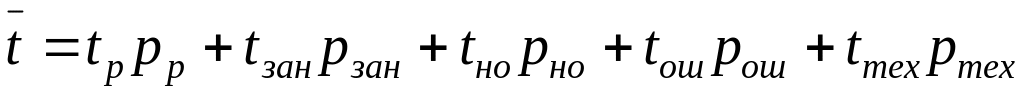 ,
где переменные с индексом «р» относятся
к вызову закончившемуся разговором;
все остальные переменные связаны с
непроизводительным занятием приборов
АТС: индекс «зан» – вызов при занятости
абонента; «но» – неответ вызываемого
абонента; «ош» – ошибка в наборе номера;
«тех» – техническая ошибка на АТС.
,
где переменные с индексом «р» относятся
к вызову закончившемуся разговором;
все остальные переменные связаны с
непроизводительным занятием приборов
АТС: индекс «зан» – вызов при занятости
абонента; «но» – неответ вызываемого
абонента; «ош» – ошибка в наборе номера;
«тех» – техническая ошибка на АТС. ,
где
,
где
 - время посылки вызова;
- время посылки вызова;
 - среднее время разговора;
- среднее время разговора;
 -
время слушания сигнала ответа станции;
-
время слушания сигнала ответа станции;
 - время установления соединения; а 4.5 с
учитывают непроизводительную нагрузку
на АТС.
- время установления соединения; а 4.5 с
учитывают непроизводительную нагрузку
на АТС.
Значения длительности составляющих среднего времени обслуживания, не приведенные в таблице исходных данных и в таблице 6 справочных данных, студент выбирает исходя из собственных соображений. Это же относится и к вероятностным характеристикам.
Расчетное
значение поступающей нагрузки определяется
по формуле:
![]() .
.
Задание 4.
Сущность метода О’Делла заключается в выборе из всех возможных решений системы:

такого,
которое минимизирует выражение
![]() ,
,
где
![]() -
число шагов искания, в которых каждая
линия объединяет по
выходов (
-
число шагов искания, в которых каждая
линия объединяет по
выходов (![]() ).
).
При
решении задачи методом оптимизирующих
коэффициентов, необходимо: используя
таблицу оптимизирующих коэффициентов
для построения оптимальных неполнодоступных
схем (таблица 7), определить число линий
на каждом шаге искания:
![]() ,
далее округлить получившиеся значения
в соответствии с заданной структурой
схемы.
,
далее округлить получившиеся значения
в соответствии с заданной структурой
схемы.
Задача 4.
Метод
Якобеуса заключается в решении системы
уравнений (относительно
![]() и
и
![]() ):
):

где:
![]() -
нагрузка на один вход ступени;
-
нагрузка на один вход ступени;
-
нагрузка на полнодоступный пучок
емкостью
![]() при потерях р;
при потерях р;
-
удельная нагрузка на одну из
![]() линий направления;
линий направления;
![]() -
емкость неполнодоступного пучка;
-
емкость неполнодоступного пучка;
![]() -
параметры ступени.
-
параметры ступени.
Метод
эффективной доступности основан на
замене двухзвенной блокирующейся схемы
однозвенной неполнодоступной схемой
с доступностью
![]() .
.
![]() ,
где:
,
где:
![]() -
минимальная доступность в направлении;
-
минимальная доступность в направлении;
![]() ;
;
![]() -
нагрузка пропускаемая
-
нагрузка пропускаемая
![]() промлиниями.
промлиниями.
Определив
![]() ,
по таблице 8 при заданных потерях
определяются коэффициенты для вычисления
числа линий.
,
по таблице 8 при заданных потерях
определяются коэффициенты для вычисления
числа линий.
Задача 5.
Межстанционная нагрузка рассчитывается как функция нормированных коэффициентов тяготения, величины которых в основном определяются расстоянием по прямой между станциями. На рис. 1 приведена графическая зависимость нормированных коэффициентов тяготения от расстояния, которым можно воспользоваться для определения последних.
После определения значений нормированных коэффициентов тяготения определяют межстанционную нагрузку по формуле:
 ,
где:
,
где:
![]() -
нагрузка от j-ой станции к i-ой;
-
нагрузка от j-ой станции к i-ой;
![]() -
коэффициент тяготения от j-ой станции
к i-ой;
-
коэффициент тяготения от j-ой станции
к i-ой;
![]() -
нагрузка на выходе ступени ГИ (86% от
-
нагрузка на выходе ступени ГИ (86% от
![]() ).
).
