Лекция 2. Последовательности.
Предел последовательности
1. Основные сведения о числовых
последовательностях
Под числовой последовательностью
,
,
…,
,
… понимают функцию
,
заданную на множестве
- натуральных чисел. Числовая
последовательность обозначается
или
где
.
Последовательность задается формулой ее общего члена. Например,
:
1,
,
,
… ,
,
…
В школьном курсе математики изучаются арифметическая прогрессия
,
,
…,
,
…,
и геометрическая прогрессия
,
,
,
…,
,….
Последовательность называется
ограниченной, если существует такое
число
,
что для любого
выполняется неравенство
.
В противном случае, неограниченной. Так
последовательность
- ограничена, а последовательность
- неограниченна.
Последовательность
называется возрастающей (неубывающей),
если для любого
выполняются неравенства
,
аналогично убывающей (невозрастающей)
.
Такие последовательности называются
монотонными. Последовательность
:
не монотонна.
Если все члены последовательности
равны одному и тому же числу
,
то ее называют постоянной.
2. Предел числовой последовательности
Числовая последовательность
неограниченно приближается к единице.
В этом случае говорят, что последовательность
стремится к пределу равному
.
При этом абсолютная величина разности
становится все меньше и меньше, то есть
с ростом
модуль
будет меньше любого, сколь угодно малого
положительного числа.
Число
называется пределом последовательности
,
если для любого положительного числа
найдется такое натуральное число N,
что при всех
N
выполняется неравенство
.
В этом случае пишут,
и говорят, что последовательность имеет предел, равный . Также говорят, что последовательность сходится к . Последовательность не может иметь два различных предела.
Используя логические символы: квантор
общности
(для любого) и квантор существования
(найдется), символ равносильности
,
определение предела последовательности
можно коротко записать так.
(
N:
n>N
).
Г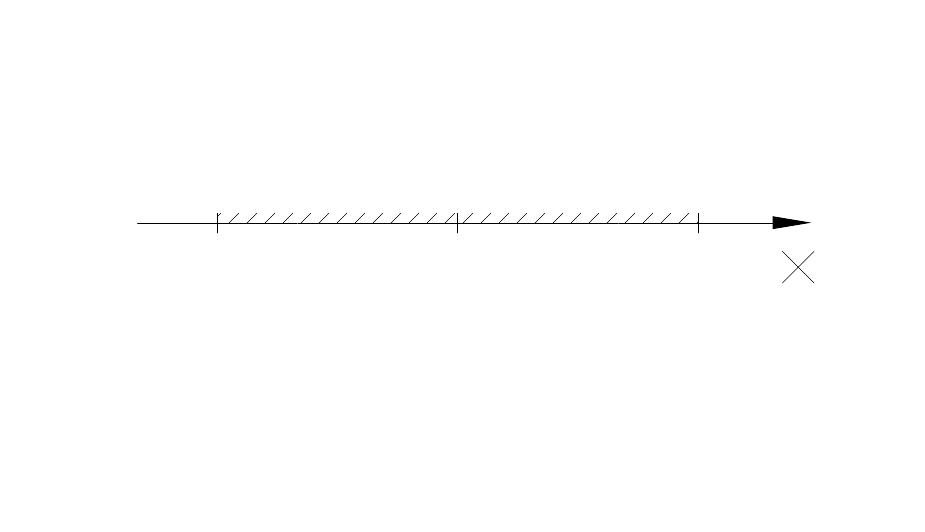
еометрический
смысл определения предела последовательности
состоит в следующем. Неравенство
равносильно неравенствам
или
,
которые показывают, что член
находится в
- окрестности точки
,
начиная с некоторого номера
.
Ясно, что чем меньше , тем больше число N , и в любом случае внутри - окрестности точки находится бесконечное число членов последовательности, а вне нее может быть, лишь конечное их число.
Последовательность, не имеющая предела,
называется расходящейся. Для постоянной
последовательности
.
Всякая монотонная ограниченная
последовательность имеет предел (теорема
Вейерштрасса).
3. Нахождение пределов числовых последовательностей. Число
Для вычисления пределов последовательностей
используют следующую теорему. Если
,
,
то
,
,
,
где
Например, найти пределы следующих последовательностей.
1.
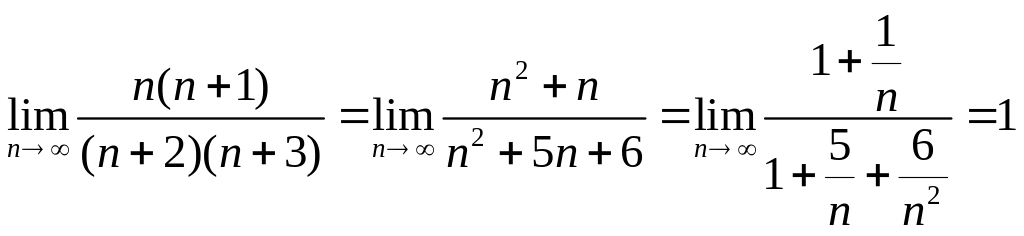(так как
при
).
2.
.
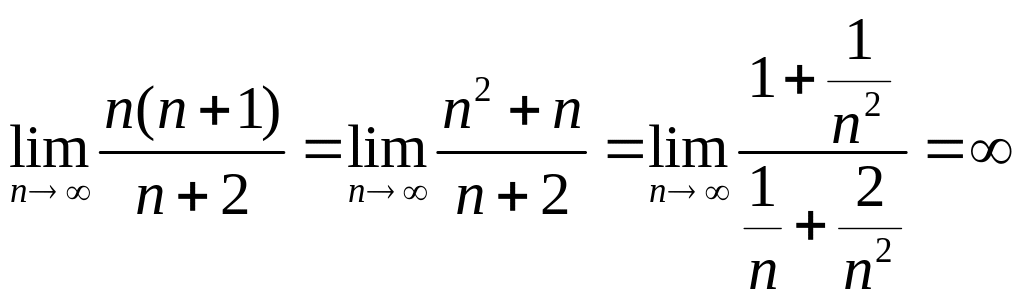3.
.
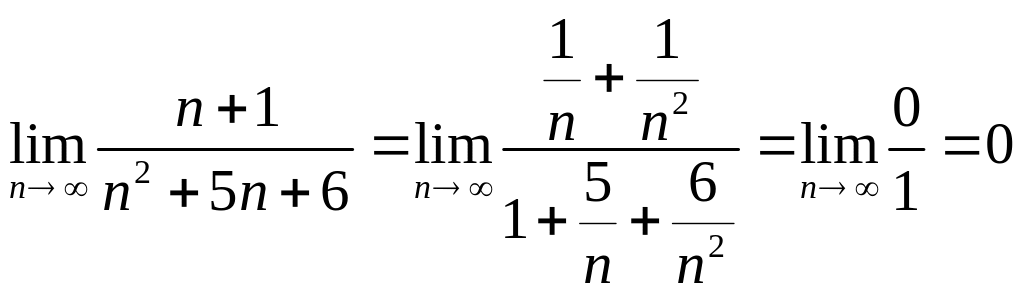4.
.
Последовательность с общим членом
имеет предел, обозначаемый обычно буквой
е, то есть
.
Число
иррациональное, его приближенное
значение равно 2,72 (е=2,718281828459045…).
Это
число играет важную роль в математике
и ее приложениях. График функции
получил название экспоненты. Широкое
применение имеет логарифм по основанию
,
называемый натуральным логарифмом
.
К числу
приводит анализ таких процессов, как
рост населения, размножение бактерий,
распад радиоактивных элементов.
В
экономике число
используется, например, в задаче о
непрерывном начислении процентов. Пусть
вклад в банк
денежных единиц и банк выплачивает
ежегодно
годовых. Найти размер вклада
через
лет. При использовании простых процентов
ежегодно вклад увеличивается на величину
,
то есть
.
В
финансовых расчетах возникает
необходимость применять сложные
проценты, когда размер вклада увеличивается
в одно и тоже число
раз, то есть
,
,
… ,
.
Если начислять проценты не один раз в год, а раз, то
.
Пусть они начисляются непрерывно (квартал, месяц, каждый день, час и так далее). Тогда
.
Эта формула при непрерывном начислении процентов, используется при анализе различных финансовых задач.