1. Методика построения матрицы дробного многофакторного эксперимента без дублирования опытов для исследования оперативно – тактических действий пожарных подразделений.

Дробные факторные планы (ДФП), как и полные факторные планы (ПФП), предназначены для построения математической модели объекта. При заданном числе факторов ДФП содержат меньшее число опытов по сравнению с ПФП. Но эта экономия достигается ценой упрощения математической модели.

Напомним, что по результатам ПФП 2^k можно оценить свободный член в математической модели, все линейные коэффициенты регрессии и все взаимодействия факторов. Однако во многих случаях учёт всех взаимодействий факторов не вызывается необходимостью. Так, при первоначальном изучении объектов широко применяются эксперименты с целью получения линейной модели. Для k варьируемых факторов такая модель имеет следующий вид: (12.1) и содержит (k + 1) коэффициент регрессии

(12.1)

Эксперимент, позволяющий отыскать эти коэффициенты, должен содержать не менее чем (k + 1) опытов. С точки зрения экономии средств, желательно, чтобы число опытов N не слишком превышало эту величину. С этой позиции ПФП при отыскании линейной модели неудовлетворительны. В силу соотношения N = 2^k число опытов ПФП существенно превосходит величину (k + 1), начиная уже с трёх факторов. Полные факторные планы неэкономичны, даже если экспериментатора интересуют помимо линейных коэффициентов регрессии некоторые (но не все) взаимодействия факторов.

Пусть, например, по результатам эксперимента с шестью факторами (k = 6) необходимо оценить свободный член, линейные коэффициенты регрессии и парные взаимодействия. Минимально необходимое для этого число опытов равно числу коэффициентов регрессии:

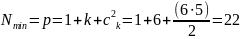(12.2)

в то время как ПФП 2^k шести факторов содержит N = 2⁶ = 64 опыта.

Дробные факторные планы позволяют сократить число опытов по сравнению с ПФП в случае, если в уравнении регрессии можно заранее пренебречь некоторыми взаимодействиями факторов. Для уяснения идеи построения дробных факторных планов обратимся сначала к плану ПФП 2² с двумя факторами (табл. 12.1).

Таблица12.1

Матрица базисных функций ПФП 2² для модели (12.2)

Собственно экспериментальным планом являются только столбцы 3 и 4 табл. 12.1. Столбец х₀ добавлен для вычисления коэффициента регрессии b₀, а столбец x₁х₂ - для вычисления коэффициента b₁₂ при произведении факторов x₁ и х₂. Следует отметить, что полученная матрица базисных функций удовлетворяет трём свойствам - (11.5) - (11.7). По результатам такого эксперимента можно получить модель в виде

(12.3)

Предположим теперь, что имеется объект с тремя варьируемыми факторами x₁, х₂, х₃, причём целью эксперимента является построение линейной модели, то есть имеются основания пренебречь всеми взаимодействиями факторов. В таком случае можно опять воспользоваться матрицей плана 2² в табл. 12.1. Потребуем, чтобы в этом эксперименте факторы x₁ и х₂ по-прежнему варьировались в соответствии с элементами столбцов 3 и 4, а фактор х₃ варьировался так же как и взаимодействие факторов x₁ х₂ (столбец 5 табл. 12.1.).

Таким образом, для эксперимента с тремя факторами получен план из четырёх опытов, по результатам которого можно построить линейную модель:

(12.4)

Перепишем матрицу этого плана в табл. 12.2

Таблица12.2

Планы такого типа называются дробными факторными планами (ДФП) или дробными репликами полных факторных планов. В частности, план, приведённый в табл. 12.2, называется полурепликой (или 1/2 реплики) от ПФП 2². Его обозначение 2^3-1 . Здесь 3 - число факторов, а единица вверху символизирует тот факт, что только одно взаимодействие заменяется новым фактором. Именно такие ДФП и называются полурепликами.

В ДФП 2^3-1фактор х₃ варьируется одинаково с парным взаимодействием x₁ х₂. Поэтому в уравнении регрессии нельзя отделить влияние фактора х₃ от влияния взаимодействия x₁ х₂. Если обозначить через β истинные величины соответствующих коэффициентов регрессии, то можно сказать, что коэффициент β₃ даёт совместную оценку двух истинных коэффициентов регрессии β ₃ и β₁₂ : b₃ → β ₃ + β₁₂ - это так называемая смешанная оценка.

Если построить столбцы х₁ х₃ и х₂ х₃, то легко убедиться, что они совпадут со столбцами х₂ и х₁ соответственно (рекомендуется проделать это самостоятельно). Следовательно, имеем дополнительно смешанные оценки:

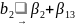(12.5)

(12.6)

При построении данной полуреплики2^3-1было использовано соотношение х₃ = х₁ х₂, которое называется генератором плана. Умножим обе его части на х₃: х₃₂= х₁ х₂ х₃. Но 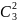= 1, так как нормализованный фактор х₃ в эксперименте равен либо +1, либо -1; следовательно, имеем 1 = х₁х₂ х₃.

Такое соотношение, в левой части которого стоит 1, а в правой - некоторое произведение факторов, называется определяющим контрастом (ОК) данной реплики. С помощью ОК легко определить систему смешивания оценок, не прибегая к построению дополнительных столбцов. Для этого обе части ОК умножаются поочерёдно на х₁ х₂ х₃. Получим х₁= х₂ х₃. Откуда следует:

(12.7)

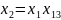(12.8)

откуда ;

Отметим, что, приравняв х₃ = - х₁ х₂, можно было получить другую полуреплику2^3-1. А обе эти полуреплики, взятые вместе, составят ПФП 2³.

Формулы для расчёта коэффициентов регрессии ПФП остаются полностью справедливыми и для ДФП.

Обратимся к построению дробных факторных планов на основе ПФП 2³. Матрица базисных функций этого плана приведена в табл. 12.3.

Таблица 12.3

Матрица базисных функций ПФП 2³

Имеется несколько способов построения полуреплики с четырьмя факторами на основе этого плана в зависимости от того, каким из взаимодействий решено пренебречь. Так, пренебрегая тройным взаимодействием х₁ х₂ х₃ и заменив соответствующий столбец фактором х₄, получим следующий план для четырёх факторов (одна из полуреплик2^4-1, табл. 12.4).

Для этого плана имеем генератор х₄= х₁х₂х₃. ОК равен 1 = х₁х₂х₃= х₄. Умножая OK последовательно на х₁, х₂, х₃, х₁х₂, х₁х₃, х₂х₃, получаем новые генераторы: х₁ = х₂х₃ х₄; х₂ = х₁ х₃ х₄; х₃ = х₁ х₂ х₄; х₁ х₂ = х₃ х₄; х₁ х₃ = х₂ х₄; х₂ х₃ = х₁ х₄.

В результате имеем следующую систему смешивания оценок:

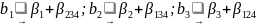
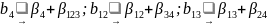
Таблица 12.4

ПФП 2^{4– 1}х₄= х₁х₂х₃

В уравнение регрессии, построенное по результатам реализации такого плана, можно включить, кроме линейных членов, все парные взаимодействия, приведённые в плане табл. 12.3:

(12.9)

Однако надо помнить о системе смешивания. К примеру, коэффициент b₁₂ оценивает не только при β ₁₂, но и β _34.

План в табл. 12.4, используемый для построения модели (12.9), является насыщенным, число опытов в нём N = 8 равно числу оцениваемых коэффициентов регрессии. Поэтому нет возможности проверить адекватность модели. Такую проверку можно сделать, если упростить уравнение (12.9), пренебрегая в нём дополнительно ещё некоторыми взаимодействиями.

Рассмотрим другой вариант полуреплики, приравняв, например, х₄ парному взаимодействию х₁ х₃. Этот план приведён в табл. 12.5.

ОК такой реплики: 1 = х ₁ х ₃ х ₄ . Генераторы плана: х ₁ = х ₃ х ₄ ;

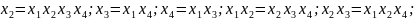
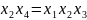
Таблица 12.5

ДФП 2^4-1х₄ = х₁х₃

Система смешивания оценок:

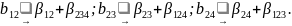
Сравнивая системы смешивания оценок для двух последних планов, можно убедиться в преимуществах плана с OK 1 = x₁ х₂х₃ х₄. Для него оценки линейных коэффициентов регрессии смешаны лишь с тройными взаимодействиями, в то время как для плана с OK 1 = x₁ х₃ х₄ некоторые из этих оценок смешаны с парными взаимодействиями. Отсюда следует вывод: с точки зрения системы смешивания оценок, лучше выбирать реплипки, в правой части ОК которых стоит максимальное число членов.

Кроме предложенных вариантов, можно рассмотреть ещё 6 способов построения полуреплик на основе ПФП 2³. Их генераторы:

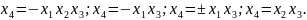
Идею построения ДФП можно развивать дальше, заменяя в планах ПФП не одно, а большее число взаимодействий новыми факторами. При замене двух взаимодействий новыми факторами получим четверть-реплики (или 1/4 реплики) ПФП. Их условное обозначение 2^{к- 2}.

В табл. 12.6 приведён план 1/4 реплики для 5 факторов, полученный заменой в ПФП 2³ взаимодействий x₁ х₂ х₃ и х₂ х₃ факторами х₄ и х₅ соответственно.

Таблица 12.6

ДФП 2^{5 - 2}

При замене в ПФП трёх взаимодействий новыми факторами получают 1/8 реплики ПФП, обозначаемые 2^к-3 и т. д.

На основе ПФП 2³ можно построить дробную реплику, включающую самое большее 7 варьируемых факторов. Это будет план 2^{7 - 4}, представляющий собой 1/16 реплики от ПФП 2³.

В табл. 12.7 приведён этот план, построенный с помощью следующих генераторов: x₄= x₁x₂; х₅ =x₁x₃ ; х₆ = х₂ х₃; х₇ = x₁x₂ x₃.

С помощью такого плана можно получить линейную модель

(12,10)

однако нельзя проверить адекватность такой модели, так как план 2^7-4 является насыщенным.

Насыщенные дробные факторные планы часто используют в качестве планов отсеивающего эксперимента, основная цель которых не построение адекватной модели, а выявление важнейших переменных из числа варьируемых факторов.

Таблица12.7

ДФП2^{7 - 4}